Java实现二叉搜索树的插入、删除

前置知识

二叉树的结构

    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }
    }

中序遍历

• 中序遍历：对于每一个节点，遍历顺序是：左子树->当前节点->右子树
• 中序遍历得到的第一个节点是没有左子树的（也许是叶子节点，也许有右子树）
• 同理，中序遍历的最后一个节点没有右子树

代码递归实现

    public void inorder_traversal(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left != null) {
            inorder_traversal(root.left);
        }
        System.out.println(root.val);
        if (root.right != null) {
            inorder_traversal(root.right);
        }
    }

二叉搜索树的定义

1. 左子树的所有节点大于当前节点
2. 右子树的所有节点小于当前节点
3. 每一个节点的值都不相同
4. 中序遍历的结果是升序的

这些定义决定了它的优点：查找效率快，因为二叉搜索树查找一个值时，自带二分查找的方式

下图就是一个标准的二叉搜索树

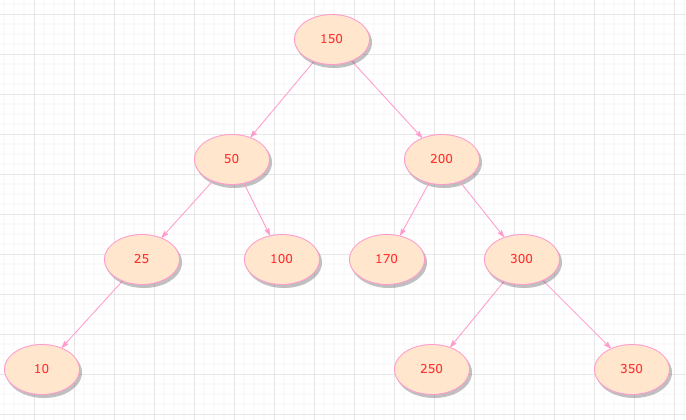
查找节点

给定一个值，使用循环在二叉搜索树中查找，找到该节点为止

1. 从根节点开始，进行比较
2. 给定值大于根节点就找右子树
3. 给定值小于根节点就找左子树

代码实现如下

public TreeNode search(TreeNode root, int val) {
        // 节点不为空，且不等于特定值
        while(root != null && root.val != val){
            if(root.val > val){
                root = root.left;
            }else{
                root = root.right;
            }
        }
        return root;
    }

添加节点

二叉搜索树的添加是将新的节点作为叶子节点加入到其中，因为叶子节点的增加比较简单。

1. 跟搜索过程类似，从根节点开始找，如果，如果小，找到一个适合新节点的位置
   1. 新节点的值比当前节点大（小），并且右（左）子树为空，插入到当前节点的右（左）子树中
   2. 如果当前节点的子树不为空，继续往下寻找
2. 然后使用一个pre节点，由pre节点作为父节点添加新节点

• 有可能要插入节点的二叉树是一颗空树，创建一个新的二叉树
• 如果新节点的值已经存在二叉树中，不需要进行添加

    public TreeNode insertInto(TreeNode root, int val) {

        if (root == null) {
            // 树为空树的情况
            return new TreeNode(val);
        }
        // 一个临时节点指向根节点，用于返回值
        TreeNode tmp = root;
        TreeNode pre = root;

        while (root != null && root.val != val) {
            // 保存父节点
            pre = root;
            if (val > root.val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        // 通过父节点添加
        if (val > pre.val) {
            pre.right = new TreeNode(val);
        } else {
            pre.left = new TreeNode(val);
        }
        return tmp;
    }

删除节点

二叉搜索树删除节点的过程比较复杂，因为被删除节点可能是以下三种情况

1. 叶子节点
2. 有一个子节点
3. 有两个子节点

删除叶子节点

直接搜索到相应的节点，然后删除，叶子节点的删除不影响树的性质

有一个子节点的节点

将节点删除，让父节点连接子节点即可，因为子节点与父节点的关系 = 当前节点与父节点的关系，并不改变树的性质

• 二叉搜索树的定义决定了：当前节点 大于（小于） 父节点，那么它的子节点 大于（小于） 父节点

过程像这张图一样

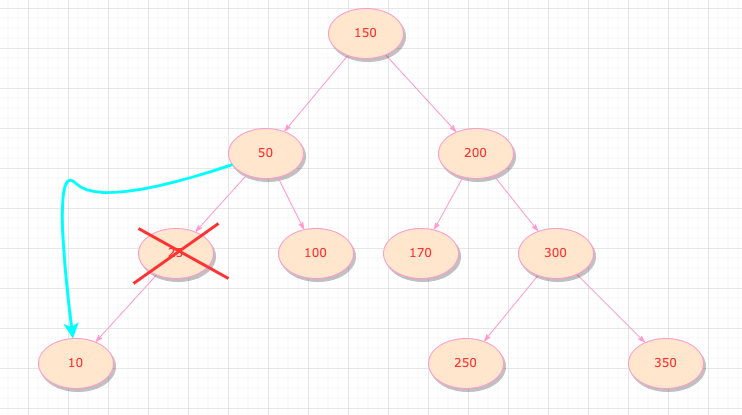
删除有两个子节点的节点

我们可以通过交换节点的方式，让要删除节点和只有一个子节点的节点交换，删除节点的操作就变成了上面的情况。

二叉搜索树中序遍历的结果是升序的，如果要交换，肯定要找中序遍历在该节点左右两边的节点（值交换之后也满足二叉搜索树的定义）

• 中序遍历的后（前）一个节点是右（左）子树中序遍历的第一个（最后一个）节点，而且它们都只有一个子节点

过程跟下面这张图类似（与中序遍历的后一个节点交换，并删除这个节点）

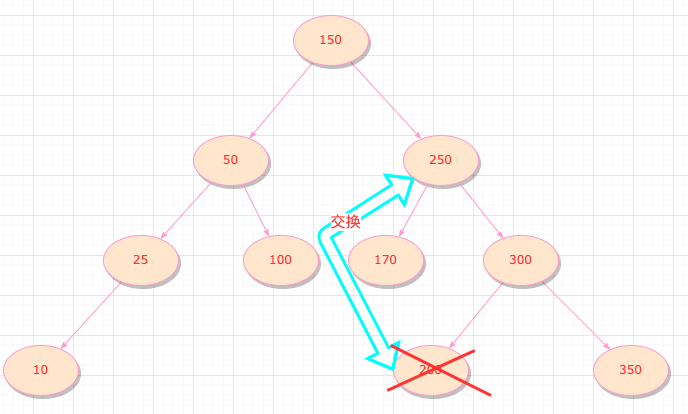
代码实现

public TreeNode deleteNode(TreeNode root, int key) {
        TreeNode tmp = root;

        TreeNode pre = root;

        // 寻找要删除的节点
        while (root != null && root.val != key) {
            pre = root;
            if (key > root.val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        // 找不到符合的节点值
        if (root == null) {
            return tmp;
        }

        // 只有一个子节点的情况
        if (root.left == null || root.right == null) {
            if (root.left == null) {
                // 要删除的是根节点，返回它的子节点
                if (root == tmp) {
                    return root.right;
                }
                // 使用父节点连接子节点，实现删除当前节点
                if (pre.left == root) {
                    pre.left = root.right;
                } else {
                    pre.right = root.right;
                }
            } else {
                if (root == tmp) {
                    return root.left;
                }
                if (pre.left == root) {
                    pre.left = root.left;
                } else {
                    pre.right = root.left;
                }
            }
            return tmp;
        }

        // 第一种方式
        // 寻找中序遍历的后一个节点，也就是右子树进行中序遍历的第一个节点，右子树的最左节点
        pre = root;
        TreeNode rootRight = root.right;
        while (rootRight.left != null) {
            pre = rootRight;
            rootRight = rootRight.left;
        }

        // 节点的值进行交换
        int tmpVal = rootRight.val;
        rootRight.val = root.val;
        root.val = tmpVal;

        // 中序遍历的第一个节点肯定是没有左子树的，但是可能有右子树，将右子树连接到父节点上（相当于删除有一个子节点的节点）
        if (pre.left == rootRight) {
            pre.left = rootRight.right;
        }else {
            pre.right = rootRight.right;
        }

        // 第二种方式
        // 寻找中序遍历的前一个节点，也就是左子树进行中序遍历的最后一个节点，左子树的最右节点
//        pre = root;
//        TreeNode rootLeft = root.left;
//        while (rootLeft.right != null){
//            pre = rootLeft;
//            rootLeft = rootLeft.right;
//        }
//
//        int tmpVal = rootLeft.val;
//        rootLeft.val = root.val;
//        root.val = tmpVal;
//
//        // 中序遍历的最后一个节点肯定是没有右子树的，但是可能有左子树，将左子树连接到父节点上（相当于删除有一个子节点的节点）
//        if (pre.left == rootLeft) {
//            pre.left = rootLeft.left;
//        }else {
//            pre.right = rootLeft.left;
//        }

        return tmp;
    }