数值分析：幂迭代和PageRank算法(Numpy实现)

1. 幂迭代算法（简称幂法）

(1) 占优特征值和占优特征向量

已知方阵\(\bm{A} \in \R^{n \times n}\), \(\bm{A}\)的占优特征值是比\(\bm{A}\)的其他特征值（的绝对值）都大的特征值\(\lambda\)，若这样的特征值存在，则与\(\lambda\)相关的特征向量我们称为占优特征向量。

(2) 占优特征值和占优特征向量的性质

如果一个向量反复与同一个矩阵相乘，那么该向量会被推向该矩阵的占优特征向量的方向。如下面这个例子所示：

import numpy as np
def prime_eigen(A, x, k):
    x_t = x.copy()
    for j in range(k):
        x_t = A.dot(x_t)
    return x_t
if __name__ == '__main__':
    A = np.array(
        [
            [1, 3],
            [2, 2]
        ]
    )
    x = np.array([-5, 5])
    k = 4
    r = prime_eigen(A, x, k)
    print(r)

该算法运行结果如下：

250, 260

为什么会出现这种情况呢？因为对\(\forall \bm{x} \in \R^{n}\)都可以表示为\(A\)所有特征向量的线性组合(假设所有特征向量张成\(\R^n\)空间)。我们设\(\bm{x}^{(0)} = (-5, 5)^T\)，则幂迭代的过程可以如下表示：

\[\begin{aligned}
& \bm{x}^{(1)} = \bm{A}\bm{x}^{(0)} = 4(1,1)^T - 2(-3, 2)^T\\
& \bm{x}^{(2)} = \bm{A}^2\bm{x}^{(0)} = 4^2(1, 1)^T + 2(-3, 2)^T\\
& ...\\
& \bm{x}^{(4)} = \bm{A}^4\bm{x}^{(0)} = 4^4(1, 1)^T + 2(-3, 2)^T = 256(1, 1)^T + 2(-3, 2)^T\\
\end{aligned} \tag{1}
\]

可以看出是和占优特征值对应的特征向量在多次计算后会占优。在这里4是最大的特征值，而计算就越来越接近占优特征向量\((1, 1)^T\)的方向。

不过这样重复与矩阵连乘和容易导致数值上溢，我们必须要在每步中对向量进行归一化。就这样，归一化和与矩阵\(\bm{A}\)的连乘构成了如下所示的幂迭代算法：

import numpy as np
def powerit(A, x, k):
    for j in range(k):
        # 每次迭代前先对上一轮的x进行归一化
        u = x/np.linalg.norm(x)
        # 计算本轮迭代未归一化的x
        x = A.dot(u)
        # 计算出本轮对应的特征值
        lam = u.dot(x)
    # 最后一次迭代得到的特征向量x需要归一化为u
    u = x / np.linalg.norm(x)
    return u, lam        

if __name__ == '__main__':
    A = np.array(
        [
            [1, 3],
            [2, 2]
        ]
    )
    x = np.array([-5, 5])
    k = 10
    # 返回占优特征值和对应的特征向量
    u, lam = powerit(A, x, k)
    print("占优的特征向量:\n", u)
    print("占优的特征值:\n", lam)

算法运行结果如下：

占优的特征向量:
 [0.70710341 0.70711015]
占优的特征值:
 3.9999809247674625

观察上面的代码，我们在第\(t\)轮迭代的第一行，得到的是归一化后的第\(t-1\)轮迭代的特征向量近似值\(\bm{u}^{(t-1)}\)（想一想，为什么），然后按照\(\bm{x}^{(t)} = \bm{A}\bm{u}^{(t-1)}\)计算出第\(t\)轮迭代未归一化的特征向量近似值\(\bm{x}^{(t)}\)，需要计算出第\(t\)轮迭代对应的特征值。这里我们我们直接直接运用了结论\(\lambda^{(t)} = (\bm{u}^{(t-1)})^T \bm{x^{(t)}}\)。该结论的推导如下：



证明

---

对于第\(t\)轮迭代，其中特征值的近似未\(\bm{\lambda}^{(t)}\)，我们想解特征方程

\[\bm{x^{(t-1)}} \cdot \lambda^{(t)} = \bm{A}\bm{x}^{(t-1)}
\tag{2}
\]

以得到第\(t\)轮迭代时该特征向量对应的特征值\(\lambda^{(t)}\)。我们采用最小二乘法求方程\((2)\)的近似解。我们可以写出该最小二乘问题的正规方程为

\[(\bm{x}^{(t-1)})^T\bm{x}^{(t-1)} \cdot \lambda^{(t-1)} = (\bm{x}^{(t-1)})^T (\bm{A}\bm{x}^{(t-1)})
\tag{3}
\]

然而我们可以写出该最小二乘问题的解为

\[\lambda^{(t)} = \frac{(\bm{x}^{(t-1)})^T\bm{A}\bm{x}^{(t-1)}}{(\bm{x}^{(t-1)})^T\bm{x}^{(t-1)}}
\tag{4}
\]

式子\((4)\)就是瑞利（Rayleigh）商。给定特征向量的近似，瑞利商式特征值的最优近似。又由归一化的定义有

\[\bm{u}^{(t-1)} = \frac{\bm{x}^{(t-1)}}{||\bm{x}^{(t-1)}||} = \frac{\bm{x}^{(t-1)}}{{[(\bm{x}^{(t-1)})^T\bm{x}^{(t-1)}]}^{\frac{1}{2}}}
\tag{5}
\]

则我们可以将式\((4)\)写作：

\[\lambda^{(t)} = (\bm{u}^{(t-1)})^T\bm{A}\bm{u}^{(t-1)}
\tag{6}
\]

又因为前面已经计算出\(\bm{x}^{(t)} = \bm{A} \bm{u}^{(t-1)}\)，为了避免重复计算，我们将\(\bm{x}^{(t)}\)代入式\((5)\)得到：

\[\lambda^{(t)} = (\bm{u}^{(t-1)})^T\bm{x}^{(t)}
\tag{7}
\]

证毕。

---

可以看出，幂迭代本质上每步进行归一化的不动点迭代。

2. 逆向幂迭代

上面我们的幂迭代算法用于求解（绝对值）最大的特征值。那么如何求最小的特征值呢？我们只需要将幂迭代用于矩阵的逆即可。

我们有结论，矩阵\(\bm{A}^{-1}\)的最大特征值就是矩阵\(\bm{A}\)的最小特征值的倒数。事实上，对矩阵\(\bm{A} \in \R^{n \times n}\) ,令其特征值表示为\(\lambda_1, \lambda_2, ..., \lambda_n\)，如果其逆矩阵存在，则逆矩阵\(A\)的特征值为\(\lambda_1^{-1}, \lambda_2^{-1}, ..., \lambda_n^{-1}\), 特征向量和矩阵\(A\)相同。该定理证明如下：



证明

---

有特征值和特征向量定义有

\[\bm{A}\bm{v} = \lambda \bm{v}
\tag{8}
\]

这蕴含着

\[\bm{v} = \lambda \bm{A}^{-1}\bm{v}
\tag{9}
\]

因而

\[\bm{A}^{-1}\bm{v} = \lambda^{-1}\bm{v}
\tag{10}
\]

得证。

---

对逆矩阵\(\bm{A}^{-1}\)使用幂迭代，并对所得到的的\(\bm{A}^{-1}\)的特征值求倒数，就能得到矩阵\(\bm{A}\)的最小特征值。幂迭代式子如下：

\[\bm{x}^{(t+1)} = \bm{A}^{-1}\bm{x}^{(t)}
\tag{11}
\]

但这要求我们对矩阵\(\bm{A}\)求逆，当矩阵\(\bm{A}\)过大时计算复杂度过高。于是我们需要稍作修改，对式\((11)\)的计算等价于

\[\bm{A}\bm{x}^{(t+1)} = \bm{x}^{(t)}
\tag{12}
\]

这样，我们就可以采用高斯消元对\(\bm{x}^{(t+1)}\)进行求解，

不过，我们现在这个算法用于找出矩阵最大和最小的特征值，如何找出其他特征值呢？

如果我们要找出矩阵\(\bm{A}\)在实数\(s\)附近的特征值，可以对矩阵做出接近特征值的移动。我们有定理：对于矩阵\(\bm{A} \in \R^{n \times n}\)，设其特征值为\(\lambda_1, \lambda_2, ..., \lambda_n\)，则其转移矩阵\(\bm{A}-sI\)的特征值为\(\lambda_1 -s, \lambda_2 -s, ..., \lambda_n -s\)，而特征向量和矩阵\(A\)相同。该定理证明如下：



证明

---

有特征值和特征向量定义有

\[\bm{A}\bm{v} = \lambda \bm{v}
\tag{13}
\]

从两侧减去\(sI\bm{v}\)，得到

\[(\bm{A} - sI)\bm{v} = (\lambda - s)\bm{v}
\tag{14}
\]

因而矩阵\(\bm{A} - sI\)的特征值为\(\lambda - s\)，特征向量仍然为\(\bm{v}\)，得证。

---

这样，我们想求矩阵\(\bm{A}\)在实数\(s\)附近的特征值，可以先对矩阵\((\bm{A}-sI)^{-1}\)使用幂迭代求出\((\bm{A}-sI)^{-1}\)的最大特征值\(b\)（因为我们知道转移后的特征值为\((\lambda - s)^{-1}\)，要使\(\lambda\)尽可能接近\(s\)，就得取最大的特征值），其中每一步的\(x^{(t)}\)可以对\((\bm{A}-sI)\bm{x}^{(t)}=\bm{u}^{(t-1)}\)进行高斯消元得到。最后，我们计算出\(\lambda = b^{-1} + s\)即为矩阵\(A\)在\(s\)附近的特征值。该算法的实现如下：

import numpy as np

def powerit(A, x, s, k):
    As = A-s*np.eye(A.shape[0])
    for j in range(k):
        # 为了让数据不失去控制
        # 每次迭代前先对x进行归一化
        u = x/np.linalg.norm(x)

        # 求解(A-sI)xj = uj-1
        x = np.linalg.solve(As, u)
        lam = u.dot(x)
    lam = 1/lam + s

    # 最后一次迭代得到的特征向量x需要归一化为u
    u = x / np.linalg.norm(x)
    return u, lam        

if __name__ == '__main__':
    A = np.array(
        [
            [1, 3],
            [2, 2]
        ]
    )
    x = np.array([-5, 5])
    k = 10
    # 逆向幂迭代的平移值，可以通过平移值收敛到不同的特征值
    s = 2
    # 返回占优特征值和对应的特征值
    u, lam = powerit(A, x, s, k)
    # u为 [0.70710341 0.70711015]，指向特征向量[1, 1]的方向
    print("占优的特征向量:\n", u)
    print("占优的特征值:\n", lam)

算法运行结果如下：

占优的特征向量:
 [0.64221793 0.7665221 ]
占优的特征值:
 4.145795530352381

3. 幂迭代的应用：PageRank算法

幂迭代的一大应用就是PageRank算法。PageRank算法作用在有向图上的迭代算法，收敛后可以给每个节点赋一个表示重要性程度的值，该值越大表示节点在图中显得越重要。

比如，给定以下有向图：



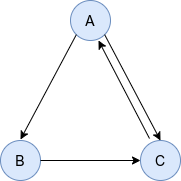
其邻接矩阵为：

\[\left(
\begin{matrix}
0 & 1 & 1 \\
0 & 0 & 1 \\
1 & 0 & 0 \\
\end{matrix}
\right)
\tag{15}
\]

我们将邻接矩阵沿着行归一化，就得到了马尔可夫概率转移矩阵\(\bm{M}\)：

\[\left(
\begin{matrix}
0 & \frac{1}{2} & \frac{1}{2} \\
0 & 0 & 1 \\
1 & 0 & 0 \\
\end{matrix}
\tag{16}
\right)
\]

我们定义上网者从一个页面转移到另一个随机页面的概率是\(q\)，停留在本页面的概率是\(1-q\)。设图的节点数为\(n\)，然后我们可以计算Google矩阵做为有向图的一般转移矩阵。对矩阵每个元素而言，我们有：

\[\bm{G}_{ij} = \frac{q}{n} + (1-q)\bm{M}_{ij}
\tag{17}
\]

注意，Google矩阵每一列求和为1，这是一个随机矩阵，它满足一个性质，即占优特征值为1.

我们采用矩阵表示形式，即：

\[\bm{G}_{ij} = \frac{q}{n}\bm{E} + (1-q)\bm{M}_{ij}
\tag{18}
\]

其中\(\bm{E}\)为元素全为1的\(n \times n\)方阵。

然后我们定义向量\(\bm{p}\)，其元素\(\bm{p}_i\)是待在页面\(i\)上的概率。我们由前面的幂迭代算法知道，矩阵与向量重复相乘后向量会被推到特征值为1的方向。而这里，与特征值１对应的特征向量是一组页面的稳态概率，根据定义这就是\(i\)个页面的等级，即PageRank算法名字中的Rank的由来。（同时，这也是\(G^T\)定义的马尔科夫过程的稳态解)。故我们定义迭代过程：

\[\bm{p}_{t+1} = \bm{G}^T\bm{p}_{t}
\tag{19}
\]

注意，每轮迭代后我们要对\(\bm{p}\)向量归一化（为了减少时间复杂度我们除以\(p\)向量所有维度元素中的最大值即可，以近似二范数归一化）；而且，我们在所有轮次的迭代结束后也要对\(p\)向量进行归一化（除以所有维度元素之和以保证所有维度之和为1）。

我们对该图的PageRank算法代码实现如下(其中移动到一个随机页面的概率\(q\)按惯例取0.15)：

import numpy as np
# 归一化同时迭代，k是迭代步数
# 欲推往A特征值的方向，A肯定是方阵
def PageRank(A, p, k, q):
    assert(A.shape[0]==A.shape[1])
    n = A.shape[0]
    M = A.copy().astype(np.float32) #注意要转为浮点型
    for i in range(n):
        M[i, :] = M[i, :]/np.sum(M[i, :])
    G = (q/n)*np.ones((n,n)) + (1-q)*M
    G_T = G.T
    p_t = p.copy()
    for i in range(k):
        y = G_T.dot(p_t)
        p_t = y/np.max(y)
    return p_t/np.sum(p_t)
if __name__ == '__main__':
    A = np.array(
        [
            [0, 1, 1],
            [0, 0, 1],
            [1, 0, 0]
        ]
    )
    k = 20
    p = np.array([1, 1, 1])
    q = 0.15 #移动到一个随机页面概率通常为0.15
    # 概率为1-q移动到与本页面链接的页面
    R= PageRank(A, p, k, q)
    print(R)

该算法运行结果如下：

[0.38779177 0.21480614 0.39740209]

可以看到20步迭代结束后网页的Rank向量\(\bm{R}=(0.38779177, 0.21480614, 0.39740209)^T\)，这也可以看做网页的重要性程度。

知名程序库和源码阅读建议

PageRank算法有很多优秀的开源实现，这里推荐几个项目：

(1) Spark-GraphX

GraphX是一个优秀的分布式图计算库，从属于Spark分布式计算框架，采用Scala语言实现了很多分布式的图计算算法，也包括我们这里所讲的PageRank算法。

文档地址：https://spark.apache.org/graphx

源码地址：https://github.com/apache/spark

(2) neo4j

neo4j是一个采用Java实现的知名的图数据库，该数据库也提供了PageRank算法的实现。

文档地址：https://neo4j.com/

源码地址：https://github.com/neo4j/neo4j.git

(3) elastic-search

如果你有兴趣深入研究搜索引擎的实现，那么向你推荐elastic-search项目，它是基于Java实现的一个搜索引擎。

文档地址：https://www.elastic.co/cn/

源码地址：https://github.com/elastic/elasticsearch.git

参考文献

• [1] Timothy sauer. 数值分析(第2版)[M].机械工业出版社, 2018.
• [2] 李航. 统计学习方法(第2版)[M]. 清华大学出版社, 2019.