带你理解MST性质

写在前面

最小生成树的引出

假设要在n个城市之间建立通信联络网，则连通n个城市需要n-1条线路。在这种情况下，我们自然需要考虑一个问题，如何在最节省经费的条件下建立这个网络？

很自然地我们会想到，将各个城市之间的线路开销转化为权重，要想找到最节省经费的方案，就需要找到能够连通所有城市且权重最小的连通线路。

因此，我们需要选择一颗生成树，使得该生成树总耗费最小，也就是用最小的代价构建这条连通网。我们称这样的网络为：最小代价生成树（简称：最小生成树）。

本文结构

本文从MST性质的定义和证明方面为读者解度最小生成树两个常见算法的前置理论性质。

普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法都是利用了MST性质的算法

建议读者在在理解了普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法之后再阅读此文

利用得到的最小生成树在回过头来理解MST会更加简单。

MST性质

MST性质的定义

假设N=(V,{E})是一个连通网，U是顶点集V的一个非空子集。

若(u,v)是一条既有最小权值(代价)的边，其中u∈U，v∈V，则必存在一颗包含边(u,v)的最小生成树。

证明

证明方法

可以用反证法证明。假设网N的任何一颗最小生成树都不包含(u,v)。设T是连通网上的一颗最小生成树，当将边(u,v)加入到T中时，由生成树的定义，T中必存在一条包含(u,v)的回路。

另一方面，由于T是生成树，则在T上必存在另外一条(u',v')，其中u'∈U，v'∈V-U，且u与u',v与v'均有路径相通。

删去边(u',v')即可消除上述回路，同时得到另外一颗生成树T'。因为(u,v)的代价不高于(u'v')，则T'的代价亦不高于T，T'是一颗包含(u,v)的最小生成树。与假设假设矛盾。

举个例子

现在，给出一个连通图：

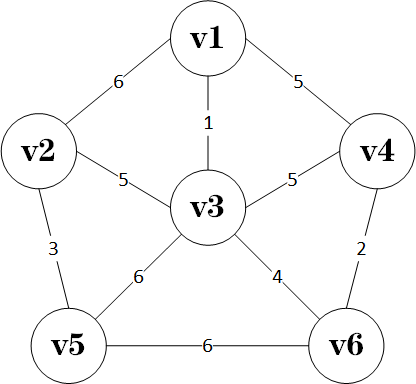
众所周知，这样一给连通网的最小生成树为：

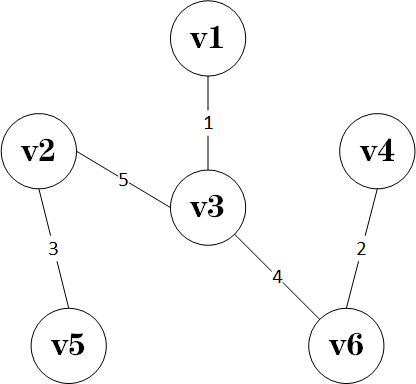
那么可以按照如下方式对MST进行证明：