noip38

T1

有个朴素的暴力，枚举每一个子矩形，复杂度 \(O(n^{2}m^{2})\)，观察数据范围，n很小，考虑枚举行，对于 \(m\) 用 \(two\;pointers\) 来维护。

先预处理出每一列的前缀和，然后枚举行，对于列，用个双指针，把 \([l,r]\) 这一段区间卡出来，答案每回累加合法的区间长度即可。

复杂度 \(O(n^{2}m)\)

Code

#include<cmath>
#include<cstdio>
#define MAX 50100
#define re register
#define int long long
namespace OMA
{
	char ch[MAX];
	int n,m,l,r,tot[MAX];
	int ans,sum[33][MAX];
	struct stream
	{
		template<typename type>inline stream &operator >>(type &s)
		{
			int w=1; s=0; char ch=getchar();
			while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
			while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
			return s*=w,*this;
		}
	}cin;
	signed main()
	{
		//freopen("node.in","r",stdin);
		cin >> n >> m;
		for(re int i=1; i<=n; i++)
		{
			scanf("%s",ch+1);
			for(re int j=1; j<=m; j++)
			{ sum[i][j] = sum[i-1][j]+(ch[j]=='1'); }
		}
		cin >> l >> r;
		for(re int i=1; i<=n; i++)
		{
			for(re int j=i; j<=n; j++)
			{
				int lp = 0,rp = 0;
				for(re int k=1; k<=m; k++)
				{
					//printf("i=%lld j=%lld k=%lld ",i,j,k);
					tot[k] = tot[k-1]+sum[j][k]-sum[i-1][k];
					//printf("tot[%lld]=%lld\n",k,tot[k]);
					while(tot[k]-tot[lp]>r&&lp+1<k)
					{ lp++; }
					while(tot[k]-tot[rp+1]>=l&&rp+1<k)
					{ rp++; }
					if(tot[k]-tot[rp]>=l)
					{ ans += rp-lp+1; }
				}
			}
		}
		printf("%lld\n",ans);
		return 0;
	}
}
signed main()
{ return (OMA::main(),0); }

T2

题意转换

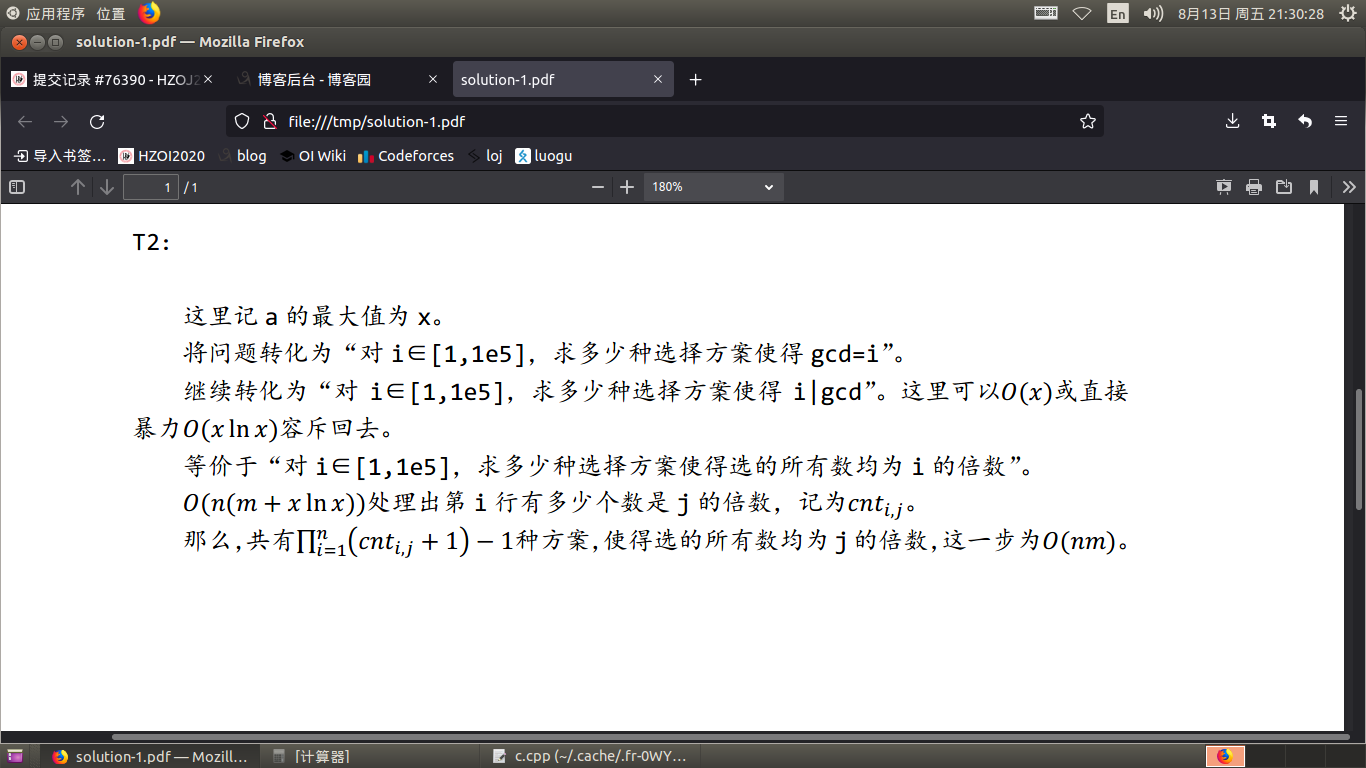
好了，现在你已经知道转换后的题意，问题在于如何求解 \(cnt\) 数组和答案。

对于每一行，我们都开一个桶记录 \(a\) 出现的次数。

然后枚举每一行，再从1枚举到最大值，再枚举当前枚举的数的倍数，加上上边说的桶即可 建议看code

这样得到的 \(cnt_{i,j}\) 表示第i行有多少个数为j的倍数，每一行求和就是总的，而我们要的是j，所以考虑一波容斥，即减去j的其他倍数即可，这样的话就要倒序枚举最大值。

复杂度 \(O(n(m+\max\{a\}\ln\max\{a\}))\) 。

Code

#include<cstdio>
#define MAX 100010
#define re register
#define int long long
const int N = 22;
namespace OMA
{
	int n,m,xam,ans;
	int a[N][MAX];
	int buc[N][MAX];
	int cnt[N][MAX],sum[MAX];
	const int p = 1e9+7;
	struct stream
	{
		template<typename type>inline stream &operator >> (type &s)
		{
			int w=1; s=0; char ch=getchar();
			while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
			while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
			return s*=w,*this;
		}
	}cin;
	inline int max(int a,int b)
	{ return a>b?a:b; }
	signed main()
	{
		cin >> n >> m;
		for(re int i=1; i<=n; i++)
		{
			for(re int j=1; j<=m; j++)
			{ cin >> a[i][j]; xam = max(xam,a[i][j]); buc[i][a[i][j]]++; }
		}
		for(re int i=1; i<=n; i++)
		{
			for(re int j=1; j<=xam; j++)
			{
				for(re int k=1; j*k<=xam; k++)
				{ cnt[i][j] += buc[i][j*k]; }
			}
		}
		/*for(re int i=1; i<=n; i++)
		{
			for(re int j=1; j<=xam; j++)
			{ printf("%lld ",cnt[i][j]); }
			printf("\n");
		}*/
		for(re int j=xam; j; j--)
		{
			sum[j] = 1;
			for(re int i=1; i<=n; i++)
			{ (sum[j] *= cnt[i][j]+1) %= p; }
			sum[j] -= 1;
			if(!sum[j])
			{ continue ; }
			for(re int k=2; k*j<=xam; k++)
			{ sum[j] -= sum[k*j]; }
			(ans += j*sum[j]) %= p;
		}
		printf("%lld\n",(ans+p)%p);
		return 0;
	}
}
signed main()
{ return OMA::main(); }

T3

点分治，不会，爬了