广度优先搜索（BreadthFirstSearch）& 迪克斯特拉算法 （Dijkstra's algorithm）

BFS可回答两类问题：

1.从节点A出发，有前往节点B的路径吗？

2.从节点A出发，前往节点B的哪条路径经过的节点最少？

BFS中会用到“队列”的概念。队列是一种先进先出（FIFO, first in first out）的数据结构，与栈不同，栈是后进先出（LIFO, last in first out）的数据结构。

还会用到“字典”的概念。字典在现在很多语言中都存在且广泛使用，字典中的元素是一组<键（key），值（value）>对，key的值是不可以重复的。关于字典的详细内容，网上有很多资料可以查阅。

问题描述：想从你的朋友中找出一个芒果销售商，如果你的朋友中没有，那么就从朋友的朋友中查找。（这里假设名字最后一个字母为“m”的即为芒果销售商）。这样就是从“you”这个节点出发，是否有到“Xm”这个节点的路径的问题。

思路：先从你的朋友开始查找，如果朋友A是芒果销售商，则程序结束，如果不是，则将A的朋友排到队列中。然后检查朋友B是否为芒果销售商，循环，直到找到芒果销售商或者队列中的朋友们都被检查了一遍。因为会有某个人C既是A的朋友又是B的朋友，而C只需要检查一次，因此要分配一个列表用于记录已经检查过哪些朋友了。

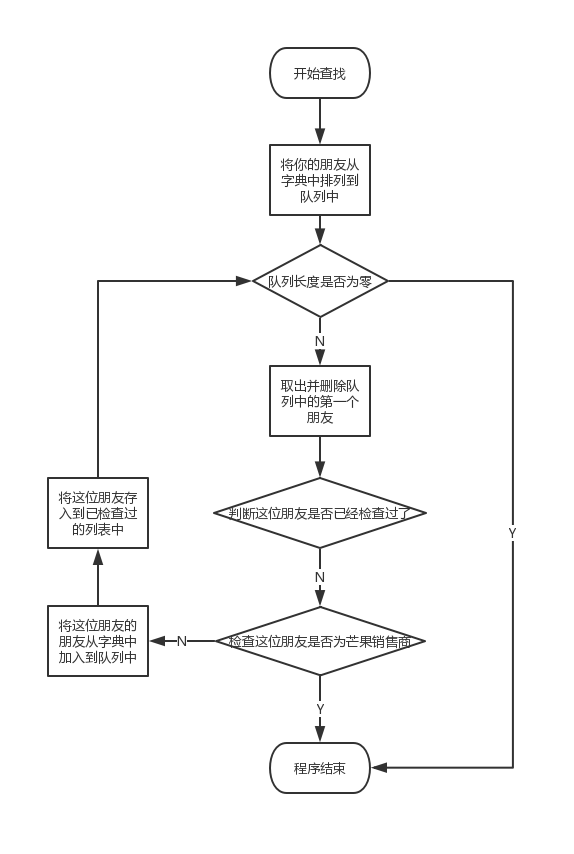
Python代码：

>>> from collections import deque

>>> graph = {}
>>> graph["you"]=["alice","bob","claire"]
>>> graph["bob"] = ["anuj","peggy"]
>>> graph["alice"] = ["peggy"]
>>> graph["claire"]=["thom","jonny"]
>>> graph["anuj"]=[]
>>> graph["peggy"]=[]
>>> graph["thom"]=[]
>>> graph["jonny"]=[]

>>> def search(name):
    search_queue = deque()
    search_queue += graph[name]
    searched = []
    while search_queue:
        person = search_queue.popleft()
        if person not in searched:
            if person_is_seller(person):
                print (person + " is a mango seller!")
                return True
            else:
                search_queue += graph[person]
                searched.append(person)
    return False

>>> def person_is_seller(name):
    return name[-1] == 'm'

>>> search("you")
thom is a mango seller!
True

C#代码：

namespace Algorithms
{
    public static class BFS
    {
        public static bool BreadthFirstSearch(string name, Dictionary<string,List<string>>graph)
        {
            Queue<string> search_queue = new Queue<string>();
            foreach (var item in graph[name])
                search_queue.Enqueue(item);
            List<string> searched = new List<string>();
            while (search_queue.Count != 0)
            {
                string person = search_queue.Dequeue();
                if (!searched.Contains(person))
                {
                    if (JudgeSeller(person))
                    {
                        Console.WriteLine(person + " is a mango seller!");
                        return true;
                    }
                    else
                    {
                        foreach (var item in graph[person])
                            search_queue.Enqueue(item);
                        searched.Add(person);
                    }
                }
            }
            return false;
        }
        private static bool JudgeSeller(string name)
        {
            if (name[name.Length - 1] == 'm')
                return true;
            return false;
        }
    }
}

测试：

namespace Algorithms
{
    class Program
    {
        static void Main(string[] args)
        {
            Dictionary<string, List<string>> graph = new Dictionary<string, List<string>>();
            graph["you"] = new List<string>() { "alice", "bob", "claire" };
            graph["alice"] = new List<string>() { "peggy" };
            graph["bob"] = new List<string>() { "anuj", "peggy" };
            graph["claire"] = new List<string>() { "thom", "jonny" };
            graph["anuj"] = new List<string>();
            graph["peggy"] = new List<string>();
            graph["thom"] = new List<string>();
            graph["jonny"] = new List<string>();

            if (!BFS.BreadthFirstSearch("you", graph))
            {
                Console.WriteLine("no mango seller!");
            }
            Console.Read();
        }
    }
}

Dijkstra's algorithm 用于计算出最短路径，但是这个算法在使用上有很多限制条件。

问题描述：从A地到B地的各种可能的路径中，哪条路径所用的时间最短。（图中的数字表示从某地到另外某地所用的时间）

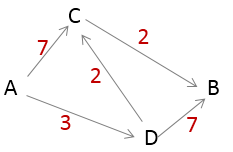
图1

思路：记录从A点到其他各个节点的所需的时间，如表1所示（现在还不知道从A到B的时间，则先设置为无穷大）

D	3
C	7
B	∞

表1

从所需时间最短的D点再出发，计算从A经过D到其他个各节点的时间，如表2所示

C	5
B	10

表2

直接前往C点需要的时间为7，而经过D点前往C点所需的时间为5，时间缩短了，则更新从A到各个点所需的时间的列表，如表3所示

D	3
C	5
B	10

表3

现在除了节点D之外，从A到C的时间是最短的了，则计算从A经过C再到其他节点的时间，如表4所示。

B

7

表4

现在从A经过D再经过C然后到B的时间为7，小于表3记录的到B的时间，则更新这个时间。

就这样得到了花费时间最短的路径。总结一下就是，不断的获得从起点到某点的最短时间，然后更新这个时间列表。在 Dijkstra's algorithm中，这些数字被称为“权重（weight）”，而带权重的图则被称为加权图（weighted graph），那么不带权重的则被称为非加权图（unweighted graph）。对于计算非加权图中的最短路径，可使用BFS，计算加权图中的最短路径，可使用 Dijkstra's algorithm。然而， Dijkstra's algorithm不适用于带环的图，即图1中的箭头如果是双向的话那么就是不适用的。此外，它还不适用于带有负权重的情况。

Dijkstra算法的实现需要使用三个散列表。第一个散列表记录的是每个点的邻居及权重。第二个散列表记录的是从起点开始到每个节点的权重，第三个散列表记录的是各个节点父节点。

Python代码：

#第一个散列表，记录每个点的邻居及权重
graph={}
graph["A"]={}
graph["A"]["C"]=7
graph["A"]["D"]=3
graph["C"]={}
graph["C"]["B"]=2
graph["D"]={}
graph["D"]["C"]=2
graph["D"]["B"]=7
graph["B"]={}

#第二个散列表，记录从起点A到其他各个节点的权重
#由于节点B不是A的邻居，则A到B的权重暂设置为无穷大
costs={}
infinity = float("inf")
costs["C"]=7
costs["D"]=3
costs["B"]=infinity

#第三个散列表，用于存储节点的父节点
parents={}
parents["C"]="A"
parents["D"]="A"
parents["B"]=None

#用于记录已经处理过的节点的数组
processed=[]

#先在未处理的节点数组中找到权重最小的节点
def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs:
        cost = costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node

node = find_lowest_cost_node(costs)
while node is not None:
    cost = costs[node]
    neighbors=graph[node]
    for n in neighbors.keys():
        new_cost=cost + neighbors[n]
        if costs[n] > new_cost:
            costs[n] = new_cost
            parents[n]=node
    processed.append(node)
    node=find_lowest_cost_node(costs)

for node in costs:
    print("Node:" + node+ "  Cost:" + str(costs[node]) + "\r\n")

for node in parents:
    print("ChildNode:" + node + " ParentNode:" + parents[node] + "\r\n")

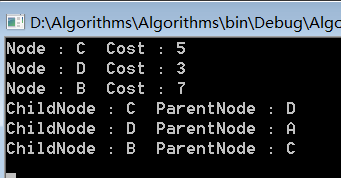
运行结果：

Node:C  Cost:5

Node:D  Cost:3

Node:B  Cost:7

ChildNode:C ParentNode:D

ChildNode:D ParentNode:A

ChildNode:B ParentNode:C

>>> 

C#代码：

public class DijkstraAlgorithm
    {
        public Dictionary<string, double> Costs { get; set; }
        public Dictionary<string, string> Parents { get; set; }
        public Dictionary<string, Dictionary<string,double>> Graph { get; set; }
        private List<string> processed = new List<string>();
        public DijkstraAlgorithm()
        {
            Costs = new Dictionary<string, double>();
            Parents = new Dictionary<string, string>();
            Graph = new Dictionary<string, Dictionary<string, double>>();
        }

        public void Dijkstra_Algorithm()
        {
            string node = FindLowestCostNode();
            while(node != null)
            {
                double cost = Costs[node];
                Dictionary<string, double> neighbors = Graph[node];
                foreach(KeyValuePair<string,double> item in neighbors)
                {
                    double new_cost = cost + item.Value;
                    if (Costs[item.Key] > new_cost)
                    {
                        Costs[item.Key] = new_cost;
                        Parents[item.Key] = node;
                    }
                }
                processed.Add(node);
                node = FindLowestCostNode();
            }
        }
        private string FindLowestCostNode()
        {
            string lowestcostnode = null;
            double lowestcost = double.PositiveInfinity;
            foreach(KeyValuePair<string,double> item in Costs)
            {
                if(item.Value < lowestcost && !processed.Contains(item.Key))
                {
                    lowestcost = item.Value;
                    lowestcostnode = item.Key;
                }
            }
            return lowestcostnode;
        }

    }

字典的初始化以及运行结果：

DijkstraAlgorithm Dalgorithm = new DijkstraAlgorithm();
            Dalgorithm.Graph["A"] = new Dictionary<string, double>();

            Dalgorithm.Graph["A"]["C"] = 7;
            Dalgorithm.Graph["A"]["D"] = 3;

            Dalgorithm.Graph["C"] = new Dictionary<string, double>();
            Dalgorithm.Graph["C"]["B"] = 2;
            Dalgorithm.Graph["D"] = new Dictionary<string, double>();
            Dalgorithm.Graph["D"]["C"] = 2;
            Dalgorithm.Graph["D"]["B"] = 7;

            Dalgorithm.Graph["B"] = new Dictionary<string, double>();

            Dalgorithm.Costs["C"] = 7;
            Dalgorithm.Costs["D"] = 3;
            Dalgorithm.Costs["B"] = double.PositiveInfinity;

            Dalgorithm.Parents["C"] = "A";
            Dalgorithm.Parents["D"] = "A";
            Dalgorithm.Parents["B"] = null;

            Dalgorithm.Dijkstra_Algorithm();

            foreach(KeyValuePair<string,double> item in Dalgorithm.Costs)
            {
                Console.WriteLine("Key : " + item.Key + "  Value : " + item.Value);
            }

            foreach(KeyValuePair<string,string> item in Dalgorithm.Parents)
                Console.WriteLine("Key : " + item.Key + "  Value : " + item.Value);

            Console.Read();