ECDSA—模逆模块

在有限域F_p上的非零元素a的逆记为a^-1mod p 。即在有限域F_p上存在唯一的一个元素x，使得ax恒等于1（mod p），则元素x为a的逆a^-1 。本次设计采用扩展的整数Euclidean算法来求逆元。

扩展的整数Euclidean算法可参考该网站：https://www.cnblogs.com/GjqDream/p/11537934.html

本博文主要介绍verilog实现该算法。

根据模块化的设计思想，设计该模块接口定义如下：

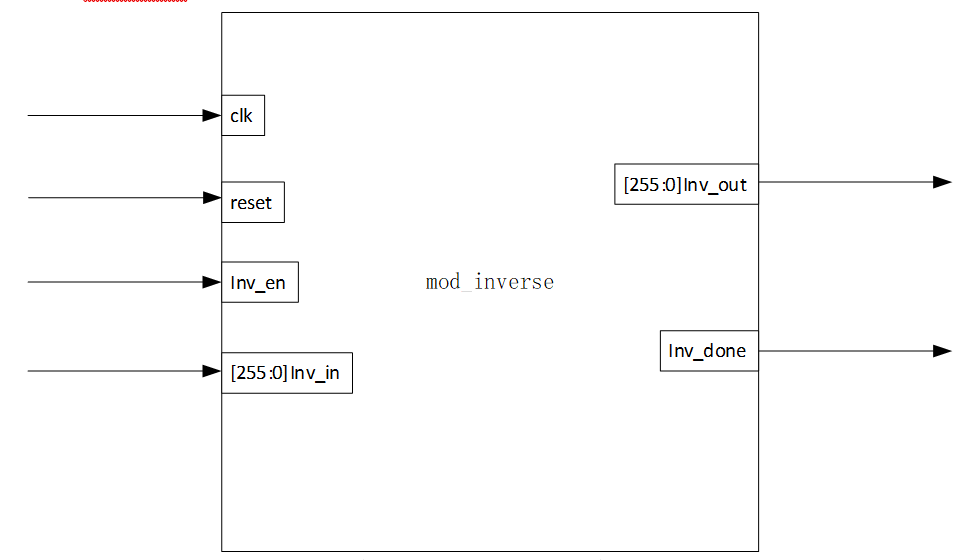
信号名	方向	位宽	端口定义
clk	Input	1	时钟
reset	Input	1	复位
Inv_en	Input	1	模逆使能信号
Inv_in	Input	512	待求逆信号
Inv_out	output	256	模逆结果
Inv_done	output	1	模逆完成标识

二进制扩展Euclidean算法

输入：模逆使能信号inv_en，整数0<a<p

输出：a^-1mod p

1. u=a,v=p,A=1,C=0;
2. 若 ,重复执行步骤2，否则直接返回C=0

　　　　2.1.  若u为偶数，重复执行2.1节

　　　　　　2.1.1.  u=u/2。

　　　　　　2.1.2. 若A为偶数，则A=A/2，否则A=(A+P)/2。

　　　　2.2.  若v为偶数，重复执行2.2节

　　　　　　2.2.1. v=v/2。

　　　　　　2.2.2. 若C为偶数，则C=C/2；否则C=(C+P)/2。

　　　　2.3. 若 ,则u=u-v,A=A-C;否则v=v-u,C=C-A。

　　  3.返回（C mod p）。

为验证模逆算法正确性，我们选取一个简单的椭圆曲线进行验证，选取的曲线为见以往算法模块，其中a = 4;  p = 29

选用输入inv_in = 15,仿真结果为2，15*2=30 mod 29 = 1（mod29），结果正确。

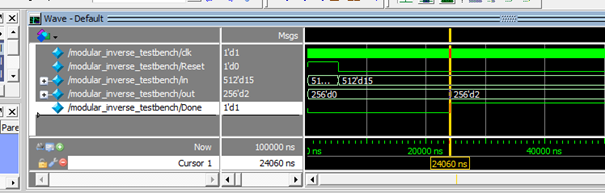
代码如下：

module mod_inv (
    input                clk,
    input                reset,
    input                 mod_inv_en,
    input                 mod_inv_end,
    input        [511:0] in,
    input        [255:0] params_p,
    output        [255:0] out,
    output                mod_inv_done
);

    /*Since Z = 2 for the case of binary polynomials, all divisions can be preformed via a right shift, and all
    **divisibility checks can be preformed by checking the least signifigant bit.
    **Since the only elliptic curve operations we have to worry about are point doubling and point adding, we're
    **not concerned with numbers greater than 2P, which will be limited to 257 bits
    **
    **UPDATE 11/22: Ditched that assumption, now allows inputs up to 512 bits instead of 257
    */

    //parameter params_p = 256'hFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F;

    //Control Signals
    reg             u_load, v_load, g1_load, g2_load, count_load;
    reg        [511:0]    u_in, v_in, g1_in, g2_in;
    reg        [10:0]    count_in;
    reg                mod_inv_done_r;
    reg     [255:0] out_r;
    wire    [511:0] u_out,v_out,g1_out,g2_out;
    wire    [10:0]    count_out;

    //state machine states
    reg    [2:0]    state, next_state;
    parameter    Init        =    3'd0;
    parameter    Start        =    3'd1;
    parameter     Check_u        =    3'd2;
    parameter    Check_v        =    3'd3;
    parameter    Check_deg    =    3'd4;
    parameter    Wait        =    3'd5;
    parameter    Finish        =    3'd6;

    //Register Instatntations
    reg_256 #(512) u(.clk(clk), .load(u_load), .data(u_in), .out(u_out));
    reg_256 #(512) v(.clk(clk), .load(v_load), .data(v_in), .out(v_out));
    reg_256 #(512) g1(.clk(clk), .load(g1_load), .data(g1_in), .out(g1_out));
    reg_256 #(512) g2(.clk(clk), .load(g2_load), .data(g2_in), .out(g2_out));

    reg_256 #(11) counter(.clk(clk), .load(count_load), .data(count_in), .out(count_out));

    //state machine behavior
    always@(posedge clk) begin
        if(reset)
            state <= Init;
        else
            state <= next_state;
    end

    //Next state Logic
    always@(*) begin
        next_state = state;
        case(state)
            Init: if(mod_inv_en && in != 0 )
                        next_state = Start;
                    else if(mod_inv_en && in == 0 )
                        next_state = Finish;
                    else
                        next_state = Init;
            Start: begin
                if(u_out == 512'b01 || v_out == 512'b01)
                    next_state = Wait;
                else if(u_out[0] == 0)
                    next_state = Check_u;
                else if(v_out[0] == 0)
                    next_state = Check_v;
                else
                    next_state = Check_deg;
            end
            Check_u: begin
                if(u_out[0] == 0)
                    next_state = Check_u;
                else if(v_out[0] == 0)
                    next_state = Check_v;
                else
                    next_state = Check_deg;
            end
            Check_v: begin
                if(v_out[0] == 0)
                    next_state = Check_v;
                else
                    next_state = Check_deg;
            end
            Check_deg:
                next_state = Start;
            Wait:
                if(count_out == 11'd470) next_state = Finish;
            Finish:
                next_state =  mod_inv_end ? Init : Finish;
            default:
                next_state = Init;
        endcase
    end

    always@(*) begin
        //Default values
        u_in = u_out;
        v_in = v_out;
        g1_in = g1_out;
        g2_in = g2_out;
        u_load = 1'b0;
        v_load = 1'b0;
        g1_load = 1'b0;
        g2_load = 1'b0;
        out_r = 256'b0;
        mod_inv_done_r = 1'b0;
        count_load = 1'b1;
        count_in = count_out + 1;
    //Preform algorithm steps
        case(state)
            Init: begin
                u_in = in;
                v_in = params_p;
                mod_inv_done_r = 1'b0;
                g1_in = 512'b01;
                g2_in = 512'b0;
                u_load = 1'b1;
                v_load = 1'b1;
                g1_load = 1'b1;
                g2_load = 1'b1;
                count_in = 0;
            end
            Start:begin end
            Check_u: begin
                u_in = u_out>>1;    //Divide by z (z=2)
                if(g1_out[0] == 0)
                    g1_in = g1_out>>1;
                else
                    g1_in = (g1_out + params_p)>>1;
                if(u_out != 512'b01 && u_out[0] == 0) begin
                    u_load = 1'b1;
                    g1_load = 1'b1;
                end
            end
            Check_v: begin
                v_in = v_out>>1;
                if(g2_out[0] == 0)
                    g2_in = g2_out>>1;
                else
                    g2_in = (g2_out + params_p)>>1;
                if(v_out != 512'b01 && v_out[0] == 0) begin
                    v_load = 1'b1;
                    g2_load = 1'b1;
                end
            end
            Check_deg: begin //Checks if deg(u) > deg(v)
                if(u_out > v_out && u_out >= ((v_out<<1) - v_out)) begin
                    u_in = u_out + v_out;
                    g1_in = g1_out + g2_out;
                    u_load = 1'b1;
                    g1_load = 1'b1;
                end
                else begin
                    v_in = v_out + u_out;
                    g2_in = g2_out + g1_out;
                    v_load = 1'b1;
                    g2_load = 1'b1;
                end
            end
            Wait:
                if(count_out != 11'd470)
                    count_in = count_out + 1;
            Finish: begin
                mod_inv_done_r = 1'b1;
                if(in == 0)
                    out_r = 0;
                else if(u_out == 512'b01 && in != 0)
                    out_r = g1_out[255:0];
                else if(u_out != 512'b01 && in != 0)
                    out_r = g2_out[255:0];
                else
                    out_r = g2_out[255:0];
            end
            default: begin end
        endcase
    end
    assign out = (state==Finish)? out_r : 0;
    assign mod_inv_done = (state==Finish)? mod_inv_done_r : 0;
endmodule