浅谈KMP模式匹配算法

普通的模式匹配算法(BF算法)

子串的定位操作通常称为模式匹配算法

假设有一个需求，需要我们从串“a b a b c a b c a c b a b"中，寻找内容为“a b c a c”的子串。

此时，称“a b a b c a b c a c b a b"为主串S，“a b c a c”为模式串T。

很容易想到，通过遍历主串S，与模式串T的首字母逐一比对，当主串S中的某一元素i与模式串T首字符j相同，则将主串S中第i+1个字符与模式串T的j+1个字符继续匹配。若匹配成功，则继续将主串S中的第i+2个字符与模式串T中的第j+2个字符进行比对。若匹配失败，则将主串S的第i+1个字符与模式串的第j个字符重新比对....

将上述文字转化为图像如下：

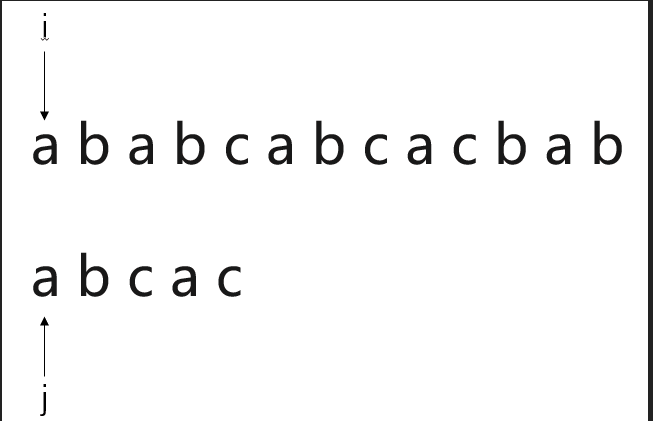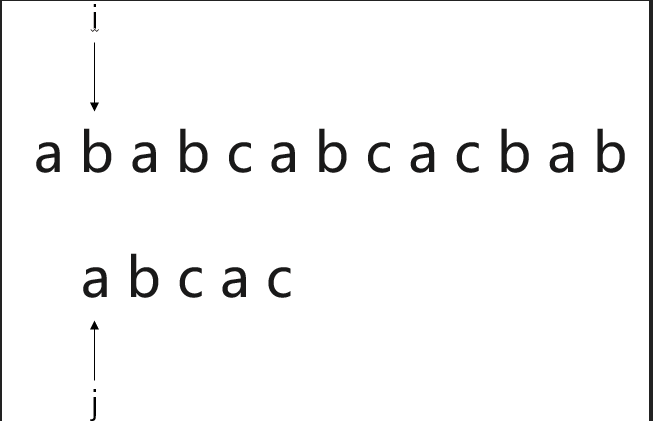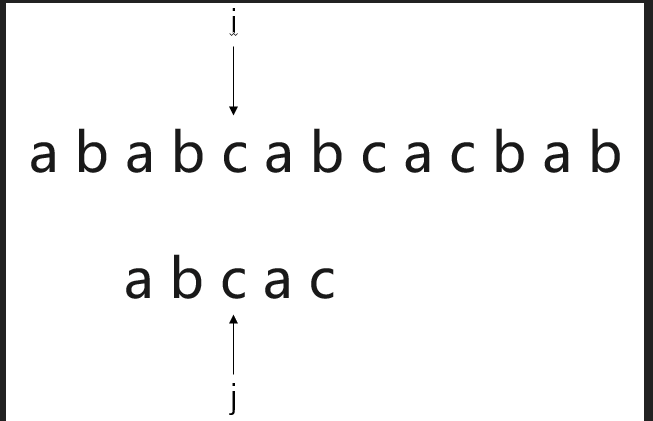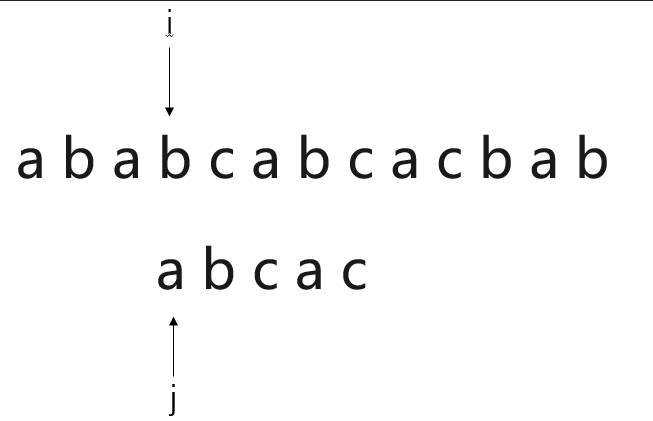
按照动画的显示效果很容易理解BF模式匹配算法。

通过分析可以得出，每次匹配失败之后，i的指向又将回到主串S的i-j+2位置

通过C语言伪代码的方式实现：

若将主串S的长度看作m，将模式串T的长度看作n

则该代码的时间复杂度为O(m+n)

BF算法确实实现了模式匹配的目的，但同时也有较大的缺陷

模式匹配改进算法(KMP算法)的引出

假设目前有这样一个主串S与模式串T

主串S：

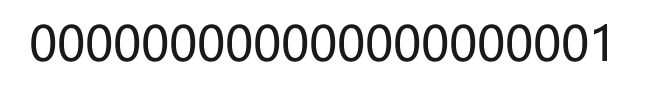
模式串T：

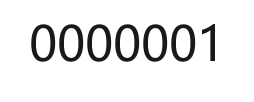
比对过程：

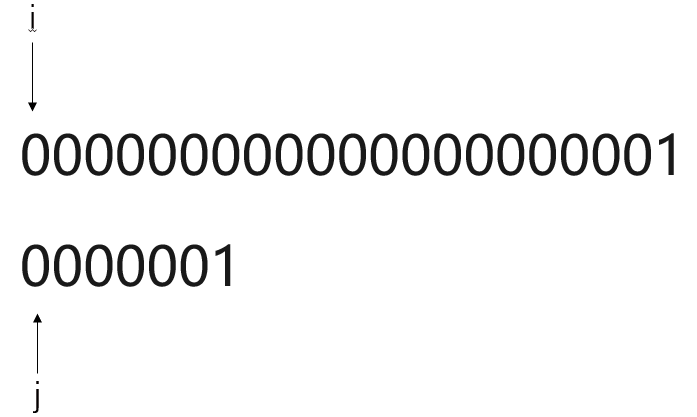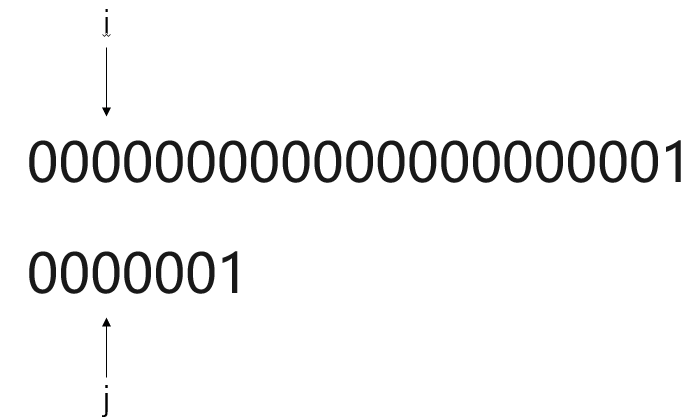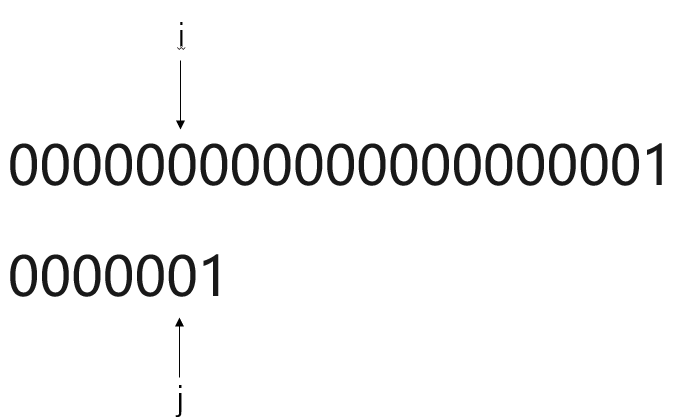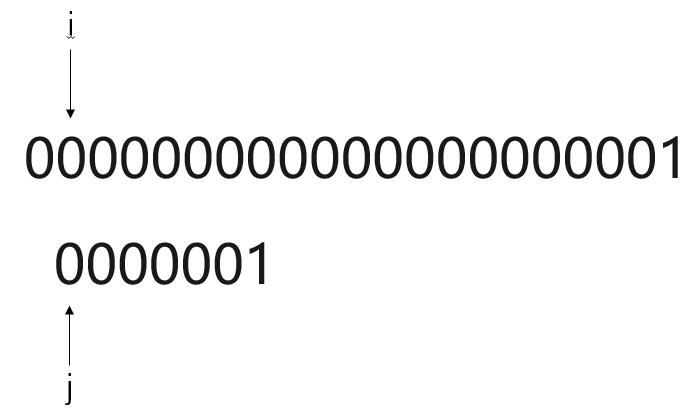
显而易见，使用BF模式匹配算法，一旦遇到主串S元素与模式串T高度重合，但鲜有不同。

此种算法将进行大量重复的“主串S回退”，如此一来，时间复杂度将达到

O(m*n)

而后，D.E.Knuth与V.R.Pratt和J.H.Morris发现了一套模式匹配的改进算法，根据他们的名字的字母，该算法被命名为：

KMP算法

KMP算法

KMP算法基本概念

KMP算法可以在时间复杂度为O(m+n)的时间数量级上完成模式匹配操作。

其不同点在于，在匹配失败之后，不需要回溯i指针

而是利用已经“部分匹配”的结果，将模式串T向右滑动尽可能远的距离

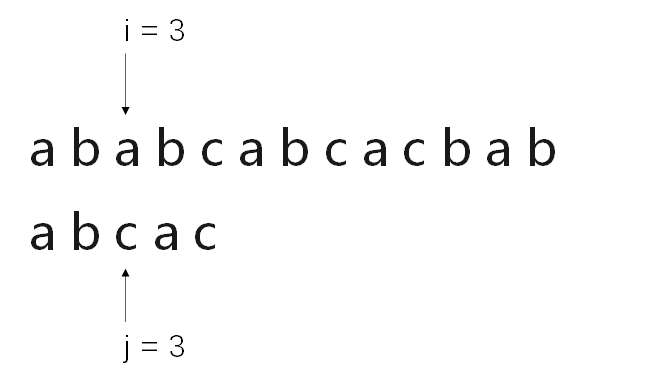
(KMP算法比对过程1)

(KMP算法比对过程2)

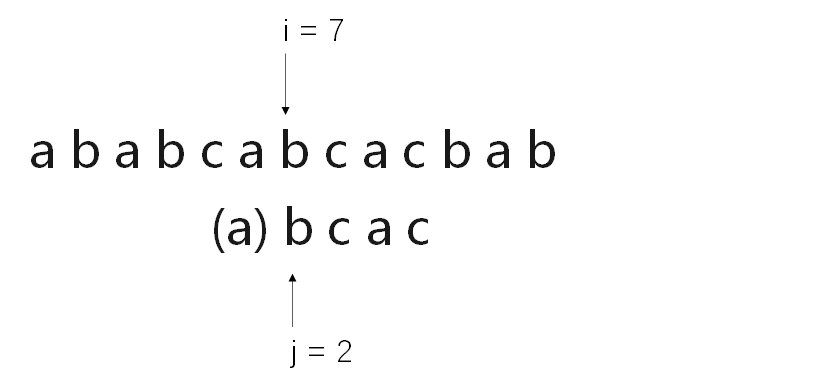
(KMP算法比对过程3)

从该描述中我们提取出要使用KMP算法最核心的三个问题：1.滑动的条件 2.滑动的模式 3.滑动距离k的求解

滑动的条件

这部分我们探究当发生“失配”后，主串S中的i应该与模式串T中的第几个字符(这里用K指代)继续进行比较。

在什么条件下我们可以将窗口进行“滑动”？或者说，怎样才叫发生了“部分匹配”？

这里给出严蔚敏版的《数据结构》中，对于“部分匹配”条件的定义(模式串为p，主串为s)：

①

\[p_1p_2...p_{k-1} = s_{i-k+1}s_{i-k+2}...s_{i-1}
\]

②

\[p_{j-k+1}p_{j-k+2}...p_{j-1} = s_{i-k+1}s_{i-k+2}...s_{i-1}
\]

③

\[p_1p_2...p_{k-1} = p_{j-k+1}p_{j-k+2}...p_{j-1}
\]

刚看到这三个公式的时候，有点懵，但仔细比对之后可以发现

公式①说明：模式串p从头开始的子串与后面某段已发生“部分匹配”的主串s的子串q相同

公式②说明：模式串p在除开头以外，有一段子串与刚才的子串q发生了“部分匹配”

公式③说明：如果满足上述两个条件，则可以得出模式串p中有两端相同的子串

如果满足以上三个条件(满足前两个条件则第三个必定满足),则可以快速“滑动k个位置”来进行KMP模式匹配

滑动的模式

明确了前提条件之后，我们建立应该next[j]来保存每次比对结束后的K值

约定：

next[j]	条件	结果
0	当j等于1	将i向后移动一位
k	取Kmax，1<k<j 且满足条件③	将模式串的第k位与当前i对齐
1	其他情况	将模式串的第1位与当前i对齐

反映成代码形式：

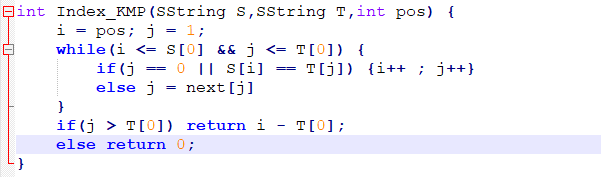
滑动距离K的求解

由

\[p_1p_2...p_{k-1} = p_{j-k+1}p_{j-k+2}...p_{j-1}
\]

可知next[j]仅与模式串有关而与主串无关

这里是整个KMP算法的核心部分，在我反反复复看几十遍严蔚敏版的《数据结构》之后，我终于理清了整个求解滑动距离的方法。

整个算法分为两个情况：

\[p_k = p_j
\]

以及

\[p_k ≠ p_j
\]

若满足第一种情况，有

next[j+1] = next[j] + 1;

若满足第二种情况，则又分为两种情况

设K' = next[k],当P[K'] = P[j] 时，有

next[j+1] = next[k] + 1;
如果一直移动K'到j = 1时，还不能找到对应的P[K'] = P[j],那么直接有

next[j+1] = 1;

在展开讲求next[j]的算法之前，必须要明确的一点是：

k，j，k'，j+1分别代表串中的哪些位置

在这里给出明确定义：

j+1就是你需要求k值的模式串位置
j就是当前需要求出K值的字符的前一个字符
k-1就是“已匹配”的前缀的最后一个字符
k就是“已匹配”的前缀的最后一个字符的后一个字符

注意

前缀一定要包含第1个字符
后缀一定要包含希望求得K的字符的前一个字符

如图所示，如果我们要求得串中第5个字符的K值，假设前四个字符K值均已经求得，设我们的目标字符指针为j+1

又有第1个‘a’与第3个‘a'匹配，所以他们分别为k-1和j-1

因此第2个字符为k，第4个字符为j。

重点来了

让我们抛出一个例子，来理解next[j]的求法

假设我们已知j=1，2，3，4的next[j]值分别为：0，1，1，2

由于k-1和j-1已经”匹配“，则满足前置匹配条件，我们来比较pk和pj的内容，

pk = b，pj = a；

可见它们并不相等，因此k指向的b会甩锅给“next[k]”字符，而next[k] = 1，也就是串的第一个字符‘a'

第一个字符‘a'成功与第j个字符‘a'相匹配，因此依照我们定义的的pk ≠ pj的第一种情况可以得到

next[j+1] = next[k] + 1 = 2;

由此，我们可以通过之前定义的方式来确定所有的next[j]的值，下面给出串'abaabcac'的所有next[j]的值：

希望读者能拿起笔，从next[2]开始，计算到next[8]

相信计算完上表格的读者，已经对next[j]的计算方法有了更加深刻的理解

在这里我也分享出自己总结的口诀：

k，j相等，直接加1
k，j不等，层层甩锅
甩锅失败，直接赋1
甩锅成功，老板加1

释义：

pk = pj：next[j+1] = next[j] + 1;
pk ≠ pj: 甩锅
p[k'] = pj:next[j+1] = next[k] + 1;
p[k'] ≠ pj:next[j+1] = 1 or 继续向next[k']甩锅。

接下来给出代码实现求next[j]：

KMP算法的改进

通过分析代码我们可以发现，当模式串元素有多个重复元素：

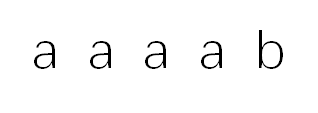
他们的next[j]为：0，1，2，3，4

因此在比对时将出现i不动，j从调用next[j]3次的情况，

在这种情况下，我们可以让j=1，2，3，4只进行一次比对就使得i向后移动一位（也就是next[j] = 0)

改进算法如下：

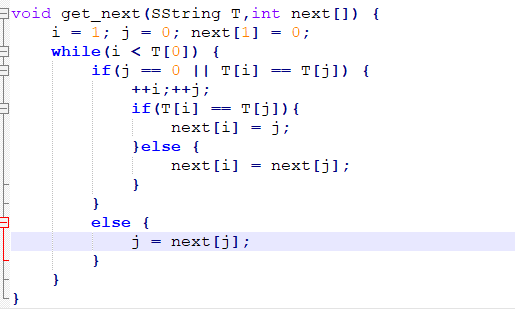
改进之后next[j] = 0,0,0,0,4,成功避免了重复比对