Proximal Algorithms 7 Examples and Applications

目录

• LASSO
  • proximal gradient method
  • ADMM
• 矩阵分解
  • ADMM算法
• 多时期股票交易
• 随机最优
• Robust and risk-averse optimization
  • method

本节介绍一些例子.

LASSO

考虑如下问题:

\[\min \quad (1/2)\|Ax-b\|_2^2 + \gamma\|x\|_1,
\]

其中\(x \in \mathbb{R}^n, A \in \mathbb{R}^{m\times n }\).

proximal gradient method

proximal gradient method 是：

\[x^{k+1} := \mathbf{prox}_{\lambda g}(x^k - \lambda \nabla f(x^k))
\]

令\(f(x)=(1/2)\|Ax-b\|_2^2, g(x)=\gamma \|x\|_1\), 则

\[\nabla f(x) = A^T(Ax-b), \quad \mathbf{prox}_{\gamma g}(x)=S_{\gamma}(x),
\]

其中\(S_{\gamma}(x)\)是soft-thresholding.

ADMM

很自然的方法，不提了.

矩阵分解

一般的矩阵分解问题如下:



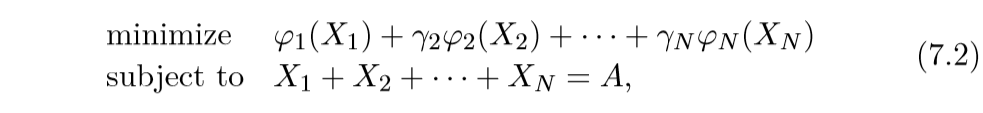
其中\(X_1, \ldots, X_N \in \mathbb{R}^{m\times n}\)为变量，而\(A \in \mathbb{R}^{m\times n }\)为数据矩阵.

不同的惩罚项\(\varphi\)会带来不同的效果.

• \(\varphi(X)=\|X\|_F^2\), 这时，矩阵元素往往都比较接近且小
• \(\varphi(X)=\|X\|_1\), 这会导致稀疏化
• \(\varphi(X) = \sum_j \|x_j\|_2\), 其中\(x_j\)是\(X\)的第\(j\)列, 这会导致列稀疏?

其他的看文章吧.

ADMM算法

令

\[f(x) = \sum_{i=1}^N \varphi_i (X_i), \quad g(X)=I_{\mathcal{C}}(X),
\]

其中\(X = (X_1, \ldots, X_N)\), 并且：

\[\mathcal{C} = \{(X_1, \ldots, X_N| X_1 + \ldots + X_N=A\}.
\]

根据之前的分析，容易知道:

\[\Pi_{\mathcal{C}}=(X_1, \ldots, X_N)-\bar{X}+(1/N)A,
\]

其中\(\bar{X}\)是\(X_1, \ldots, X_N\)的各元素的平均.

最后算法总结为：

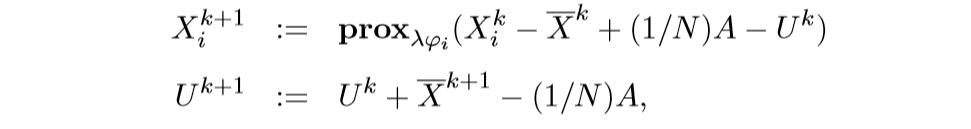
多时期股票交易

其问题是:

\[\min \quad \sum_{t=1}^T f_t(x_t) + \sum_{t=1}^T g_t (x_t - x_{t-1}),
\]

其中\(x_t, t=1,\ldots, T\)表示第\(t\)个时期所保持的股份，期权，而\(f_t\)则表示对应的风险，\(g_t\)表示第\(t\)个时期交易所需要耗费的资源.

考虑如下分割:

\[f(X)=\sum_{t=1}^ Tf_t(x_t), \quad g(X)=\sum_{t=1}^T g_t(x_t-x_{t-1}),
\]

其中\(X=[x_1, \ldots, x_T]\in\mathbb{R}^{n \times T}\).

随机最优

为如下问题:

\[\min \quad \sum_{k=1}^K \pi_k f^{(k)} (x),
\]

其中\(\pi \in \mathbb{R}_+^K\)是一个概率分布，满足\(1^T\pi=1\).

利用第5节的知识，将此问题化为:

\[\min \quad \sum_{k=1}^K \pi_k f^{(k)} (x^{(k)}) \\
s.t. \quad x^{(1)}=\ldots=x^{(K)}.
\]

再利用ADMM就可以了.

Robust and risk-averse optimization

鲁棒最优，特别的, 最小化最大风险:

\[\min \quad \max_{k=1, \ldots, K} f^{(k)}(x).
\]

更一般的:

\[\min \quad \varphi(f^{(1)}, \ldots, f^{(K)}(x)),
\]

其中\(\varphi\)为非降凸函数.

method

将上面的问题转化为:

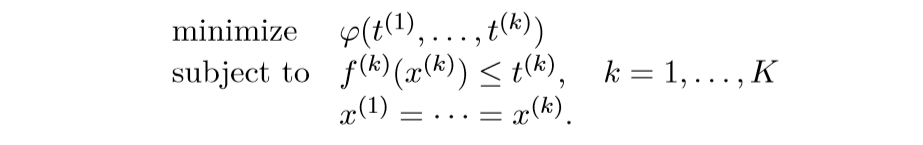
将



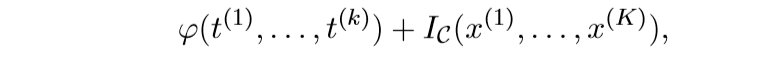
视作\(f\)

而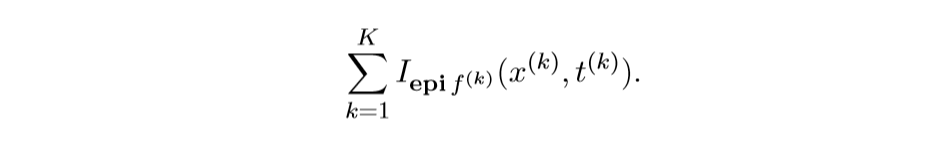

作为\(g\)，再利用ADMM求解即可.