封面是福州的福道，从高处往下看福道上的人在转圈圈。从傅里叶变换后的频域角度来看，我们的生活也是一直在转圈圈，转圈圈也是好事，说明生活有规律，而我们应该思考的是，如何更有效率地转圈圈……哦别误会，我真不是在说内卷（狗头）。

本文会讲到离散傅里叶、实信号、负频率、fftshift、实信号、共轭等概念。

离散傅里叶变换

上一篇文章里面写到了离散傅里叶变换。

公式如上，我发现，只要掌握初中的数学——加减乘除以及三角函数，就可以掌握离散傅里叶变换的运算。

上文中说过：

如果有时域数据如: [1, 2, 3] 的话，

那么代入公式算得频域数据的结果为:

[6 + 0i, -1.5 + 0.86603i, -1.5 - 0.86603i]

频域数据，就是时域数据依次代入到离散傅里叶变换公式的结果。

下面是对频域数据第二个复数：-1.5 + 0.86603i的推算过程。如下：

此时N = 3，k = 1，n = [0, 1, 2]代入到上述公式得：

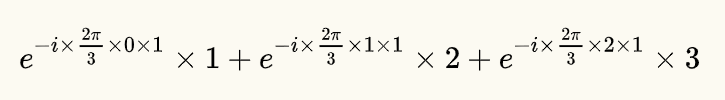
只要懂得计算:

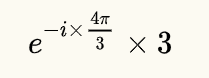
即可得出整个式子的结果。以上式子表达的即为，一个长度为3的线段，一端在坐标原点上，且线段和X轴（实部）的正半轴重叠。然后线段以坐标原点为圆心，顺时针旋转4π/3。该线段在X轴上的投影即为实部，在Y轴上的投影即为虚部。如下(手残字丑预警)：

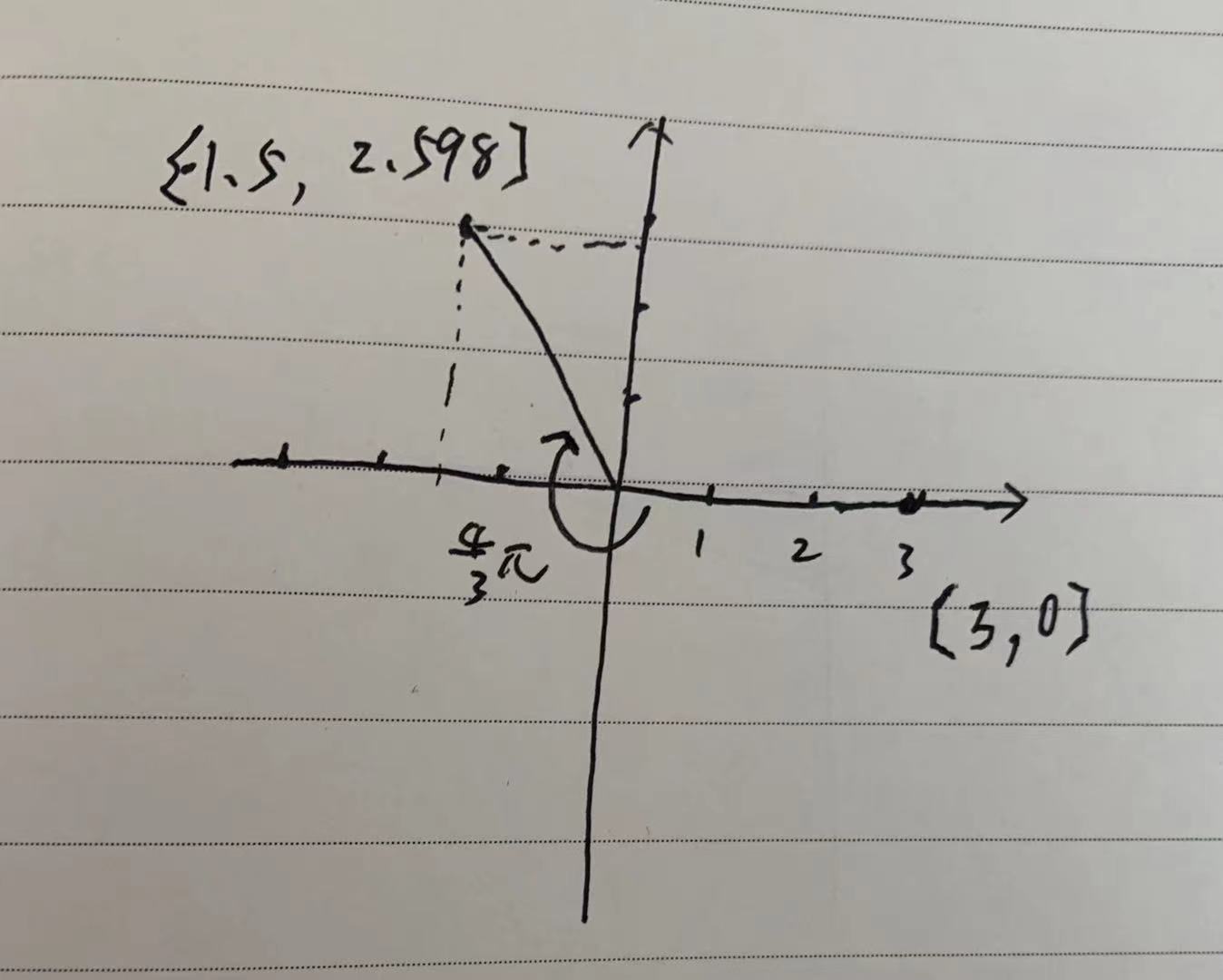
这里多说一句，如果时域信号也是复数且虚部有值的话，例如[3, 1]，那么上图中，起始位置的[3, 0]改成[3, 1]即可，再做同样的4π/3旋转。

实部：-3 * cos(π/3) = -1.5

虚部：3 * sin(π/3) = 2.59808

即为:

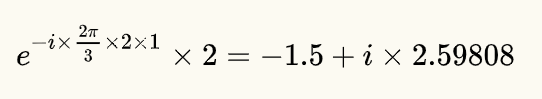
同理可得：

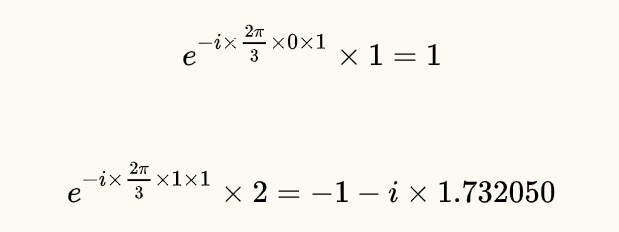
以上相加：

1 + (-1 - i*1.732050) + (-1.5 + i*2.59808) = -1.5 + 0.86603i

至此，我们大约已经掌握了DFT（离散傅里叶变换）。DFT即计算三角函数和数据累加的过程，甚至我们也可以自己实现一个DFT函数。

fftshift

FFT即快速傅里叶变换，一种非常高效的DFT函数实现。

通常做完FFT之后，很多场景下会做fftshift。

fftshift是针对频域的，将FFT直流分量移到频谱中心。fftshift就是对换数据的左右两边置换如：

x=[1 2 3 4]

fftshift(x) -> [3 4 1 2]

用matlab或者octave运行以下代码：

clf;

fs=100;N=256;  %采样频率和数据点数

n=0:N-1;t=n/fs;   %时间序列

x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号

y1=fft(x,N);   %对信号进行快速Fourier变换

y2=fftshift(y1);

mag1=abs(y1);    %求得Fourier变换后的振幅

mag2=abs(y2);    

f1=n*fs/N;   %频率序列

f2=n*fs/N-fs/2;

subplot(2,1,1),plot(f1,mag1,'r');  %绘出随频率变化的振幅

xlabel('Freq Hz');

ylabel('Amp');title('plot 1 usual FFT','color','r');grid on;

subplot(2,1,2),plot(f2,mag2,'m');  %绘出随频率变化的振幅

xlabel('Freq Hz');

ylabel('Amp');title('plot 2 FFT after fftshift','color','m');grid on;

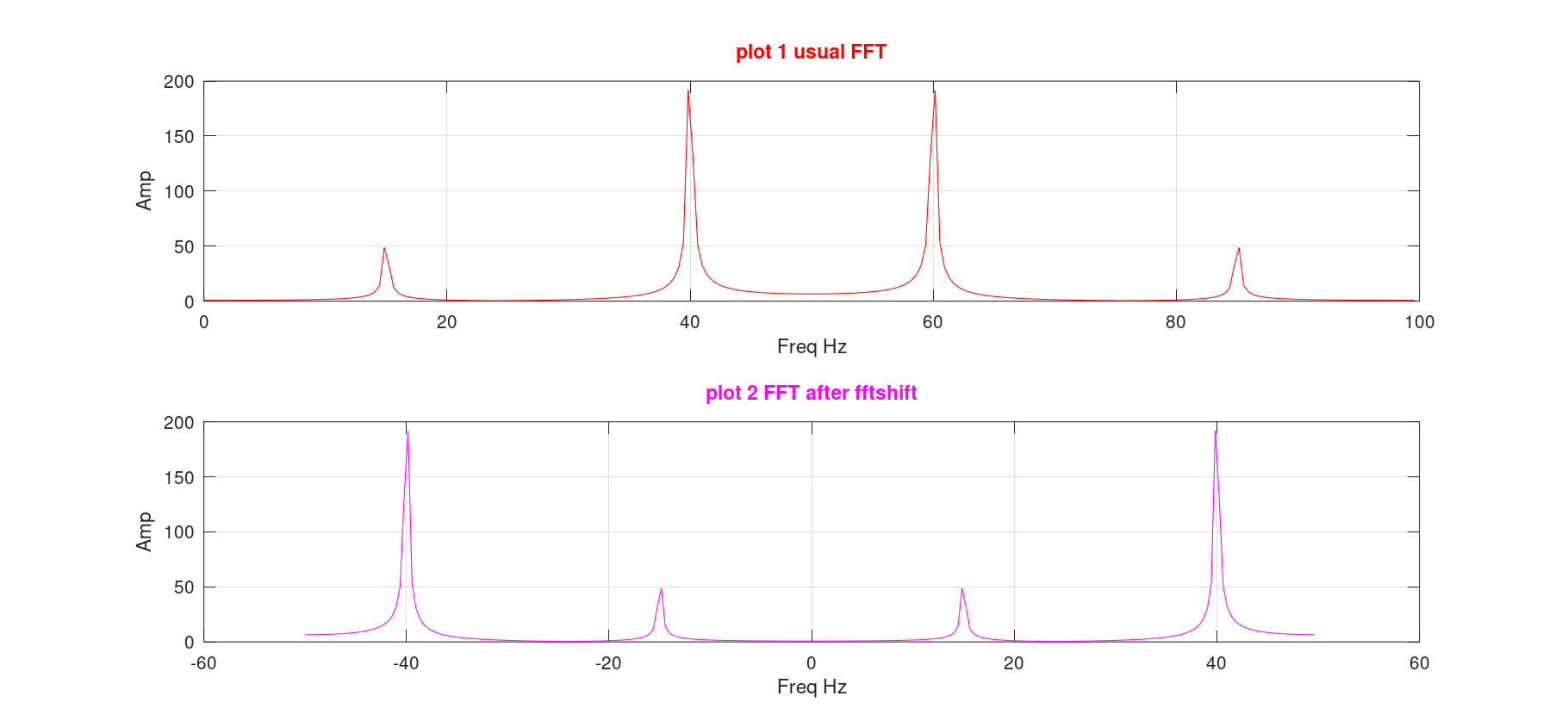
可以看到fftshift完成了shift的功能，但也暗含了额外的信息。

为什么60Hz可以当做是-40Hz，15Hz可以当做是-85Hz？又或者为什么会有负频率？
为什么频点40和-40有相同的振幅？

接下来就这两点展开讨论。

负频率

我们还是以时域数据[1, 2, 3] fft后 --> [6 + 0i, -1.5 + 0.86603i, -1.5 - 0.86603i]，作为例子。

[6 + 0i, -1.5 + 0.86603i, -1.5 - 0.86603i] 中的三个数字分别代表0Hz, 1Hz, 2Hz的频点信息。对它做fftshift则会变成：

[-1.5 - 0.86603i, 6 + 0i, -1.5 + 0.86603i]这分别代表-1Hz，0Hz，1Hz的频点信息。原本的2Hz的也就是-1Hz。

为什么？还是要从离散傅里叶变换的公式说起：

还记得我们求频域数据[6 + 0i, -1.5 + 0.86603i, -1.5 - 0.86603i] 中1Hz的-1.5 + 0.86603i的式子吗？

如果求2Hz的式子是这样的：

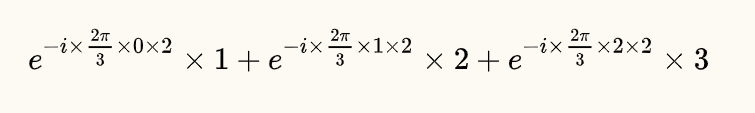
即为：

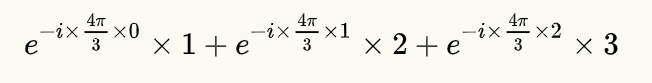
也即为:

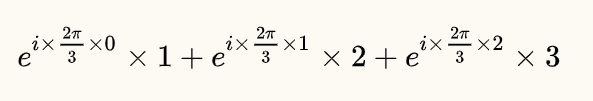
以上求2Hz的式子和以下求1Hz的式子再对比一下：

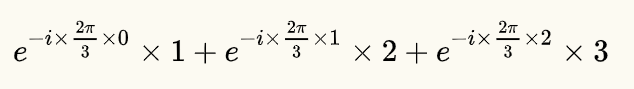
1Hz是顺时针旋转，2Hz是逆时针旋转，旋转的度数是一样的，只是旋转的方向不一样。

所以当N为3时，2Hz即为-1Hz，就是相对1Hz反着旋转。

以上现象公式是可以推导出来的，如下：

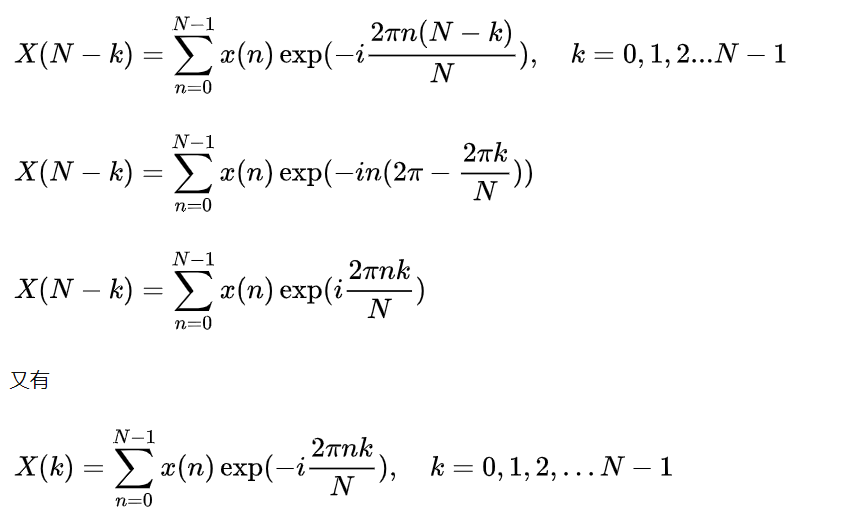
实信号的频域，共轭对称

为什么频点40和-40有相同的振幅？因为时域信号是实信号，所谓实信号，即为信号中数据的虚部为0。

所谓共轭，就是实部相同，虚部的符号相反的一对复数。

实信号经过DFT之后，频域信号是共轭对称的，两个数如果共轭，则代表这两个值的幅值相同，相位不同。频点40和-40频点的值是共轭的，所以有相同的振幅。

我们还是以[1, 2, 3]为例子，实信号[1, 2, 3]的频谱是[6 + 0i, -1.5 + 0.86603i, -1.5 - 0.86603i]。

1Hz的-1.5 + 0.86603i和-1Hz的-1.5 - 0.86603i就是共轭对称的。这不是巧合。

这也是暗含在离散傅里叶变换公式中的一个信息。可以推导出来，这还是牵扯到1Hz和-1Hz的频点信息的关系，如下：

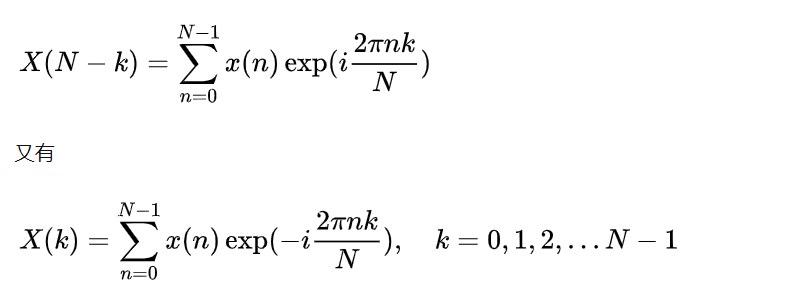
如果x(n)是实信号，那么X(k)与X(N - k)则互为共轭，怎么理解？

其中 $$ e^{-i\times \frac{2\pi nk}{N}} $$ 和 $$ e^{i\times \frac{2\pi nk}{N}} $$ 已经是互为共轭了，就看x(n)的值中的虚部是否为零了。

示意图如下(手残字丑预警)：

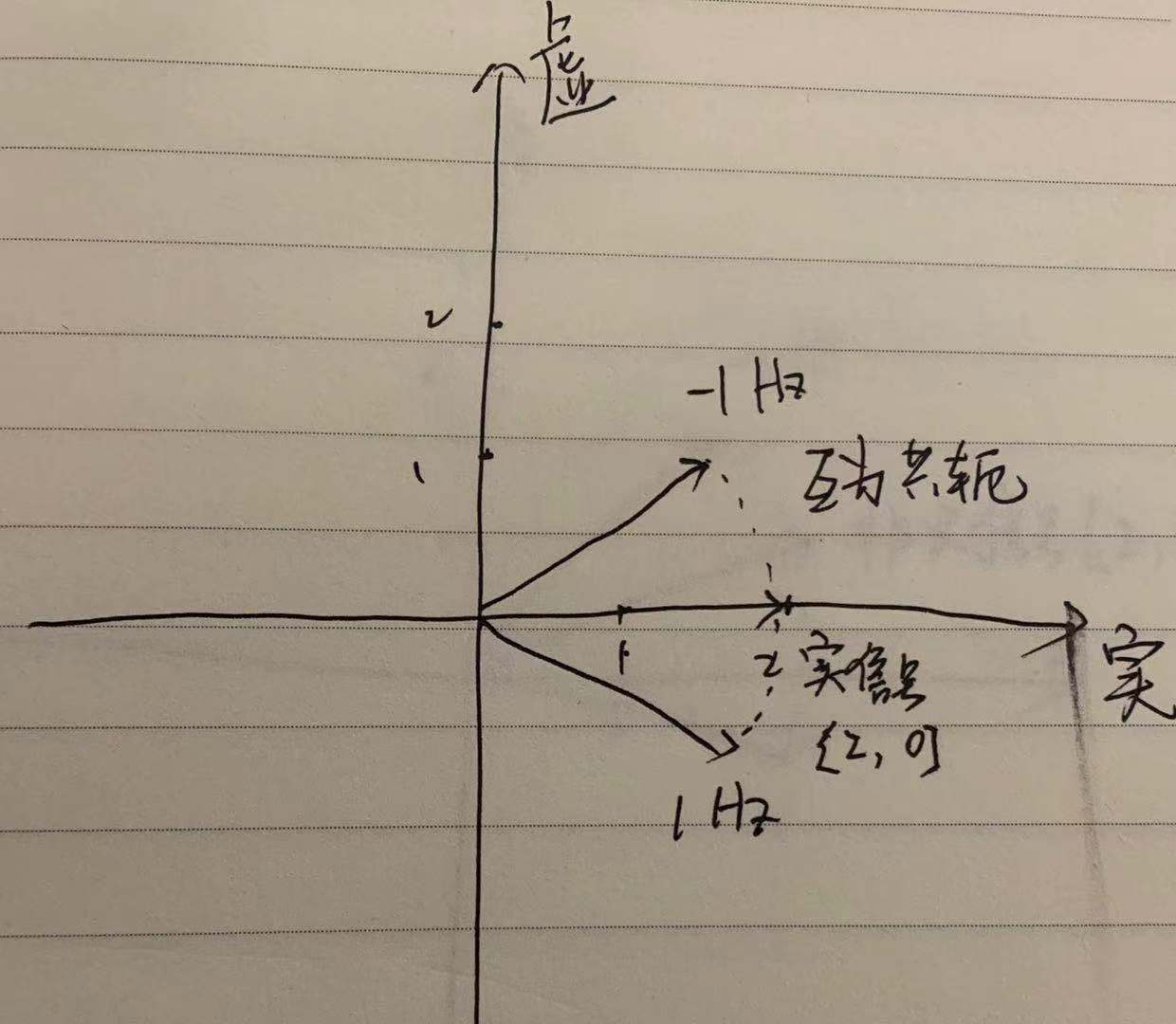
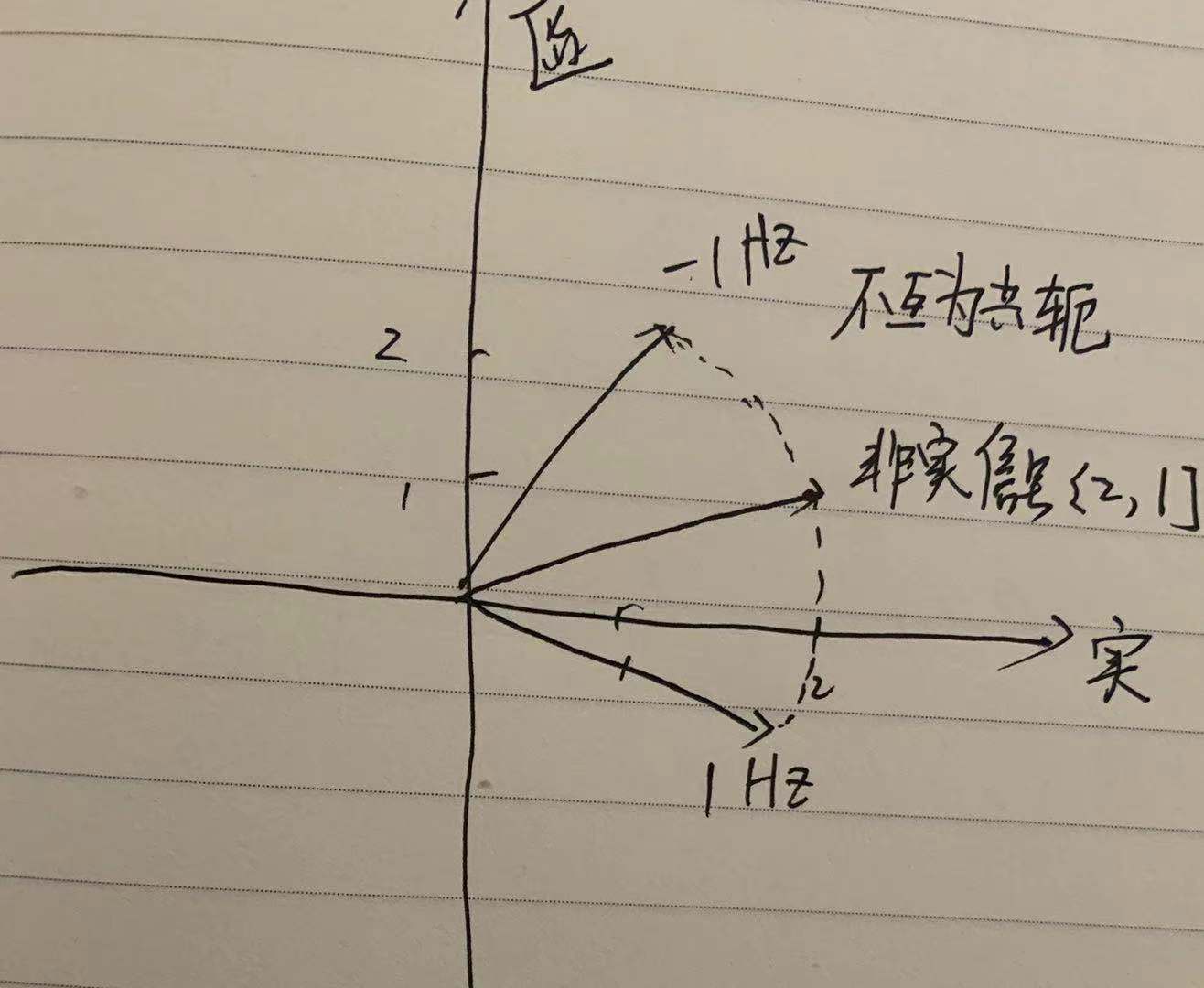
以上简化了生成1Hz的多个向量，仅为示意，但是1Hz和-1Hz频点的关系一目了然，也解释了为什么仅在实信号时，正负频率是共轭的。

思考另一个角度

频域信号中所有频点代表的曲线，他们的累加即为时域信号。

想象一下（其实是我不会画图 - -），在一个复平面上如何构建一个，在实部投影是40Hz的cos信号，但虚部投影是0的曲线？

我们是否需要两个复平面曲线，一个如下图，假设它的相位和幅值是a + bi，并且以40Hz的频率逆时针旋转。

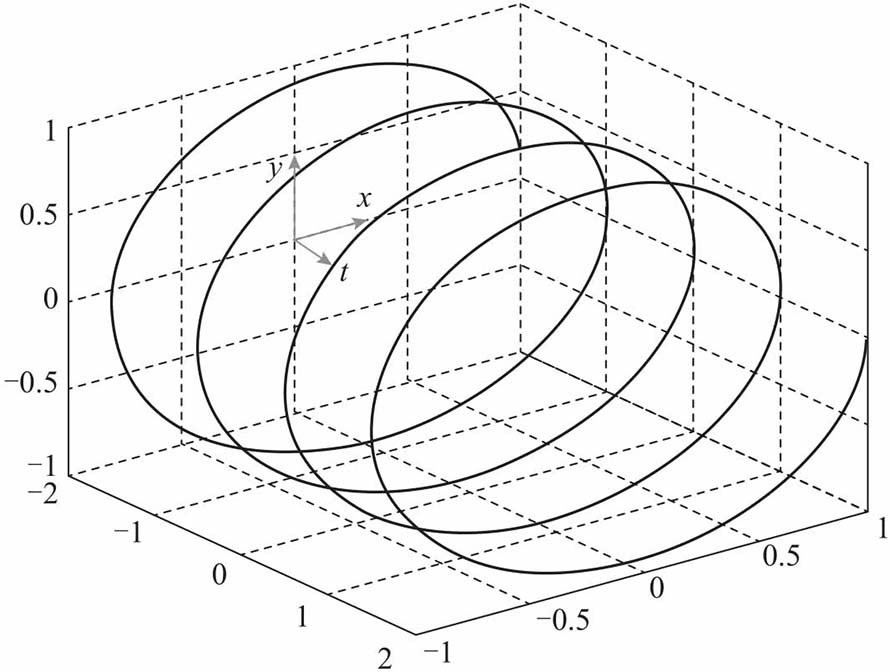
另一个自行脑补，假设它的相位和幅值是a - bi，并且以40Hz的频率顺时针旋转。

以上两个曲线相加，是否能在一个复平面上如何构建一个，在实部投影是40Hz的cos，但虚部投影是0的曲线呢？

如果本文中有哪些没说清楚的地方，欢迎后台私信我，一起讨论。

参考资料