[codeforces113D]Museum

D. Museum

time limit per test:

2 seconds

memory limit per test:

256 megabytes

input:

standard input

output:

standard output

One day as Petya and his friend Vasya were having one of their numerous trips, they decided to visit a museum castle. The museum has a specific shape: it consists of n rooms connected with m corridors so that one can access any room from any other one.

After the two friends had a little walk around the museum, they decided to split and watch the pieces of art each of them found interesting. They agreed to meet in one of the rooms at six p.m. However, they forgot one quite essential thing: they didn't specify the place to meet and when the time came, they started to rush about the museum looking for each other (they couldn't call each other as roaming made a call's cost skyrocket).

Yet, even despite the whole rush, they couldn't get enough of the pieces of art, that's why each of them has the following strategy: each minute he make a decision where to go — with probability pi he doesn't move to any other place during this minute (i.e. he stays in the room). With probability 1 - pi he equiprobably choose one of the adjacent rooms and went there along the corridor. Here i is the ordinal number of the current room. Building was expensive in ancient times, that's why each corridor connected two different rooms, and any two rooms had no more than one corridor between them.

The boys act simultaneously. As the corridors are dark, it is impossible to meet there; however, one can walk along the corridors in both directions (besides, the two boys can be going through the same corridor simultaneously without meeting). The boys act like that until they meet each other. More formally, the two friends meet when at some moment of time both of them decided to appear in the same room.

For each room find the probability that the boys will meet there considering that at 6 p.m. they are positioned in rooms a and bcorrespondingly.

Input

The first line contains four integers: n (1 ≤ n ≤ 22), representing the numbers of rooms; m 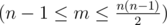, representing the number of corridors; a, b (1 ≤ a, b ≤ n), representing the numbers of Petya's and Vasya's starting rooms correspondingly.

Next m lines contain pairs of numbers — the numbers of rooms connected by a corridor. Next n lines contain probabilities pi(0.01 ≤ pi ≤ 0.99) with the accuracy of up to four digits after the decimal point — the probability to stay in room i.

It is guaranteed that every room can be reached from every other room by corridors.

Output

In the only line print n space-separated numbers, the i-th number should represent the probability that the friends meet in the i-th room with absolute or relative error of no more than 10 - 6.

Examples

input

2 1 1 2
1 2
0.5
0.5

output

0.5000000000 0.5000000000 

input

4 4 1 2
1 2
2 3
3 4
4 1
0.5
0.5
0.5
0.5

output

0.3333333333 0.3333333333 0.1666666667 0.1666666667 

Note

In the first sample the museum is symmetric. That means the probabilities to meet in rooms 1 and 2 are equal. And their sum equals to one. So, each probability equals 0.5.

题解

第一次来cf做题,98个测试点真的是吓到我了

这个题和"hnoi2013游走"比较像,都是无向图瞎跑处理问题

但不一样的是,这个题没有固定的终点

又观察到n比较小,所以我们不妨枚举终点,即对每个点t来说,枚举t,计算t为终点时两个人在t点会面的概率

设在i点停留的概率为p[i],i点出度为du[i]设从i点走向某一点的概率为k[i],则k[i]=(1-p[i])/du[i]

设这两个人一个人在i,一个人在j,则有如下情况:

1°:i==t&&j==t,则f[i][j]=1;

2°:i==j&&i!=t,则f[i][j]=0;

如果均不满足,则

3°f[i][j]=p[i]*p[i]*f[i][j]+k[i]*p[j]*∑{f[u][j],i有边连向u}+p[i]*k[j]*∑{f[i][v],j有边连向v}+k[i]*k[j]*∑{f[u][v],i有边连向u,j有边连向v}

好长一大串啊注意,f[u][j],f[i][v]和f[u][v]可能满足上述条件1°和2°,要特判并处理

这样本题就变成了一个熟悉的问题:解方程组,也就是说高斯消元怎么又是高斯消元啊啊啊

我们的未知量,就是这里的f[i][j]

但是f数组没有一个固定的顺序,所以我们先给每一个数对{i,j(i!=j)}编号,设共有cnt对

设点对{S,T}的编号是num,则对于每个点t来说,答案就是对应编号方程的解了(ans[t]=A[num][cnt+1])

最后,注意特判,即两人一开始就在一间屋子时,除了那个屋子的答案是1,其他屋子都是0,输出就好.

代码见下:

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 const int N=;
 const int M=(N-)*N>>;
 int n,m,S,T,du[N],adj[N],e;
 double A[M][M],p[N],k[N],ans[N];
 struct node{int qi,zhong,next;}s[M<<];
 inline void add(int qi,int zhong)
 {s[++e].zhong=zhong;s[e].qi=qi;s[e].next=adj[qi];adj[qi]=e;}
 int num[N][N],cnt,f[N];
 inline void gasse()
 {
     for(int i=;i<=cnt;i++)
     {
         int p=i;
         for(int j=i+;j<=cnt;j++)
             if(fabs(A[p][i])<fabs(A[j][i]))p=j;
         if(p!=i)
         for(int j=;j<=cnt+;j++)
             swap(A[i][j],A[p][j]);
         for(int j=i+;j<=cnt;j++)
         {
             double tmp=A[j][i]/A[i][i];
             for(int k=i;k<=cnt+;k++)
                 A[j][k]-=tmp*A[i][k];
         }
     }
     for(int i=cnt;i>=;i--)
     {
         for(int j=i+;j<=cnt;j++)
             A[i][cnt+]-=A[j][cnt+]*A[i][j];
         A[i][cnt+]/=A[i][i];
     }
 }
 int main()
 {
     scanf("%d%d%d%d",&n,&m,&S,&T);
     for(int i=;i<=m;i++)
     {
         int a,b;scanf("%d%d",&a,&b);
         add(a,b),add(b,a),du[a]++,du[b]++;
     }
     for(int i=;i<=n;i++)
         scanf("%lf",&p[i]),k[i]=(1.0-p[i])/du[i];
     if(S==T)
     {
         for(int i=;i<=n;i++)
             printf("%.10lf%c",i==S?1.0:0.0,i==n?'\n':' ');
         return ;
     }
     for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
             if(i!=j)
                 num[i][j]=++cnt;
     for(int t=;t<=n;t++)
     {
         memset(f,,sizeof(f));f[t]=;
         for(int i=;i<M;i++)
             for(int j=;j<M;j++)
                 A[i][j]=;
         for(int i=;i<=n;i++)
             for(int j=;j<=n;j++)
             {
                 if(i==j)continue;
                 int nu=num[i][j];
                 A[nu][nu]=1.0-p[i]*p[j];
                 for(int a=adj[i];a;a=s[a].next)
                 {
                     int u=s[a].zhong;
                     int nui=num[u][j];
                     if(u==j)A[nu][cnt+]+=k[i]*p[j]*f[j];
                     else A[nu][nui]-=k[i]*p[j];
                 }
                 for(int b=adj[j];b;b=s[b].next)
                 {
                     int v=s[b].zhong;
                     int nui=num[i][v];
                     if(i==v)A[nu][cnt+]+=p[i]*k[j]*f[i];
                     else A[nu][nui]-=p[i]*k[j];
                 }
                 for(int a=adj[i];a;a=s[a].next)
                     for(int b=adj[j];b;b=s[b].next)
                     {
                         int u=s[a].zhong,v=s[b].zhong;
                         int nui=num[u][v];
                         if(u==v)A[nu][cnt+]+=k[i]*k[j]*f[u];
                         else A[nu][nui]-=k[i]*k[j];
                     }
             }
         gasse();
         ans[t]=A[num[S][T]][cnt+];
     }
     printf("%.10lf",ans[]);
     for(int i=;i<=n;i++)
         printf(" %.10lf",ans[i]);
 } 

codeforces113D