切糕[HNOI2013]

经过千辛万苦小A 得到了一块切糕，切糕的形状是长方体，小A 打算拦腰将切糕切成两半分给小B。出于美观考虑，小A 希望切面能尽量光滑且和谐。于是她找到你，希望你能帮她找出最好的切割方案。

出于简便考虑，我们将切糕视作一个长P、宽Q、高R 的长方体点阵。我们将位于第z层中第x 行、第y 列上(1≤x≤P, 1≤y≤Q, 1≤z≤R)的点称为(x,y,z)，它有一个非负的不和谐值v(x,y,z)。一个合法的切面满足以下两个条件：

1. 与每个纵轴(一共有P*Q 个纵轴)有且仅有一个交点。即切面是一个函数f(x,y)，对于所有1≤x≤P, 1≤y≤Q,我们需指定一个切割点f(x,y),且1≤f(x,y)≤R。

2. 切面需要满足一定的光滑性要求，即相邻纵轴上的切割点不能相距太远。对于所有的1≤x,x’≤P 和1≤y,y’ ≤Q，若|x-x’|+|y-y’|=1，则|f(x,y)-f(x’,y’)| ≤D，其中D 是给定的一个非负整数。

可能有许多切面f 满足上面的条件，小A 希望找出总的切割点上的不和谐值最小的那个，即v(x, y, z)之和最小。

【输入格式】（input.txt）

从文件input.txt中读入数据，输入文件第一行是三个正整数P,Q,R，表示切糕的长P、宽Q、高R。第二行有一个非负整数D，表示光滑性要求。接下来是R个P行Q列的矩阵，第z个矩阵的第x行第y列是v(x,y,z) (1≤x≤P,1≤y≤Q, 1≤z≤R)。

100%的数据满足P,Q,R≤40，0≤D≤R，且给出的所有的不和谐值不超过1000。

【输出格式】（output.txt）

输出文件output.txt 仅包含一个整数，表示在合法基础上最小的总不和谐值。

【输入输出样例】

input.txt                   output.txt

2 2 2                         6

1

6 1

6 1

2 6

2 6

input.txt                    output.txt

2 2 2                            12

0

5 1

5 1

2 5

2 5

【样例解释】

第一组样例中最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1。

第二组样例中最佳切面的f为f(1,1)=f(2,1)=f(1,2)=f(2,2)=1。

【时空限制】

 5s,512MB

【题解】

        看起来好像是个几何问题，其实可以用网络流最小割的思路来解决。贴lyc学长ppt：

将点权转化为边权。由S向(x,y,1)连边，边权为v(x,y,1)。由(x,y,z)向(x,y,z+1)连边，边权为v(x,y,z+1)。最后由(x,y,R)向T连边，边权为INF。此题关键在选择的距离限制，解决方法是由每个点向它相邻的点的下方的第d个点连边，也就是(x,y,z)向(x,y,z-d)连边，边权为INF。

学长的证明：

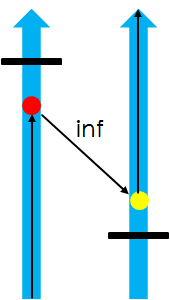
首先假设每条纵轴只割一条边。若两边距离大于d，一定会有图中所示路径，此时需再割一条边。

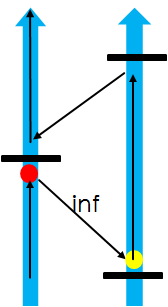
假设再割一条右侧的边，此边与左边割掉的那条边距离要<=d，否则还会出现这样的路径。

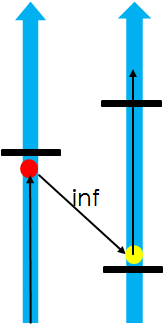
只有距离<=d，才能截断。但此时，右边第一次截断的边已经没有必要了。因为只要上面两条边就可以截断了。因此，每个纵轴只截断一条边，且相邻截断的边距离一定<=d。

除此之外只要注意一下四个方向都要连边，连边时注意边界就好了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int sj=;
int e,s,t,p,q,r,d,cnt,jg;
int h[sj],vl[][][],bm[][][],dep[sj];
struct B
{
     int ne,v,w;
}b[sj*];
queue<int> qi;
void add(int x,int y,int z)
{
     b[e].v=y;
     b[e].w=z;
     b[e].ne=h[x];
     h[x]=e++;
}
void init()
{
     scanf("%d%d%d%d",&p,&q,&r,&d);
     s=;
     t=r*p*q+;
     memset(h,-,sizeof(h));
     for(int i=;i<=r;i++)
       for(int j=;j<=p;j++)
         for(int k=;k<=q;k++)
         {
           scanf("%d",&vl[j][k][i]);
           bm[j][k][i]=++cnt;
         }
     for(int i=;i<=p;i++)
       for(int j=;j<=q;j++)
       {
         add(s,bm[i][j][],vl[i][j][]);
         add(bm[i][j][],s,);
         add(bm[i][j][r],t,0x3fff);
         add(t,bm[i][j][r],);
         for(int k=;k<=r;k++)
         {
           if(k!=r)
           {
              add(bm[i][j][k],bm[i][j][k+],vl[i][j][k+]);
              add(bm[i][j][k+],bm[i][j][k],);
           }
           if(k>d)
           {
              if(i->)
              {
                add(bm[i][j][k],bm[i-][j][k-d],0x3fff);
                add(bm[i-][j][k-d],bm[i][j][k],);
              }
              if(j->)
              {
                add(bm[i][j][k],bm[i][j-][k-d],0x3fff);
                add(bm[i][j-][k-d],bm[i][j][k],);
              }
              if(i+<=p)
              {
                add(bm[i][j][k],bm[i+][j][k-d],0x3fff);
                add(bm[i+][j][k-d],bm[i][j][k],);
              }
              if(j+<=q)
              {
                add(bm[i][j][k],bm[i][j+][k-d],0x3fff);
                add(bm[i][j+][k-d],bm[i][j][k],);
              }
           }
         }
       }
}
bool bfs(int x)
{
     while(!qi.empty()) qi.pop();
     memset(dep,,sizeof(dep));
     dep[x]=;
     qi.push(x);
     while(!qi.empty())
     {
        x=qi.front();
        qi.pop();
        for(int i=h[x];i!=-;i=b[i].ne)
          if(b[i].w&&!dep[b[i].v])
          {
            dep[b[i].v]=dep[x]+;
            if(b[i].v==t) return ;
            qi.push(b[i].v);
          }
     }
     return ;
}
int bj(int x,int y)
{
    return x<y?x:y;
}
int dfs(int x,int f)
{
     if(x==t) return f;
     int ans=,d;
     for(int i=h[x];i!=-;i=b[i].ne)
       if(b[i].w&&dep[b[i].v]>dep[x])
       {
          d=dfs(b[i].v,bj(b[i].w,f));
          f-=d;
          ans+=d;
          b[i].w-=d;
          b[i^].w+=d;
          if(!f) break;
       }
     if(!ans) dep[x]=-;
     return ans;
}
int main()
{
    init();
    while(bfs(s)) jg+=dfs(s,0x7fffffff);
    printf("%d",jg);
    return ;
}

nutcake

我想吃切糕->食堂不卖->粽子都没有->我不开心