DFS和BFS(无向图)Java实现

package practice;

import java.util.Iterator;
import java.util.Stack;

import edu.princeton.cs.algs4.*;

public class TestMain {
    public static void main(String[] args) {
        Graph a = new Graph(6);
        a.addEdge(2, 4);
        a.addEdge(2, 3);
        a.addEdge(1, 2);
        a.addEdge(0, 5);
        a.addEdge(0, 1);
        a.addEdge(0, 2);
        a.addEdge(3, 4);
        a.addEdge(3, 5);
        System.out.println(a);

        DisposeMap df = new DisposeMap(a);
        /*df.dfs(0);
        System.out.println(df.hasPathTo(1));
        System.out.println(df.hasPathTo(2));
        Stack<Integer> aStack = df.pathTo(1);
        while (!aStack.isEmpty()) {
            System.out.print(aStack.pop() + "->");
        }
        System.out.println("end");*/

        df.bfs(0);
        for (int i = 0; i < 6; i++) {
            System.out.println(df.marked(i));
        }
        Stack<Integer> aStack = df.pathTo(4);
        while (!aStack.isEmpty()) {
            System.out.print(aStack.pop() + "->");
        }
        System.out.println("end");
    }
}

/*
 * 图处理dispose
 */
class DisposeMap {
    private boolean[] marked; //将已经搜素过的节点储存为true
    private int count = 0;
    private Graph G;
    private int s; //起点
    private int[] edgeTo; //edgeTo[w] = v，w为图中的节点，v为它的父节点

    public DisposeMap(Graph G) {
        this.G = G;

        marked = new boolean[G.V];
        edgeTo = new int[G.V];
        for (int i = 0; i < marked.length; i++) {
            marked[i] = false;
        }
    }
    /*
     * 深度优先搜索,储存以s为起点所能到达的所有点
     */
    public void dfs(int s) {
        marked[s] = true;

        count++;
        System.out.println("Search" + s);
        for (Integer b : G.adj(s)) { //搜索一个节点的相邻的第一个没有被标记过的节点
            if (marked[b] == false) { //如果没有搜索过这个节点，就搜索它
                edgeTo[b] = s;
                dfs(b);
            }
        }
    }
    /*
     * 广度优先搜索
     */
    public void bfs(int s) {
        edu.princeton.cs.algs4.Queue<Integer> queue = new Queue<Integer>();
        queue.enqueue(s);
        marked[s] = true;

        while (!queue.isEmpty()) {
            Integer temp = queue.dequeue();
            for (Integer b : G.adj(temp)) { //搜索一个节点的所有的相邻的节点
                if (marked[b] == false) { //如果没有搜索过这个节点，就搜索它
                    queue.enqueue(b);
                    edgeTo[b] = temp;
                    marked[b] = true;
                }
            }
        }
    }
    /*
     * 查看某点是否被标记
     */
    public boolean marked(int w) { return marked[w];}
    /*
     * 搜索了几个点
     */
    public int count() { return count;}
    /*
     * 是否存在s到v的路径
     */
    public boolean hasPathTo(int v) {
        return marked(v);
    }
    /*
     * s到v的路径，有则返回一个Stack，没有则返回null
     */
    public Stack<Integer> pathTo(int v) {
        Stack<Integer> a = new Stack<Integer>();
        for (int i = v; i != s; i = edgeTo[i])
            a.push(i);
        a.push(s);
        return a;
    }
}

/*
 * 图
 */
class Graph {
    Bag<Integer>[] graph; //这里使用背包的数组，邻借表
    int V;
    int E;

    public Graph(int V) {
        this.V = V;
        graph = (Bag<Integer>[]) new Bag[V];
        for (int i = 0; i < graph.length; i++) {
            graph[i] = (Bag<Integer>) new Bag();
        }
    }
    /*
     * 返回顶点数
     */
    public int V() { return V;}
    /*
     * 返回边数
     */
    public int E() { return E;}
    /*
     * 向图中添加一条边
     */
    public void addEdge(int v, int w) {
        graph[v].add(w);
        graph[w].add(v);
        E++;
    }
    /*
     * 和v相邻的所有顶点
     */
    public Iterable<Integer> adj(int v) {
        return graph[v];
    }
    /*
     * 计算v的度数
     */
    public static int degree(Graph G, int v) {
        int degree = 0;
        for (Integer bag : G.graph[v]) degree++;
        return degree;
    }
    @Override
    public String toString() {
        String s = V + " vertices, " + E + " edges\n";
        for (int v = 0; v < V; v++) {
            s += v + ": ";
            for (Integer integer : this.adj(v)) {
                s += integer + " ";
            }
            s += "\n";
        }
        return s;
    }
}

/*
 * 背包
 */
class Bag<T> implements Iterable<T> {
    Node first;

    private class Node {
        T value;
        Node next;
    }

    public void add(T value) {
        Node oldfirst = first;
        first = new Node();
        first.value = value;
        first.next = oldfirst;
    }

    public void delete(T value) {

    }

    @Override
    public Iterator<T> iterator() {
        return new BagIterator();
    }

    private class BagIterator implements Iterator<T> {
        Node node = first;

        @Override
        public boolean hasNext() {
            return node != null;
        }

        @Override
        public T next() {
            T tempt = node.value;
            node = node.next;
            return tempt;
        }
    }
}

代码中的无向图

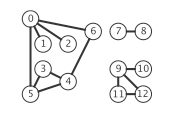
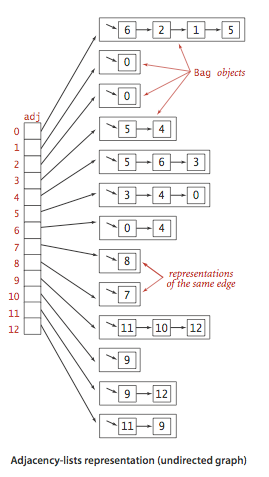
图的储存-邻接表示意图