【机器学习】彻底搞懂CNN

之前通过各种博客视频学习CNN，总是对参数啊原理啊什么的懵懵懂懂。。这次上课终于弄明白了，O(∩_∩)O~

上世纪科学家们发现了几个视觉神经特点，视神经具有局部感受野，一整张图的识别由多个局部识别点构成；不同神经元对不同形状有识别能力，且视神经具有叠加能力，高层复杂的图案可以由低层简单线条组成。之后人们发现经过conclusional的操作，可以很好反映视神经处理计算的过程，典型的是1998年LeCun发明的LeNet-5，可以极大地提升识别效果。

本文主要就convolutional layer、pooling layer和整体CNN结构展开

一、Convolutional Layer卷积层

1、原理和参数

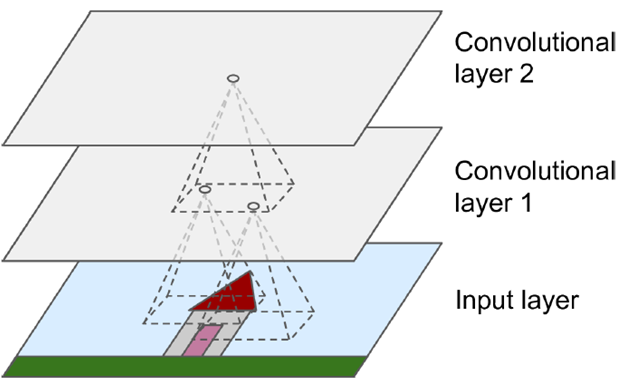
可以模拟局部感受野的性质，同上一层不是全连接，而是一小块区域连接，这一小块就是局部感受野（receptive field）。并且通过构造特定的卷积神经元，可以模拟不同神经元对不同形状刺激不同反应的性质。如下图所示，一个神经元处理一层会形成一个feature map，多层叠加，层数逐渐加深。

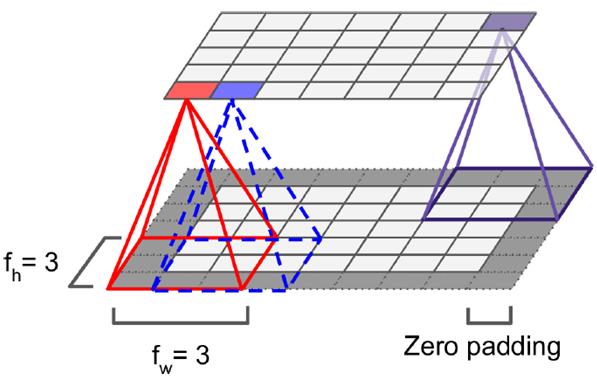
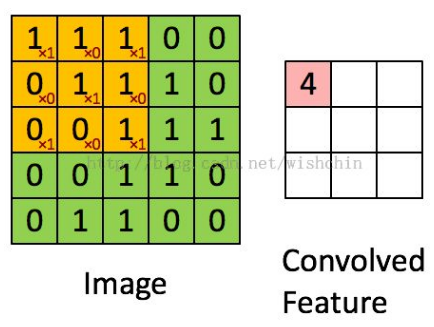
感受野（kernel或filter）的尺寸可以看做fh*fw，由于感受野本身具有尺寸，feature map会不断缩小，为了处理方便，使得每层大小不变，于是我们每层加值为0的边（zero padding），保证经过处理以后的feature map同前一层尺寸一样。多层之间的卷积运算操作，相当于和原来像素对应位置做乘法。如下左图所示，加了边后可以保证上下层大小一致，右图表示每层之间convolve的操作（如果不加zero padding）。

但上图所示只是简单例子，一般扫描的是三维图像（RGB），就不是一个矩阵，而是一个立方体，我们用一个三维块去扫描它，原理同上图相同。

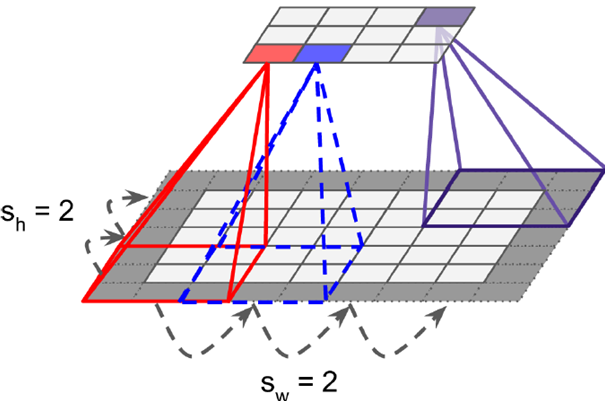
有时扫描时不是顺序去扫，而是跳跃着扫描，每次移动2-3个像素值（stride），但并非完全分离不会造成信息丢失，这样形成的feature map相较于原始图片缩小，实现信息聚集的效果。

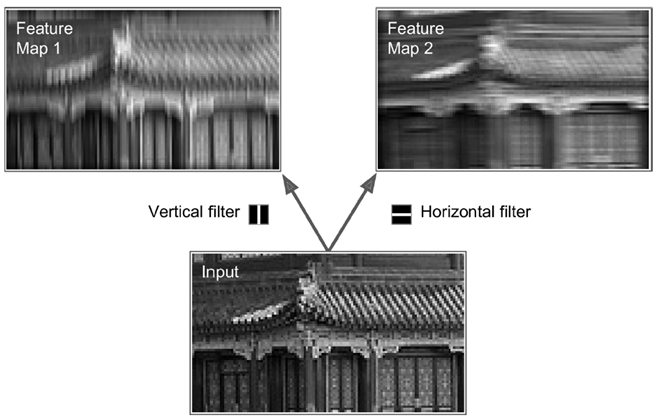
就像如下灰度图（2d）中所示，左边只提取竖线（vertical filter），右边只提取横线（horizontal filter）可看出横梁部分变亮，大量不同的这样的filter（比如可以识别边角、折线的filter）的叠加，可形成多张feature maps

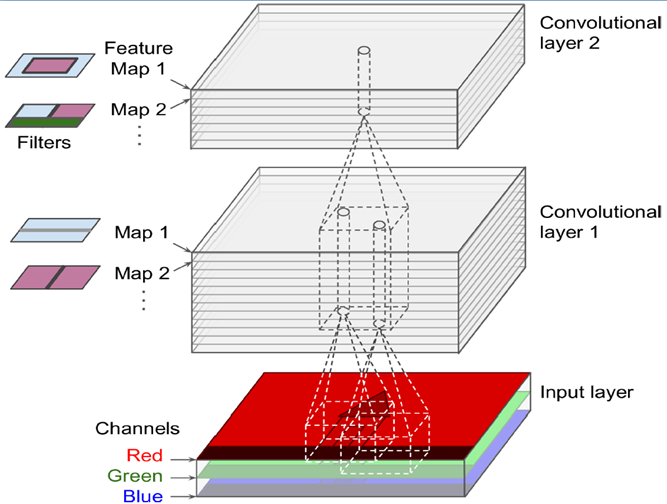
下图是一个3d的RGB效果，每个kernel（filter）可以扫描出一张feature map，多个filter可以叠加出很厚的feature maps，前一层filter做卷积可以形成后一层的一个像素点

如下图，可以代表i行j列k深度的一个输出像素值，k’代表第k个filter，w代表filter中的值，x代表输入，b是偏值。

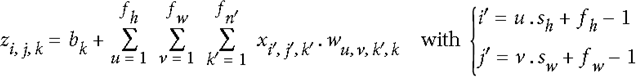
2、TensorFlow实现

以下是使用TensorFlow实现的代码，主要使用conv2d这个函数

import numpy as np
from sklearn.datasets import load_sample_images
# Load sample images
dataset = np.array(load_sample_images().images, dtype=np.float32)
# 一共4维，channel表示通道数，RGB是3
batch_size, height, width, channels = dataset.shape
# Create 2 filters
# 一般感受野大小7*7,5*5,3*3，设置2个kernel，输出2层feature map
filters_test = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
# 第一个（0）filter的设定，7*7矩阵中，3是中间
filters_test[:, 3, :, 0] = 1 # vertical line
# 第二个（1）filter的设定
filters_test[3, :, :, 1] = 1 # horizontal line
# a graph with input X plus a convolutional layer applying the 2 filters
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
# 虽然输入是一个四维图像，但是由于batch_size和channel都已经固定，所以使用conv2d
# strides设定，第一个和第四个都是1表示不可以跳过batch_size和channel
# 那两个2表示横纵向都缩减2，相当于整张图片缩减为原来四分之一，做了75%的缩减
convolution = tf.nn.conv2d(X, filters, strides=[1,2,2,1], padding="SAME")
with tf.Session() as sess:
    output = sess.run(convolution, feed_dict={X: dataset})

下面是padding的值SAME和VALID的区别（filter的宽度为6，stride为5），SAME确保所有图像信息都被convolve添加zero padding，而VALID只添加包含在内的像素点

3、所耗内存计算

相比于传统的全连接层，卷积层只是部分连接，节省了很多内存。

比如：一个具有5*5大小filter的卷积层，输出200张150*100大小的feature maps，stride取1（即不跳跃），padding为SAME。输入是150*100大小的RGB图像（channel=3），总共的参数个数是200*（5*5*3+1）=15200，其中+1是bias；如果输出采用32-bits float表示（np.float32），那么每张图片会占据200*150*100*32=9600000bits（11.4MB），如果一个training batch包含100张图片（mini-batch=100），那么这一层卷积层就会占据1GB的RAM。

可以看出，训练卷积神经网络是非常消耗内存的，但是使用时，只用到最后一层的输出即可。

二、Pooling Layer池化层

1、原理和参数

当图片大小很大时内存消耗巨大，而Pooling Layer所起的作用是浓缩效果，缓解内存压力。

即选取一定大小区域，将该区域用一个代表元素表示。具体的Pooling有两种，取平均值（mean）和取最大值（max）。如下图所示是一个取最大值的pooling layer，kernel大小为2*2，stride大小取决于kernel大小，这里是2，即刚好使得所有kernel都不重叠的值，因而实现高效的信息压缩，将原始图像横纵压缩一半，如右图所示，特征基本都完全保留了下来。

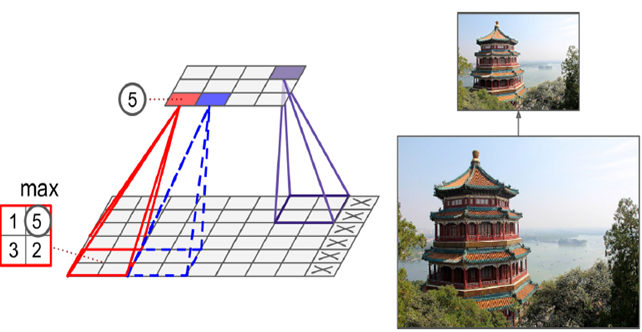
pooling这个操作不影响channel数，在feature map上也一般不做操作（即z轴一般不变），只改变横纵大小。

2、TensorFlow实现

# Create a graph with input X plus a max pooling layer
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
# 选用取最大值的max_pool方法
# 如果是取平均值，这里是mean_pool
# ksize就是kernel大小，feature map和channel都是1,横向纵向是2
max_pool = tf.nn.max_pool(X, ksize=[1,2,2,1], strides=[1,2,2,1],padding="VALID")

with tf.Session() as sess:
    output = sess.run(max_pool, feed_dict={X: dataset})

三、整体CNN框架

典型CNN architecture

有名的CNN架构：

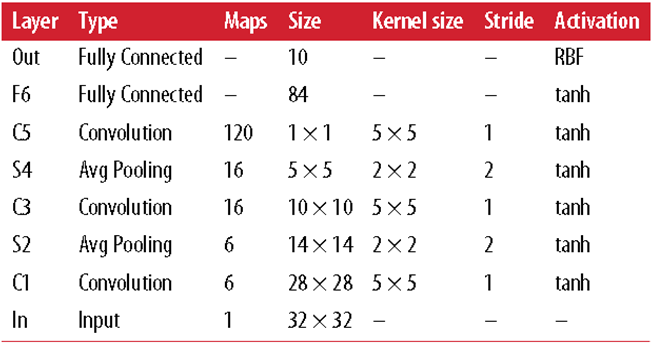
LeNet（MISIT上）-1998：输入32*32（在28*28图像上加了zero padding）。第一层kernel用了6个神经元，kernel大小5*5，stride取1，输出就是28*28；第二层做了average pooling，2*2的kernel，stride是2，输出就变为原来的一半，不改变feature map数目；第三层放了16个神经元，其他同理；第五层用了120个神经元，5*5的kernel对5*5的输入做卷积，没法再滑动，输出为1*1；F6用120个1*1的输出全连接84个神经元，Out全连接10个神经元，对应手写体识别输出的10个数字。

激活函数前面都用的tanh，是传统CNN中常用的，输出层用了RBF比较特殊，是一个计算距离的方式去判断和目标输出间距离做lost。。

AlexNet-2012：最早应用于竞赛中，近10%的提高了准确度

输入224*224的彩色图像，C1是个很大的11*11的filter，stride=4。。最后连做3层convolution。。最后输出1000个类的分类结果。

激活函数使用ReLU，这在现今很流行，输出层用的softmax

AlexNet使用了一个小技巧是Local Response Normalization（LRN局部响应归一化）

这种操作可以在传统输出上加一个bias，考虑到近邻的一些输出影响。即一个输出旁边有很牛掰的输出的话，它的输出就会怂了，收到抑制，可以看到，含β的整个项都在分母上。但后来发现，这个技术对分类器的提升也不是很明显，有的就没有用。

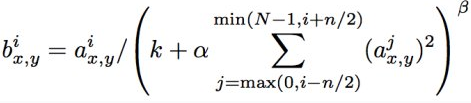
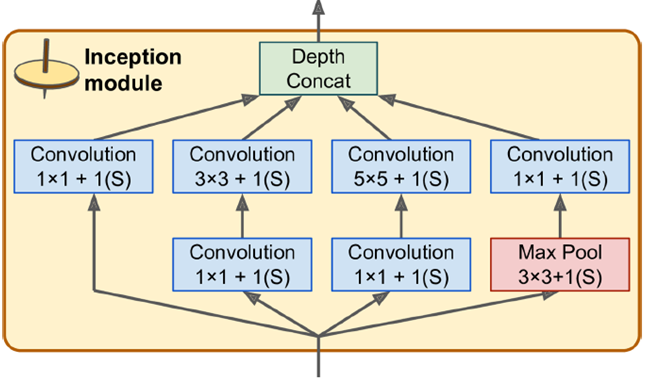
GoogleLeNet-2014：

大量应用Inception module，一个输入进来，直接分四步进行处理，这四步处理完后深度直接进行叠加。在不同的尺度上对图片进行操作。大量运用1*1的convolution，可以灵活控制输出维度，可以降低参数数量。

如右图所示，输入是192，使用了9层inception module，如果直接用3*3,5*5参数，可以算一下，之后inception参数数目是非常大的，深度上可以调节，可以指定任意数目的feature map，通过增加深度把维度减下来。inception模块6个参数刚好对应这6个convolution，上面4个参数对应上面4个convolution，加入max pool不会改变feature map数目（如480=128+192+96+64）。

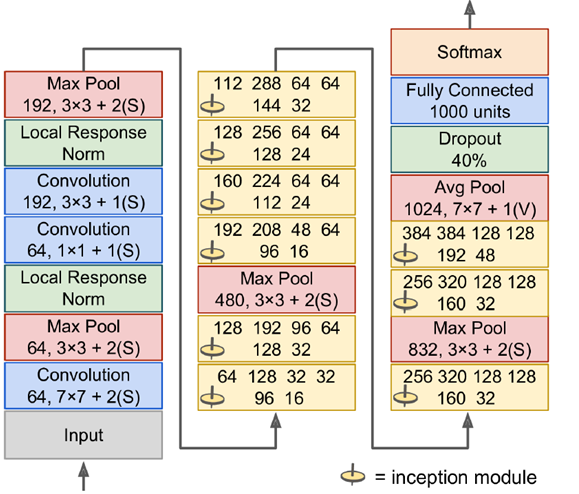
将正确率升高到95-96%，超过人类分辨率，因为image net中但是狗的种类就有很多，人类无法完全一一分辨出。

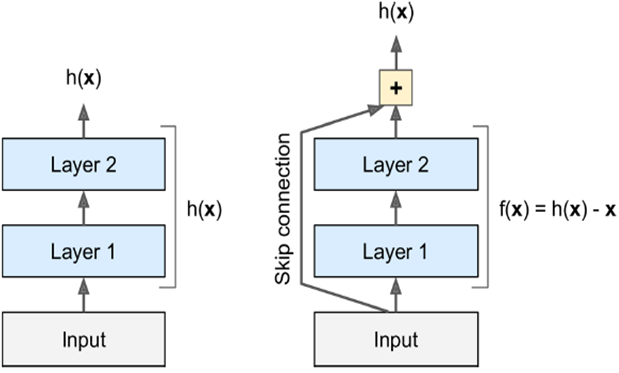
ReSNet残差网络-2015：

不再直接学习一个目标函数，输入直接跳过中间层直接连到输出上，要学习的是残差f（x），输入跳过中间层直接加到输出上。

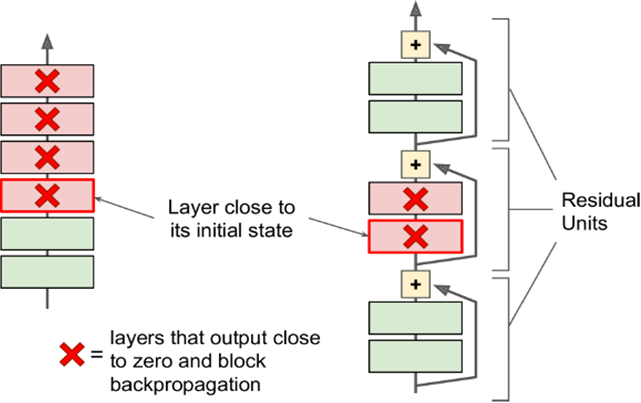
好处是：深度模型路径依赖的限制，即gradient向前传导时要经过所有层，如果中间有层死掉了，前面的层就无法得到训练。残差网络不断跳跃，即使中间有的层已经死掉，信息仍旧能够有效流动，使得训练信号有效往回传导。