V-rep学习笔记：机器人逆运动学数值解法（The Jacobian Transpose Method）

　　机器人运动学逆解的问题经常出现在动画仿真和工业机器人的轨迹规划中：We want to know how the upper joints of the hierarchy would rotate if we want the end effector to reach some goal.

IK Solutions：

• Analytical solutions are desirable because of their speed and exactness of solution.
• For complex kinematics problems, analytical solutions may not be possible.
• Use iterative methods (迭代法)--Optimization methods (e.g., minimize the distance between end effector and goal point)

　　机器人学的教材上一般只介绍了运动学逆解的解析解法，很少涉及数值解（迭代解法）。其中有两方面的原因，一是数值解相对于解析解需要的运算量更大，不太适合实时性要求较高的场合；另一方面是因为一般在设计机器人的结构时就会考虑其逆解的可解性，比如相邻的三个关节轴线相交即存在解析解。下面以最简单的二连杆机构为例子，研究一下机器人运动学逆解的数值解法。如下图所示，其运动学正解很容易得到，根据运动学正解可以写出机器人的雅克比矩阵J。

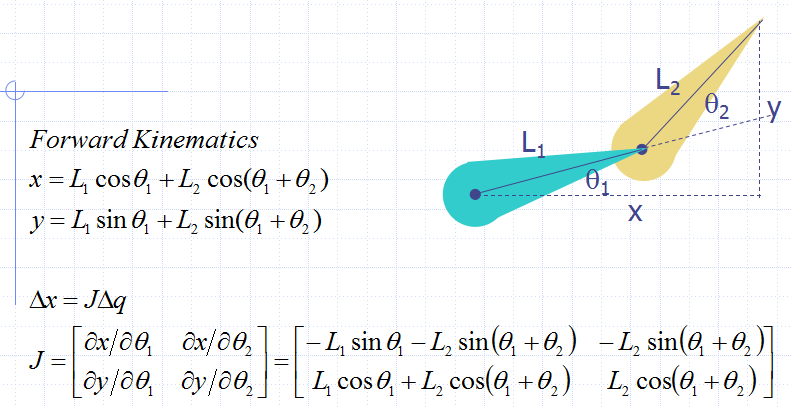
What is Jacobian? A linear approximation to f(x). 雅克比矩阵相当于函数f(x)的一阶导数，即线性近似。

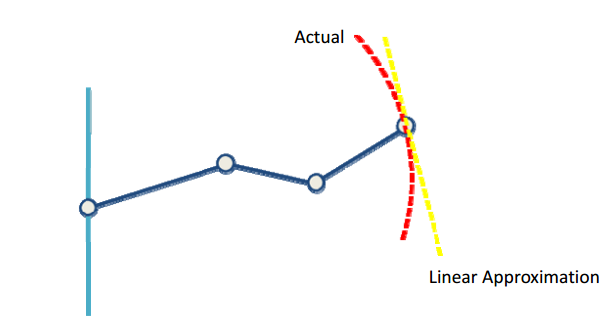
Computing the Jacobian Numerically:（雅克比矩阵的计算有解析法和数值法，当难以根据解析法得到雅克比时可以用差分法代替微分求解）

下面是Jacobian Transpose方法的主要推导过程：

　　It is recommended that you choose a small positive scalar α < 1 and update the joint angles θ by adding Δθ. Then proceed iteratively by recomputing the Jacobian based on the updated angles and positions, finding new values for Δθ and again updating with a small fraction α. This is repeated until the links are sufficiently close to the desired positions. The question of how small α needs to be depends on the geometry of the links; it would be a good idea to keep α small enough so that the angles are updated by at most 5 or 10° at a time.

　　这一方法运用了最速降法（梯度法）的思想，利用目标函数在迭代点的局部性态，每步搜索都沿着函数值下降最快的方向，即负梯度方向进行搜索。迭代过程的几何概念较为直观，方法和程序简单，容易实现，不足之处是每次迭代都是沿着迭代点的负梯度方向搜索，搜索路径较为曲折，收敛慢。

Operating Principle:  

Project difference vector DX on those dimensions qwhich can reduce it the most. It is a plausible, justifyable approach, because it is related to the method of steepest decent.( It follows a force that pulls the end-effector towards its desired target location).

Advantages:
1. Simple computation (numerically robust)
2. No matrix inversions

Disadvantages:
1. Needs many iterations until convergence in certain configurations 
2. Unpredictable joint configurations
3. Non conservative

　　下面以V-rep中官方自带的例子（在文件夹scenes/ik_fk_simple_examples中）为基础进行修改，添加代码手动实现运动学逆解的求解。为了实现同样的功能先将两个旋转关节从Inverse kinematics mode设为Passive mode，然后将target和tip的Linked dummy设为none，并在Calculation Modules的Inverse kinematics选项卡中取消IK groups enabled。下图中红色的dummy为target dummy，仿真开始后程序会计算连杆末端（tip dummy）与target之间的误差，然后根据Jacobian Transpose方法不断计算关节调整量，直到误差小于容许值。

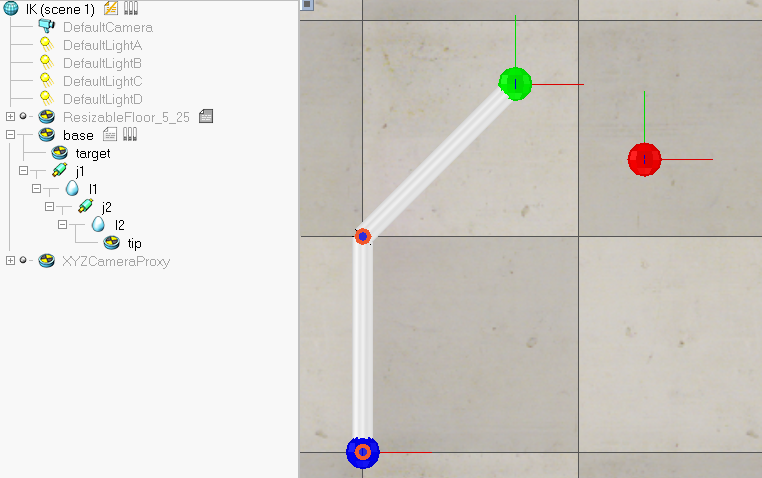
　　如下图所示，迭代计算61次收敛后，点击图中的Compute IK按钮，连杆末端能根据计算出的关节角q1,q2移动到target的位置（可以随意拖动target的位置，在合理的范围内经过逆解计算tip都会与target重合）

在child script中由lua API实现了该方法

if (sim_call_type==sim_childscriptcall_initialization) then
    ui=simGetUIHandle('UI')
    J1_handle = simGetObjectHandle('j1')
    J2_handle = simGetObjectHandle('j2')
    target_handle = simGetObjectHandle('target')
    consoleHandle = simAuxiliaryConsoleOpen('info', , +, {,},{,})

    --link length
    L1 = 0.5
    L2 = 0.5

    gamma =        --step size
    stol = 1e-2     --tolerance
    nm =         --initial error
    count =        --iteration count
    ilimit =    --maximum iteratio

    --initial joint value
    q1 =
    q2 =
end

if (sim_call_type==sim_childscriptcall_actuation) then
    local a=simGetUIEventButton(ui)
    local target_pos = simGetObjectPosition(target_handle, -)

    if(nm > stol)
    then
        simAuxiliaryConsolePrint(consoleHandle, nil)

        local x, y = L1*math.cos(q1)+L2*math.cos(q1+q2), L1*math.sin(q1)+L2*math.sin(q1+q2)
        local delta_x, delta_y = target_pos[] - x, target_pos[] - y
        local dq_1 = (-L1*math.sin(q1)-L2*math.sin(q1+q2))*delta_x + (L1*math.cos(q1)+L2*math.cos(q1+q2))*delta_y
        local dq_2 = (-L2*math.sin(q1+q2))*delta_x + (L2*math.cos(q1+q2))*delta_y
        q1, q2 = q1 + gamma*dq_1,  q2 + gamma*dq_2

        nm = math.sqrt(delta_x * delta_x + delta_y * delta_y)

        count = count +
        if count > ilimit   then
            simAuxiliaryConsolePrint(consoleHandle,"Solution wouldn't converge\r\n")
        end

        simAuxiliaryConsolePrint(consoleHandle, string.format("q1:%.2f", q1*/math.pi)..'  '..string.format("q2:%.2f", q2*/math.pi)..'\r\n')
        simAuxiliaryConsolePrint(consoleHandle, string.format("x:%.2f",x)..'  '..string.format("y:%.2f", y)..'\r\n')
        simAuxiliaryConsolePrint(consoleHandle, string.format("%d", count)..'iterations'..'  '..string.format("err:%.4f", nm)..'\r\n')
    end

    -- if the button(a is the button handle) is pressed
    if a== then
        simSetJointPosition(J1_handle, q1+math.pi/)  -- the angle between L1 and X-axis is 90 degree
        simSetJointPosition(J2_handle, q2)
    end
end