L0/L1/L2范数的联系与区别

L0/L1/L2范数的联系与区别

标签（空格分隔）： 机器学习

---

最近快被各大公司的笔试题淹没了，其中有一道题是从贝叶斯先验，优化等各个方面比较L0、L1、L2范数的联系与区别。

L0范数

L0范数表示向量中非零元素的个数：
\(||x||_{0} = \#(i)\ with\ \ x_{i} \neq 0\)

也就是如果我们使用L0范数，即希望w的大部分元素都是0. （w是稀疏的）所以可以用于ML中做稀疏编码，特征选择。通过最小化L0范数，来寻找最少最优的稀疏特征项。但不幸的是，L0范数的最优化问题是一个NP hard问题，而且理论上有证明，L1范数是L0范数的最优凸近似，因此通常使用L1范数来代替。

L1范数 -- (Lasso Regression)

L1范数表示向量中每个元素绝对值的和：
\(||x||_{1} = \sum_{i=1}^{n}|x_{i}|\)

L1范数的解通常是稀疏性的，倾向于选择数目较少的一些非常大的值或者数目较多的insignificant的小值。

L2范数 -- (Ridge Regression)

L2范数即欧氏距离：
\(||x||_{2} = \sqrt{\sum_{i=1}^{n}x_{i}^{2}}\)

L2范数越小，可以使得w的每个元素都很小，接近于0，但L1范数不同的是他不会让它等于0而是接近于0.

L1范数与L2范数的比较：

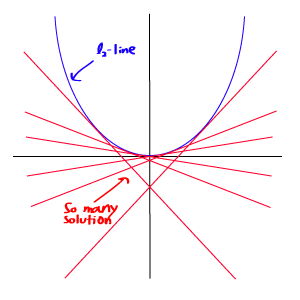
但由于L1范数并没有平滑的函数表示，起初L1最优化问题解决起来非常困难，但随着计算机技术的到来，利用很多凸优化算法使得L1最优化成为可能。

贝叶斯先验

从贝叶斯先验的角度看，加入正则项相当于加入了一种先验。即当训练一个模型时，仅依靠当前的训练数据集是不够的，为了实现更好的泛化能力，往往需要加入先验项。

• L1范数相当于加入了一个Laplacean先验；
• L2范数相当于加入了一个Gaussian先验。
  如下图所示：
  

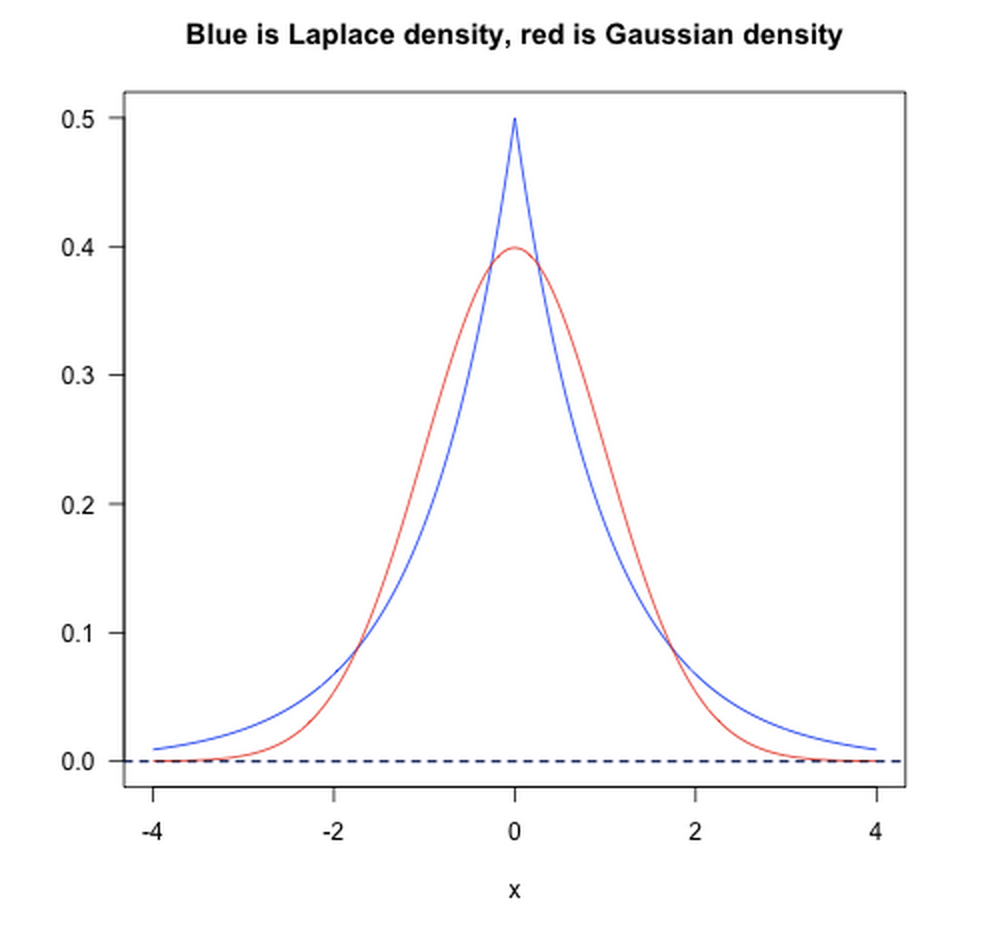
【Reference】
1. http://blog.csdn.net/zouxy09/article/details/24971995
2. http://blog.sciencenet.cn/blog-253188-968555.html
3. http://t.hengwei.me/post/%E6%B5%85%E8%B0%88l0l1l2%E8%8C%83%E6%95%B0%E5%8F%8A%E5%85%B6%E5%BA%94%E7%94%A8.html