NeHe OpenGL教程 第三十课：碰撞检测

转自【翻译】NeHe OpenGL 教程

前言

声明，此 NeHe OpenGL教程系列文章由51博客yarin翻译（2010-08-19），本博客为转载并稍加整理与修改。对NeHe的OpenGL管线教程的编写，以及yarn的翻译整理表示感谢。

NeHe OpenGL第三十课：碰撞检测

碰撞检测:

这是一课激动的教程，你也许等待它多时了。你将学会碰撞剪裁，物理模拟太多的东西，慢慢期待吧。

 

碰撞检测和物理模拟(作者:Dimitrios Christopoulos (christop@fhw.gr))

碰撞检测

这是一个我遇到的最困难的题目,因为它没有一个简单的解决办法.对于每一个程序都有一种检测碰撞的方法.当然这里有一种蛮力,它适用于各种不同的应用,当它非常的费时.

我们将讲述一种算法,它非常的快,简单并易于扩展.下面我们来看看这个算法包含的内容:

1) 碰撞检测

移动的球-平面

移动的球-圆柱

移动的球-移动的球

2) 基于物理的建模

碰撞表示

应用重力加速度

3) 特殊效果

爆炸的表示，利用互交叉的公告板形式

声音使用Windows声音库

4) 关于代码

代码被分为以下5个部分

Lesson30.cpp   : 主程序代码l

Image.cpp, Image.h : 加载图像

Tmatrix.cpp, Tmatrix.h : 矩阵

Tray.cpp, Tray.h : 射线

Tvector.cpp, Tvector.h : 向量

1) 碰撞检测

我们使用射线来完成相关的算法，它的定义为:

射线上的点 = 射线的原点+ t * 射线的方向

t 用来描述它距离原点的位置，它的范围是[0, 无限远).

现在我们可以使用射线来计算它和平面以及圆柱的交点了。

射线和平面的碰撞检测：

平面被描述为：

Xn dot X = d

Xn 是平面的法线.

X 是平面上的一个点.

d 是平面到原点的距离.

现在我们得到射线和平面的两个方程:

PointOnRay = Raystart + t * Raydirection

Xn dot X = d

如果他们相交，则上诉方程组有解，如下所示：

Xn dot PointOnRay = d

(Xn dot Raystart) + t * (Xn dot Raydirection) = d

解得 t:

t = (d - Xn dot Raystart) / (Xn dot Raydirection)

t代表原点到与平面相交点的参数,把t带回原方程我们会得到与平面的碰撞点.如果Xn*Raydirection=0。则说明它与平面平行，则将不产生碰撞。如果t为负值，则说明交点在射线的相反方向，也不会产生碰撞。

 

//判断是否和平面相交，是则返回1，否则返回0int TestIntersionPlane(const Plane&
plane,const TVector& position,const TVector& direction,
double& lamda, TVector&

pNormal){

double DotProduct=direction.dot(plane._Normal);

double l2;

//判断是否平行于平面

if ((DotProduct<ZERO)&&(DotProduct>-ZERO))

return 0;

l2=(plane._Normal.dot(plane._Position-position))/DotProduct;

if (l2<-ZERO)

return 0;

pNormal=plane._Normal;

lamda=l2;

return 1;

}

射线-圆柱的碰撞检测

计算射线和圆柱方程组得解。 

  

int TestIntersionCylinder(const Cylinder& cylinder,const
TVector& position,const TVector& direction, double& lamda,
TVector& pNormal,TVector& newposition)

球-球之间的碰撞检测

球被表示为中心和它的半径，决定两个球是否相交就是求出它们之间的距离是否小于它们的直径。

在处理两个移动的球是否相交时，有一个bug就是，当它们的移动速度太快，回出现它们相交，但在相邻的两步检测不出它们是否相交的情况，如下图所示：

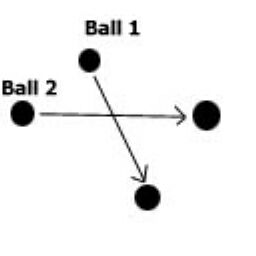
有一个替代的办法就是细分相邻的时间片断，如果在这之间发生了碰撞，则确定有效。我们把这个细分时间段设置为3，代码如下：  

  

//判断球和球是否相交，是则返回1，否则返回0int FindBallCol(TVector& point, double&
TimePoint, double Time2, int& BallNr1, int& BallNr2){ TVector
RelativeV; TRay rays; double MyTime=0.0, Add=Time2/150.0,
Timedummy=10000, Timedummy2=-1; TVector posi;  //判断球和球是否相交 for (int
i=0;i<NrOfBalls-1;i++) {  for (int j=i+1;j<NrOfBalls;j++)  {

RelativeV=ArrayVel[i]-ArrayVel[j];   rays=TRay(OldPos[i],TVector::unit(RelativeV));   MyTime=0.0;

if ( (rays.dist(OldPos[j])) > 40) continue;

while (MyTime<Time2)

{

MyTime+=Add;

posi=OldPos[i]+RelativeV*MyTime;

if (posi.dist(OldPos[j])<=40) {

point=posi;

if (Timedummy>(MyTime-Add)) Timedummy=MyTime-Add;

BallNr1=i;

BallNr2=j;

break;

}

}

}

}

if (Timedummy!=10000) { TimePoint=Timedummy;

return 1;

}

return 0;

}

怎样应用我们的知识

现在我们已经可以决定射线和平面/圆柱的交点了,如下图所示:

当我们找到了碰撞位置后,下一步我们需要知道它是否发生在当前这一步中.如果距离碰撞点的位置小于这一步球体运动的间隔,则碰撞发生.我们使用如下的方程计算运动到碰撞时所需的时间:

Tc= Dsc*T / Dst

接着我们知道碰撞点位置,如下面公式所示:

Collision point= Start + Velocity*Tc

2) 基于物理的模拟

碰撞反应

为了计算对于一个静止物体的碰撞,我们需要知道以下信息:碰撞点,碰撞法线,碰撞时间.

它是基于以下物理规律的,碰撞的入射角等于反射角.如下图所示:

R 为反射方向

I 为入射方向

N 为法线方向

反射方向有以下公式计算 :

R= 2*(-I dot N)*N + I

 

rt2=ArrayVel[BallNr].mag();      // 返回速度向量的模

ArrayVel[BallNr].unit();      // 归一化速度向量

// 计算反射向量

ArrayVel[BallNr]=TVector::unit( (normal*(2*normal.dot(-ArrayVel[BallNr]))) + ArrayVel[BallNr] );

ArrayVel[BallNr]=ArrayVel[BallNr]*rt2;

球体之间的碰撞

由于它很复杂，我们用下图来说明这个原理. 



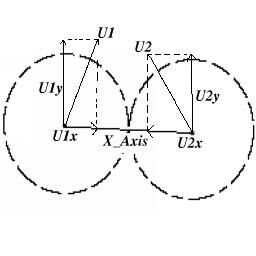
U1和U2为速度向量，我们用X_Axis表示两个球中心连线的轴，U1X和U2X为U1和U2在这个轴上的分量。U1y和U2y为垂直于X_Axis轴的分量。M1和M2为两个球体的分量。V1和V2为碰撞后的速度，V1x,V1y,V2x,V2y为他们的分量。

在我们的例子里，所有球的质量都相等，解得方程为，在垂直轴上的速度不变，在X_Axis轴上互相交换速度。代码如下：

 

TVector pb1,pb2,xaxis,U1x,U1y,U2x,U2y,V1x,V1y,V2x,V2y;

double a,b;

pb1=OldPos[BallColNr1]+ArrayVel[BallColNr1]*BallTime;   // 球1的位置

pb2=OldPos[BallColNr2]+ArrayVel[BallColNr2]*BallTime;   // 球2的位置

xaxis=(pb2-pb1).unit();       // X-Axis轴

a=xaxis.dot(ArrayVel[BallColNr1]);     // X_Axis投影系数

U1x=xaxis*a;        // 计算在X_Axis轴上的速度

U1y=ArrayVel[BallColNr1]-U1x; // 计算在垂直轴上的速度

xaxis=(pb1-pb2).unit();       

b=xaxis.dot(ArrayVel[BallColNr2]);     

U2x=xaxis*b;        

U2y=ArrayVel[BallColNr2]-U2x;

V1x=(U1x+U2x-(U1x-U2x))*0.5;      // 计算新的速度

V2x=(U1x+U2x-(U2x-U1x))*0.5;

V1y=U1y;

V2y=U2y;

for (j=0;j<NrOfBalls;j++)      // 更新所有球的位置

ArrayPos[j]=OldPos[j]+ArrayVel[j]*BallTime;

ArrayVel[BallColNr1]=V1x+V1y;      // 设置新的速度

ArrayVel[BallColNr2]=V2x+V2y;      

  

万有引力的模拟

我们使用欧拉方程来模拟万有引力，如下所示：

Velocity_New = Velovity_Old + Acceleration*TimeStep

Position_New = Position_Old + Velocity_New*TimeStep

在每次模拟中，我们用上面公式计算的速度取代旧的速度

3) 特殊效果

爆炸

最好的表示爆炸效果的就是使用两个互相垂直的平面，并使用alpha混合在窗口中显示它们。接着让alpha变为0，设定爆炸效果不可见。代码如下所示： 

  

// 渲染/混合爆炸效果

glEnable(GL_BLEND);       // 使用混合

glDepthMask(GL_FALSE);       // 禁用深度缓存

glBindTexture(GL_TEXTURE_2D, texture[1]);    // 设置纹理

for(i=0; i<20; i++)       // 渲染20个爆炸效果

{

 if(ExplosionArray[i]._Alpha>=0)

 {

  glPushMatrix();

  ExplosionArray[i]._Alpha-=0.01f;   // 设置alpha

  ExplosionArray[i]._Scale+=0.03f;   // 设置缩放

  // 设置颜色

  glColor4f(1,1,0,ExplosionArray[i]._Alpha);  

  glScalef(ExplosionArray[i]._Scale,ExplosionArray[i]._Scale,ExplosionArray[i]._Scale);

  // 设置位置

  glTranslatef((float)ExplosionArray[i]._Position.X()/ExplosionArray[i]._Scale,

   (float)ExplosionArray[i]._Position.Y()/ExplosionArray[i]._Scale,

   (float)ExplosionArray[i]._Position.Z()/ExplosionArray[i]._Scale);

  glCallList(dlist);     // 调用显示列表绘制爆炸效果

  glPopMatrix();

 }

}

声音

在Windows下我们简单的调用PlaySound()函数播放声音。

4) 代码的流程

如果你成功的读完了理论部分，在你开始运行程序并播放声音以前。我们将用伪代码向你介绍一些整个流程，以便你能成功的看懂代码。 

  

While (Timestep!=0)

{

 对每一个球

 {

  计算最近的与平面碰撞的位置;

  计算最近的与圆柱碰撞的位置;

  如果碰撞发生，则保存并替换最近的碰撞点;

 }

 检测各个球之间的碰撞;

 如果碰撞发生，则保存并替换最近的碰撞点;

If (碰撞发生)

 {

  移动所有的球道碰撞点的时间;

  (We already have computed the point, normal and collision time.)

  计算碰撞后的效果;

  Timestep-=CollisonTime;

 }

 else

  移动所有的球体一步

}

下面是对上面伪代码的实现：

 

//模拟函数，计算碰撞检测和物理模拟void idle(){  double rt,rt2,rt4,lamda=10000;  TVector
norm,uveloc;  TVector normal,point,time;  double RestTime,BallTime; 
TVector Pos2;  int BallNr=0,dummy=0,BallColNr1,BallColNr2;  TVector Nc;

//如果没有锁定到球上，旋转摄像机

if (!hook_toball1)

{

camera_rotation+=0.1f;

if (camera_rotation>360)

camera_rotation=0;

}

RestTime=Time;

lamda=1000;

//计算重力加速度

for (int j=0;j<NrOfBalls;j++)

ArrayVel[j]+=accel*RestTime;

//如果在一步的模拟时间内(如果来不及计算，则跳过几步)

while (RestTime>ZERO)

{

lamda=10000;

//对于每个球，找到它们最近的碰撞点

for (int i=0;i<NrOfBalls;i++)

{

//计算新的位置和移动的距离

OldPos[i]=ArrayPos[i];

TVector::unit(ArrayVel[i],uveloc);

ArrayPos[i]=ArrayPos[i]+ArrayVel[i]*RestTime;

rt2=OldPos[i].dist(ArrayPos[i]);

//测试是否和墙面碰撞

if (TestIntersionPlane(pl1,OldPos[i],uveloc,rt,norm))

{

//计算碰撞的时间

rt4=rt*RestTime/rt2;

//如果小于当前保存的碰撞时间，则更新它

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=OldPos[i]+uveloc*rt;

lamda=rt4;

BallNr=i;

}

}

}

if (TestIntersionPlane(pl2,OldPos[i],uveloc,rt,norm))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=OldPos[i]+uveloc*rt;

lamda=rt4;

BallNr=i;

dummy=1;

}

}

}

if (TestIntersionPlane(pl3,OldPos[i],uveloc,rt,norm))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=OldPos[i]+uveloc*rt;

lamda=rt4;

BallNr=i;

}

}

}

if (TestIntersionPlane(pl4,OldPos[i],uveloc,rt,norm))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=OldPos[i]+uveloc*rt;

lamda=rt4;

BallNr=i;

}

}

}

if (TestIntersionPlane(pl5,OldPos[i],uveloc,rt,norm))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=OldPos[i]+uveloc*rt;

lamda=rt4;

BallNr=i;

}

}

}

//测试是否与三个圆柱相碰

if (TestIntersionCylinder(cyl1,OldPos[i],uveloc,rt,norm,Nc))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=Nc;

lamda=rt4;

BallNr=i;

}

}

}

if (TestIntersionCylinder(cyl2,OldPos[i],uveloc,rt,norm,Nc))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=Nc;

lamda=rt4;

BallNr=i;

}

}

}

if (TestIntersionCylinder(cyl3,OldPos[i],uveloc,rt,norm,Nc))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=Nc;

lamda=rt4;

BallNr=i;

}

}

}

}

//计算每个球之间的碰撞，如果碰撞时间小于与上面的碰撞，则替换它们

if (FindBallCol(Pos2,BallTime,RestTime,BallColNr1,BallColNr2))

{

if (sounds)

PlaySound("Data/Explode.wav",NULL,SND_FILENAME|SND_ASYNC);

if ( (lamda==10000) || (lamda>BallTime) )

{

RestTime=RestTime-BallTime;

TVector pb1,pb2,xaxis,U1x,U1y,U2x,U2y,V1x,V1y,V2x,V2y;

double a,b;

pb1=OldPos[BallColNr1]+ArrayVel[BallColNr1]*BallTime;

pb2=OldPos[BallColNr2]+ArrayVel[BallColNr2]*BallTime;

xaxis=(pb2-pb1).unit();

a=xaxis.dot(ArrayVel[BallColNr1]);

U1x=xaxis*a;

U1y=ArrayVel[BallColNr1]-U1x;

xaxis=(pb1-pb2).unit();

b=xaxis.dot(ArrayVel[BallColNr2]);

U2x=xaxis*b;

U2y=ArrayVel[BallColNr2]-U2x;

V1x=(U1x+U2x-(U1x-U2x))*0.5;

V2x=(U1x+U2x-(U2x-U1x))*0.5;

V1y=U1y;

V2y=U2y;

for (j=0;j<NrOfBalls;j++)

ArrayPos[j]=OldPos[j]+ArrayVel[j]*BallTime;

ArrayVel[BallColNr1]=V1x+V1y;

ArrayVel[BallColNr2]=V2x+V2y;

//Update explosion array

for(j=0;j<20;j++)

{

if (ExplosionArray[j]._Alpha<=0)

{

ExplosionArray[j]._Alpha=1;

ExplosionArray[j]._Position=ArrayPos[BallColNr1];

ExplosionArray[j]._Scale=1;

break;

}

}

continue;

}

}

//最后的测试，替换下次碰撞的时间，并更新爆炸效果的数组

if (lamda!=10000)

{

 RestTime-=lamda;

for (j=0;j<NrOfBalls;j++)

  ArrayPos[j]=OldPos[j]+ArrayVel[j]*lamda;

rt2=ArrayVel[BallNr].mag();

 ArrayVel[BallNr].unit();

 ArrayVel[BallNr]=TVector::unit( (normal*(2*normal.dot(-ArrayVel[BallNr]))) + ArrayVel[BallNr] );

 ArrayVel[BallNr]=ArrayVel[BallNr]*rt2;

for(j=0;j<20;j++)

 {

  if (ExplosionArray[j]._Alpha<=0)

  {

   ExplosionArray[j]._Alpha=1;

   ExplosionArray[j]._Position=point;

   ExplosionArray[j]._Scale=1;

   break;

  }

 }

}

else

 RestTime=0;

}

}

原文及其个版本源代码下载：

http://nehe.gamedev.net/data/lessons/lesson.asp?lesson=30