BZOJ 2039 / Luogu P1791 [2009国家集训队]employ人员雇佣 (最小割)

题面

BZOJ传送门

Luogu传送门

分析

考虑如何最小割建图,因为这仍然是二元关系,我们可以通过解方程来确定怎么建图,具体参考论文

<<浅析一类最小割问题 湖南师大附中 彭天翼>>

那么我们来看看怎么解方程



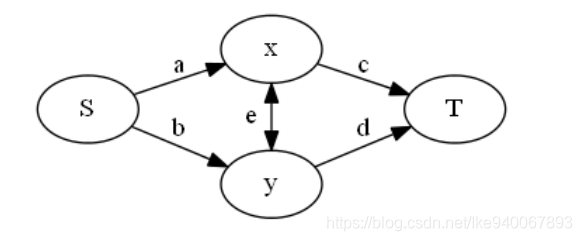
设存在一对二元关系&lt;x,y&gt;&lt;x,y&gt;<x,y>,那么假设分在SSS一边表示不雇佣,TTT一边表示雇佣.先把总收益全部加起来,那么只要考虑会每种情况会在此基础上减去多少.

• 如果两个都雇佣 : a+b=A[x]+A[y]a+b=A[x]+A[y]a+b=A[x]+A[y]
• 两个都不雇佣 : c+d=2∗E[x,y]c+d=2*E[x,y]c+d=2∗E[x,y]
• 雇佣xxx : a+d+e=3∗E[x,y]+A[x]a+d+e=3*E[x,y]+A[x]a+d+e=3∗E[x,y]+A[x]
• 雇佣yyy : b+c+e=3∗E[x,y]+A[y]b+c+e=3*E[x,y]+A[y]b+c+e=3∗E[x,y]+A[y]
  
  因为答案里已经算入x,yx,yx,y同时雇佣所带来的收益2∗E[x,y]2*E[x,y]2∗E[x,y],所以c+d=2∗E[x,y]c+d=2*E[x,y]c+d=2∗E[x,y]要减去
  
  又因为如果只雇佣一个,还会带来E[x,y]E[x,y]E[x,y]的损失,所以是3∗E[x,y]3*E[x,y]3∗E[x,y]

满足的一组解就是

a=A[x],b=A[y]a=A[x],b=A[y]a=A[x],b=A[y]

c=d=E[x,y]c=d=E[x,y]c=d=E[x,y]

e=2∗E[x,y]e=2*E[x,y]e=2∗E[x,y]

那么加上一些优化:

• 把一个点到TTT的容量全部存起来最后只连一条边;
• 最大流的一些小优化
• 其实正常情况下eee是两条边(代码实现中要存444条),但是可以直接只连一条边(代码实现中只存222条),正向边的容量为eee,反向边的容量也设为eee而不是000.快很多.
• freadfreadfread…

CODE

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
char cb[1<<15],*cs=cb,*ct=cb;
#define getc() (cs==ct && (ct = (cs = cb) + fread(cb , 1 , 1<<15 , stdin),cs==ct)?0:*cs++)
template<typename T>inline void read(T &num) {
    char ch; while((ch=getc())<'0'||ch>'9');
    for(num=0;ch>='0'&&ch<='9';num=num*10+ch-'0',ch=getc());
}

const int inf = 1e9;
const int MAXN = 1005;
const int MAXM = 2000005;
const int dx[] = { 1, -1, 0, 0, 0 };
const int dy[] = { 0, 0, -1, 1, 0 };
int n, m, fir[MAXN], S, T, cnt;
struct edge { int to, nxt; LL c; }e[MAXM];
inline void add(int u, int v, LL cc, LL rc=0) {
	e[cnt] = (edge){ v, fir[u], cc }; fir[u] = cnt++;
	e[cnt] = (edge){ u, fir[v], rc }; fir[v] = cnt++;
}
int dis[MAXN], vis[MAXN], info[MAXN], cur, q[MAXN];
inline bool bfs() {
	int head = 0, tail = 0;
	vis[S] = ++cur; q[tail++] = S;
	while(head < tail) {
		int u = q[head++];
		for(int i = fir[u]; ~i; i = e[i].nxt)
			if(e[i].c && vis[e[i].to] != cur)
				vis[e[i].to] = cur, dis[e[i].to] = dis[u] + 1, q[tail++] = e[i].to;
	}
	if(vis[T] == cur) memcpy(info, fir, (T+1)<<2);
	return vis[T] == cur;
}
LL dfs(int u, LL Max) {
	if(u == T || !Max) return Max;
	LL flow=0, delta;
	for(int &i = info[u]; ~i; i = e[i].nxt)
		if(e[i].c && dis[e[i].to] == dis[u] + 1 && (delta=dfs(e[i].to, min(e[i].c, Max-flow)))) {
			e[i].c -= delta, e[i^1].c += delta, flow += delta;
			if(flow == Max) return flow;
		}
	return flow;
}
inline LL dinic() {
	LL flow=0, x;
	while(bfs()) {
		while((x=dfs(S, inf))) flow+=x;
	}
	return flow;
}
LL sum, tmp[1005];
inline int enc(int i, int j) { return (i-1)*m + j; }
int main () {
	memset(fir, -1, sizeof fir);
	read(n); S = 0; T = n+1;
	for(int i = 1, x; i <= n; ++i)
		read(x), add(S, i, x);
	for(int i = 1, x; i <= n; ++i)
		for(int j = 1; j <= n; ++j) {
			read(x);
			if(x && i < j) {
				sum += 2ll*x, tmp[i] += x, tmp[j] += x;
				add(i, j, 2ll*x, 2ll*x);
			}
		}
	for(int i = 1; i <= n; ++i)
		if(tmp[i]) add(i, T, tmp[i]);
	printf("%lld\n", sum-dinic());
}