【原创】洛谷 LUOGU P3372 【模板】线段树1

P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

样例说明：

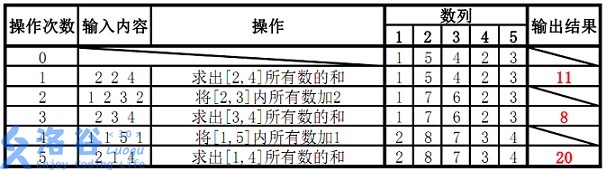
既然是模板，就不做解释了。

代码如下：

 // LUOGU 3372 【模板】线段树1
 // 2017.7.20 19:34
 #include<bits/stdc++.h>
 #define MAXN 100000
 #define MAXT MAXN*4
 using namespace std;
 int N,M,topt=;
 long long a[MAXN+];
 struct sgt_node{
     int lc,rc;
     long long sum,lazy;
 }sgt[MAXT+];
 #define lch sgt[now].lc
 #define rch sgt[now].rc
 #define smid ((l+r)>>1)
 void update(int now){
     sgt[now].sum=sgt[lch].sum+sgt[rch].sum;
 }
 void set_lazy(int now,int l,int r,long long v){
     sgt[now].sum+=(r-l+)*v;
     sgt[now].lazy+=v;
 }
 void push_down(int now,int l,int r){
     if(sgt[now].lazy){
         set_lazy(lch,l,smid,sgt[now].lazy);
         set_lazy(rch,smid+,r,sgt[now].lazy);
         sgt[now].lazy=;
     }
 }
 void Build_sgt(int &now,int l,int r){
     now=++topt;
     if(l==r){
         sgt[now].sum=a[l];
         return;
     }
     Build_sgt(lch,l,smid);
     Build_sgt(rch,smid+,r);
     update(now);
 }
 long long Query_sgt(int now,int l,int r,int qx,int qy){
     if(l==qx&&r==qy)return sgt[now].sum;
     push_down(now,l,r);
     if(qy<=smid)return Query_sgt(lch,l,smid,qx,qy);
     if(qx>smid)return Query_sgt(rch,smid+,r,qx,qy);
     return Query_sgt(lch,l,smid,qx,smid)+Query_sgt(rch,smid+,r,smid+,qy);
 }
 void Region_add(int now,int l,int r,int x,int y,long long v){
     if(l==x&&r==y){
         set_lazy(now,l,r,v);
         return;
     }
     push_down(now,l,r);
     if(y<=smid)Region_add(lch,l,smid,x,y,v);
     else if(x>smid)Region_add(rch,smid+,r,x,y,v);
     else{
         Region_add(lch,l,smid,x,smid,v);
         Region_add(rch,smid+,r,smid+,y,v);
     }
     update(now);
 }
 int main(){
     scanf("%d%d",&N,&M);
     for(int i=;i<=N;i++)
         scanf("%lld",a+i);
     int root=;
     Build_sgt(root,,N);
     int op,x,y;
     long long k;
     for(int i=;i<=M;i++){
         scanf("%d",&op);
         switch(op){
             case :
                 scanf("%d%d%lld",&x,&y,&k);
                 Region_add(,,N,x,y,k);
                 break;
             case :
                 scanf("%d%d",&x,&y);
                 printf("%lld\n",Query_sgt(,,N,x,y));
                 break;
         }
     }
     return ;
 }