POJ3368(Frequent values)--线段树

题目在这里

3368

Accepted

7312K

1829MS

C++

6936B

题意为给你一组数据，再给定一组区间，问你这个区间内出现次数最多的元素的次数是多少。

我还记得这题是学校校赛基础的题目，当时懵懵懂懂的用分治交了6次TLE。知道了线段树之后才后悔每更早的认识她。

一段区间内的多次出现的数的次数，在线段树查询中有以下几种情况

1.次数最多的都集中在某一结点的左区间内

2.次数最多的都集中在某一结点的有区间内

3.次数最多的在左右两边都有，这时maxCount ==左右两边的maxCount之和

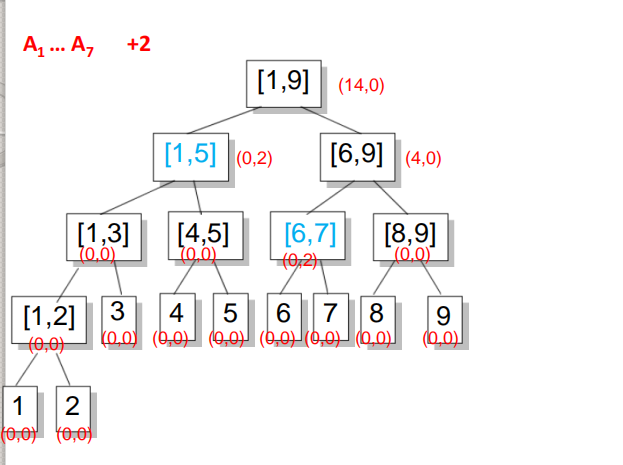
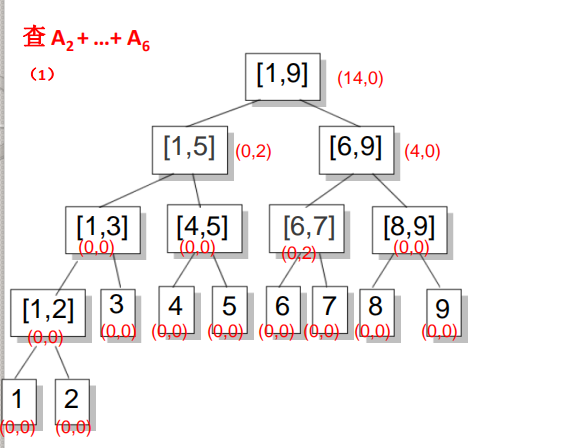
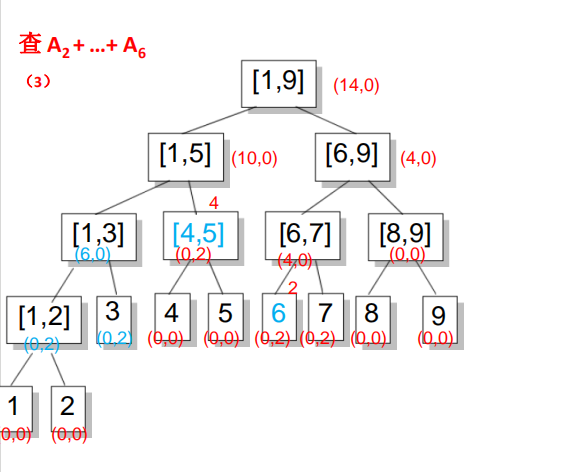
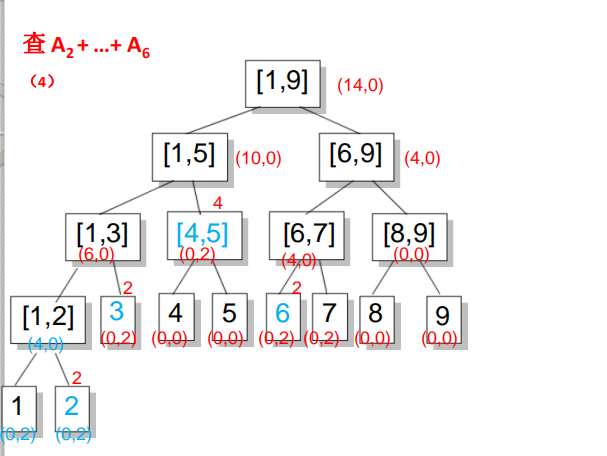
在增加时，如果要加的区间正好覆盖一个节点，则增加其节点的Inc值，不再往下走，否则要更新nSum(加上本次增量),再将增量往下传。这样更新的复杂度就是O(log(n))在查询时，如果待查区间不是正好覆盖一个节点，就将节点的Inc往下带，然后将Inc代表的所有增量累加到nSum上后将Inc清0，接下来再往下查询。

 /*************************************************************************
     > File Name: poj3368rmq.cpp
     > Author: YeGuoSheng
     > Description:
     > Created Time: 2019年07月11日 星期四 15时34分56秒
  ************************************************************************/

 #include<iostream>
 #include<stdio.h>
 #include<cstring>
 #include<cmath>
 #include<vector>
 #include<stack>
 #include<map>
 #include<set>
 #include<list>
 #include<queue>
 #include<string>
 #include<algorithm>
 #include<iomanip>
 using namespace std;

 template <typename T>
 struct node
 {
     int l;
     int r;//左右区间端点
     T value;
     T add;
     int lCount;//元素在左边的计数
     int rCount;//元素在右边的计数
     int maxCount;//总计出现的次数
     int Len()const;
     int Mid()const;
 };

 template <typename T>
 int node<T>::Mid()const
 {
     return (r  + l )/ ;
 }

 template<typename T>
 int node<T>::Len()const
 {
     return (r - l ) +;
 }

 template<typename T>
 class IntervalTree
 {
 protected:
     int n;
     node<T>*tree;
 public:
     IntervalTree(int n);
     ~IntervalTree();
     void BuildTree(int v,int l,int r);
     void Add(int v,int l,int r,T m);
     T Query(int v,int l,int r);
     void Insert(int v,int i,T value);
     void BuildCount(int v,int l,int r);
     int FindIndexInTree(int v,int y);//在数组下标为u的在树中的下标
 };

 template<typename T>
 IntervalTree<T>::IntervalTree(int n)
 {
     this->n = n;
     tree = new node<T>[*n];
 }

 template<typename T>
 IntervalTree<T>::~IntervalTree()
 {
     delete []tree;
 }

 template<typename T>
 void IntervalTree<T>::BuildTree(int v ,int l,int r)
 {
     tree[v].l =l;
     tree[v].r = r;
     tree[v].add = ;
     tree[v].value = ;
     if(l == r)//相等
     {
         tree[v].lCount =tree[v].rCount = tree[v].maxCount = ;
         return ;
     }
     int mid =(l + r) /;//二分
     BuildTree(v* +,l,mid);
     BuildTree(v*+,mid+,r);
     tree[v].value = tree[*v+].value + tree[*v+].value;
 }

 template<typename T>
 int IntervalTree<T>::FindIndexInTree(int v,int u)
 {
     if( tree[v].l == u && tree[v].r == u)
     {
         return v;
     }
     else
     {
         int mid = (tree[v].l + tree[v].r) / ;
         if(u <= mid)
         {
             FindIndexInTree(v * +,u);
         }
         else
         {
             FindIndexInTree(v * +,u);
         }
     }
 }

 template<typename T>
 void IntervalTree<T>::BuildCount(int v,int l ,int r)
 {
     tree[v].l = l;
     tree[v].r = r;
     if(l == r)
     {
         tree[v].lCount = tree[v].rCount =tree[v].maxCount = ;
         return ;
     }
     int mid  = (l + r )/ ;
     BuildCount(* v+ ,l,mid);
     BuildCount(*v +,mid+,r);
     int repeat = ;
     int leftIndex = FindIndexInTree(v,tree[*v+].r);
     int rightIndex = FindIndexInTree(v,tree[*v+].l);
     if(tree[leftIndex].value == tree[rightIndex].value)
     {
         repeat = tree[ * v +].rCount + tree[*v +].lCount;
     }
     else
     {
         repeat = ;
     }
     tree[v].maxCount = max( repeat,max( tree[*v+].maxCount, tree[*v+].maxCount) );
     tree[v].lCount = tree[*v+].lCount;
     if(tree[*v + ].lCount == mid - l +  && tree[leftIndex].value==tree[rightIndex].value)
     {
         tree[v].lCount += tree[*v +].lCount;
     }
     if(tree[*v + ].rCount == r- mid  && tree[rightIndex].value==tree[leftIndex].value)
     {
         tree[v].rCount += tree[*v +].rCount;
     }
 }
 template<typename T>
 void IntervalTree<T>::Add(int v,int l,int r,T m)//区间的更新操作
 {
     if(tree[v].l == l && tree[v].r == r)
     {
         tree[v].add +=m;
         return ;
     }
     tree[v].value += m * (r- l +);
     int mid = (tree[v].l  + tree[v].r) /;
     if( r<= mid)
     {
         Add(v * +,l,r,m);
     }
     else
     {
         if(l > mid)
         {
             Add(v * +,l,r,m);
         }
         else
         {
             Add(v * +,l,mid,m);
             Add(v*+,mid+,r,m);
         }

     }

 }
 template<typename T>
 T IntervalTree<T>::Query(int v,int l,int r)//对根结点为v，查询区间l 到 r
 {
     if(tree[v].l == l && tree[v].r == r)
     {
         return tree[v].value +(tree[v].r - tree[v].l +) * tree[v].add;
     }
     if(tree[v].add != )
     {
         tree[v].value += (tree[v].r - tree[v].l +) * tree[v].add;
         Add( v *  +,tree[v].l,tree[v].Mid(),tree[v].add);
         Add( v *  +,tree[v].Mid()+,tree[v].r,tree[v].add);
         tree[v].add = ;
     }
     int mid = tree[v].Mid();
     if( r <= mid)
     {
         return     Query(v  *  +,l,r);
     }
     else
     {
         if( l > mid)
         {
             return Query(v * + ,l ,r);
         }
         else
         {
             return Query(v * +,l,mid) + Query(v* +,mid+,r);
         }
     }
 }

 template<typename T>
 void IntervalTree<T>::Insert(int r,int i,T value)
 {
     if(tree[r].l == i && tree[r].r == i)
     {
         tree[r].value= value;
         return ;
     }
     tree[r].value += value;
     if(i <= tree[r].Mid())
     {
         Insert(*r+,i,value);
     }
     else
     {
         Insert( * r+ ,i,value);
     }
 }

 int main()
 {
     int n = ;
     while(cin>>n && n > )
     {
         IntervalTree<int> it(n);
         it.BuildTree(,,n-);
         int q = ;
         scanf("%d",&q);
         for(int i = ; i< n;i++)
         {
             int num = ;
             scanf("%d",&num);
             it.Insert(,i,num);
         }
         it.BuildCount(,,n-);
         for(int i = ;i < q;i++)
         {
             int x,y;
             cin>>x>>y;
             cout<<it.Query(,x-,y-)<<endl;
         }
     }
     return ;
 }