李宏毅 线性回归预测PM2.5

作业说明

　　给定训练集train.csv，要求根据前9个小时的空气监测情况预测第10个小时的PM2.5含量。

训练集介绍：

　　(1)：CSV文件，包含台湾丰原地区240天的气象观测资料(取每个月前20天的数据做训练集，12月X20天=240天，每月后10天数据用于测试，对学生不可见);

　　(2)：每天的监测时间点为0时，1时......到23时，共24个时间节点;

　　(3)：每天的检测指标包括CO、NO、PM2.5、PM10等气体浓度，是否降雨、刮风等气象信息，共计18项；

(4):数据集https://github.com/datawhalechina/leeml-notes/blob/master/docs/Homework/HW_1/Dataset

数据处理

【下文中提到的“数据帧”并非指pandas库中的数据结构DataFrame,而是指一个二维的数据包】

根据作业要求可知，需要用到连续9个时间点的气象观测数据，来预测第10个时间点的PM2.5含量。针对每一天来说，其包含的信息维度为(18,24)(18项指标，24个时间节点)。可以将0到8时的数据截

取出来，形成一个维度为(18,9)的数据帧，作为训练数据，将9时的PM2.5含量取出来，作为该训练数据对应的label；同理可取1到9时的数据作为训练用的数据帧，10时的PM2.5含量作为label......以此

分割，可将每天的信息分割为15个shape为(18,9)的数据帧和与之对应的15个label。

好像是说用excel是打不开数据文件的  然后亲测是可以打开的，下面是数据标注分析。

# 数据读取与预处理
train_data = pd.read_csv("leeml-notes-docs-Homework-HW_1./Dataset/train.csv")
train_data.drop(['Date', 'stations'], axis=1, inplace=True)
column = train_data['observation'].unique()
# print(column)
new_train_data = pd.DataFrame(np.zeros([24*240, 18]), columns=column)

for i in column:
    train_data1 = train_data[train_data['observation'] == i]
    # Be careful with the inplace, as it destroys any data that is dropped!
    train_data1.drop(['observation'], axis=1, inplace=True)
    train_data1 = np.array(train_data1)
    train_data1[train_data1 == 'NR'] = ''
    train_data1 = train_data1.astype('float')
    train_data1 = train_data1.reshape(1, 5760)
    train_data1 = train_data1.T
    new_train_data[i] = train_data1

label = np.array(new_train_data['PM2.5'][9:], dtype='float32')

探索性数据分析EDA 。最简但粗暴的方式就是根据HeatMap热力图分析各个指标之间的关联性。

【探索性数据分析（Exploratory Data Analysis，简称EDA）】

摘抄网上的一个中文解释，是指对已有的数据（特别是调查或观察得来的原始数据）在尽量少的先验假定下进行探索，通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。特别是当我们对面对大数据时代到来的时候，各种杂乱的“脏数据”，往往不知所措，不知道从哪里开始了解目前拿到手上的数据时候，探索性数据分析就非常有效。探索性数据分析是上世纪六十年代提出，其方法有美国统计学家John Tukey提出的。

附上：Howard Seltman 探索数据分析的英语文档http://www.stat.cmu.edu/~hseltman/309/Book/chapter4.pdf

【热力图 heatmap】

seaborn.heatmap(data, vmin=None, vmax=None,cmap=None, center=None, robust=False, annot=None, fmt=’.2g’, annot_kws=None,linewidths=0, linecolor=’white’, cbar=True, cbar_kws=None, cbar_ax=None,square=False, xticklabels=’auto’, yticklabels=’auto’, mask=None, ax=None,**kwargs)

参数共有20个，其中除了data的参数以外，其他的都有默认值。利用热力图可以看数据表中多个特征凉凉的相似度。

（1）热力图输入数据参数

data:data是热力图输入的数据参数，矩阵数据集，可以是numpy的数组（array），也可以是pandas的DataFrame。如果是DataFrame，则df的index/column信息会分别对应到heatmap的columns和rows，即pt.index是热力图的行标，pt.columns是热力图的列标。

（2）热力图矩阵块颜色参数:

vmax,vmin:分别是热力图的颜色取值最大和最小范围，默认是根据data数据表里的取值确定

cmap:从数字到色彩空间的映射，取值是matplotlib包里的colormap名称或颜色对象，或者表示颜色的列表；改参数默认值：根据center参数设定

center:数据表取值有差异时，设置热力图的色彩中心对齐值；通过设置center值，可以调整生成的图像颜色的整体深浅；设置center数据时，如果有数据溢出，则手动设置的vmax、vmin会自动改变

robust:默认取值False；如果是False，且没设定vmin和vmax的值，热力图的颜色映射范围根据具有鲁棒性的分位数设定，而不是用极值设定

（3）热力图矩阵块注释参数:

annot(annotate的缩写):默认取值False；如果是True，在热力图每个方格写入数据；如果是矩阵，在热力图每个方格写入该矩阵对应位置数据

fmt:字符串格式代码，矩阵上标识数字的数据格式，比如保留小数点后几位数字

annot_kws:默认取值False；如果是True，设置热力图矩阵上数字的大小颜色字体，matplotlib包text类下的字体设置

（4）热力图矩阵块之间间隔及间隔线参数：

linewidths:定义热力图里“表示两两特征关系的矩阵小块”之间的间隔大小

linecolor:切分热力图上每个矩阵小块的线的颜色，默认值是’white’

（5）热力图颜色刻度条参数：

cbar:是否在热力图侧边绘制颜色刻度条，默认值是True

cbar_kws:热力图侧边绘制颜色刻度条时，相关字体设置，默认值是None

cbar_ax:热力图侧边绘制颜色刻度条时，刻度条位置设置，默认值是None

（6）square:设置热力图矩阵小块形状，默认值是False

预测pm2.5所使用的热力图分析   //  代码如下

f, ax = plt.subplots(figsize=(9, 6))
sns.heatmap(new_train_data.corr(), fmt="d", linewidths=0.5, ax=ax)
plt.show()

模型选择线性回归模型   //  代码如下

# a.数据归一化
# 使用前九个小时的 PM2.5 来预测第十个小时的 PM2.5，使用线性回归模型
PM = new_train_data['PM2.5']
PM_mean = int(PM.mean())
PM_theta = int(PM.var()**0.5)
PM = (PM - PM_mean) / PM_theta
w = np.random.rand(1, 10)
theta = 0.1
m = len(label)
for i in range(100):
    loss = 0
    i += 1
    gradient = 0
    for j in range(m):
        x = np.array(PM[j : j + 9])
        x = np.insert(x, 0, 1)
        error = label[j] - np.matmul(w, x)
        loss += error**2
        gradient += error * x

    loss = loss/(2*m)
    print(loss)
    w = w+theta*gradient/m

源代码：

#pm2.5 prediction
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 数据读取与预处理
train_data = pd.read_csv("leeml-notes-docs-Homework-HW_1./Dataset/train.csv")
train_data.drop(['Date', 'stations'], axis=1, inplace=True)
column = train_data['observation'].unique()
# print(column)
new_train_data = pd.DataFrame(np.zeros([24*240, 18]), columns=column)

for i in column:
    train_data1 = train_data[train_data['observation'] == i]
    # Be careful with the inplace, as it destroys any data that is dropped!
    train_data1.drop(['observation'], axis=1, inplace=True)
    train_data1 = np.array(train_data1)
    train_data1[train_data1 == 'NR'] = ''
    train_data1 = train_data1.astype('float')
    train_data1 = train_data1.reshape(1, 5760)
    train_data1 = train_data1.T
    new_train_data[i] = train_data1

label = np.array(new_train_data['PM2.5'][9:], dtype='float32')

# 探索性数据分析 EDA
# 最简单粗暴的方式就是根据 HeatMap 热力图分析各个指标之间的关联性
f, ax = plt.subplots(figsize=(9, 6))
sns.heatmap(new_train_data.corr(), fmt="d", linewidths=0.5, ax=ax)
plt.show()

# 模型选择
# a.数据归一化
# 使用前九个小时的 PM2.5 来预测第十个小时的 PM2.5，使用线性回归模型
PM = new_train_data['PM2.5']
PM_mean = int(PM.mean())
PM_theta = int(PM.var()**0.5)
PM = (PM - PM_mean) / PM_theta
w = np.random.rand(1, 10)
theta = 0.1
m = len(label)
for i in range(100):
    loss = 0
    i += 1
    gradient = 0
    for j in range(m):
        x = np.array(PM[j : j + 9])
        x = np.insert(x, 0, 1)
        error = label[j] - np.matmul(w, x)
        loss += error**2
        gradient += error * x

    loss = loss/(2*m)
    print(loss)
    w = w+theta*gradient/m

热力图展示：

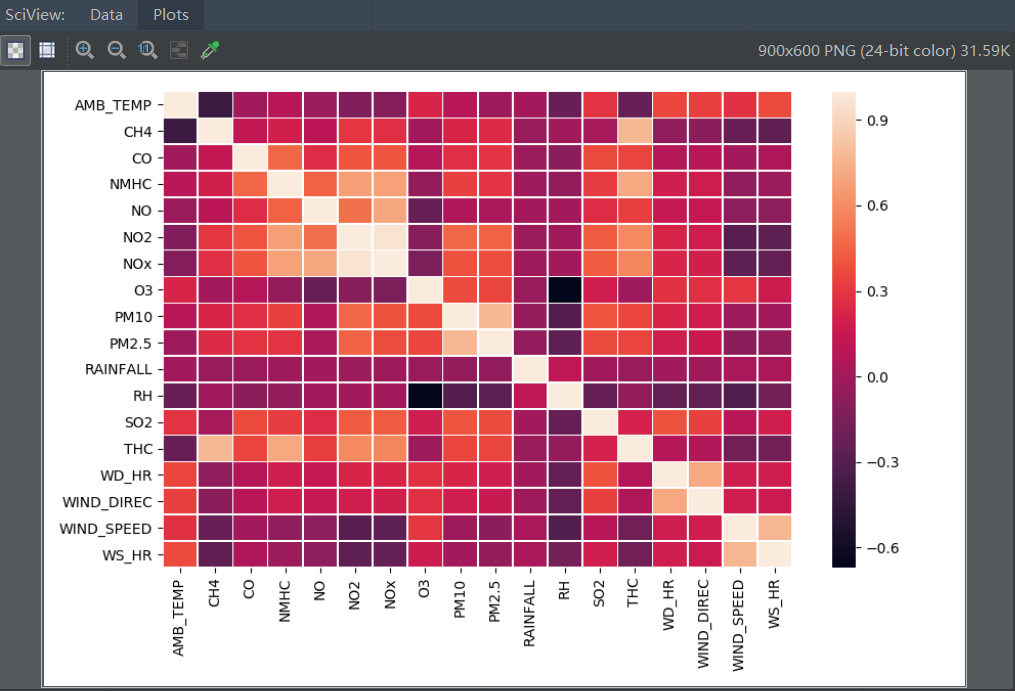
通过热力图分析，可以直接看出来，与PM2.5相关性较高的指标有PM10、NO2、SO2、NOX、O3、THC。

打印损失函数

[292.68906502]
[223.74087258]
[185.8738045]
[156.51287584]
[132.85031907]
[113.69306898]
[98.15763341]
[85.54014962]
[75.27576792]
[66.910614]
[60.07971]
[54.48935648]
[49.90304759]
[46.13020108]
[43.01713361]
[40.43982902]
[38.29813911]
[36.51113006]
[35.01334584]
[33.75180584]
[32.68359109]
[31.77390253]
[30.99449797]
[30.32243337]
[29.73904841]
[29.22914866]
[28.78034581]
[28.38252508]
[28.0274152]
[27.70824084]
......