【AGC002 E】Candy Piles

本来实在写不动这题 sol 了，但一想这是个经典的模型转化问题，于是就写了（.jpg）

题意

　　有一个序列 \(a_i\)。

　　两人轮流操作，每次操作为二选一：

　　　　1. 把最大的 \(a_i\) 减成 \(0\)

　　　　2. 把所有非 \(0\) 的 \(a_i\) 减去 \(1\)

　　若一个人操作后，所有 \(a_i\) 都是 \(0\)，这个人就输了。

　　两人都采用轮流策略，问谁能赢。

　　\(n\le 10^5\)

　　\(a_i\le 10^9\)

题解

　　智商模型转化：把所有 \(a_i\) 从大到小排序，画一个柱状图，第 \(i\) 个柱子的高度为 \(a_i\)。每个人可以删去最左边一列或最下边一行，求谁操作后删光整个柱状图。

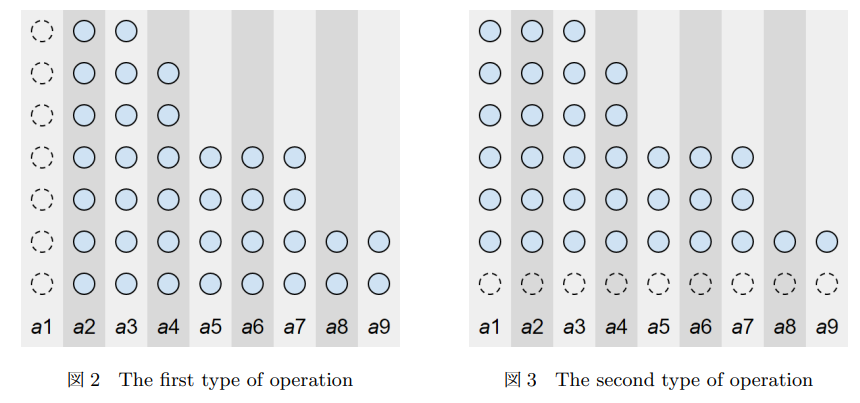
　　我们发现每次操作后，图的左下角一定会移动，并且一个左下角对应一种游戏局面。

　　所以，这个模型还可以转化：从左下角出发，两人轮流向上或向右走一个单位，走到边界的人输。

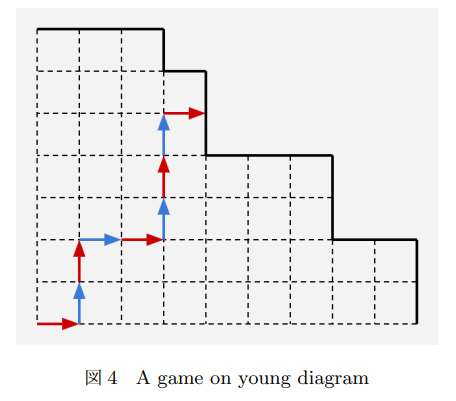
　　这是个很简单的博弈论 \(\text{dp}\)，每个点对应一个操作者的必胜态 / 必败态。将操作者的胜败状态记在该操作到达的点上，则边界上全是必败态，\((1,1)\) 是后手的胜败状态（因为先手从这里出发到邻点，胜败状态在两个邻点上，通过那两个点的胜败状态算出的胜败状态 相当于后手在游戏开始时的胜败状态）。

　　直接 \(O(n\times a_i)\) \(\text{dp}\) 即可求出每个点是必胜态还是必败态。

　　但这样显然会 T，我们考虑优化。

　　随便画一个图，手玩出每个点的胜败状态（红圈表示必败态，蓝叉表示必胜态）

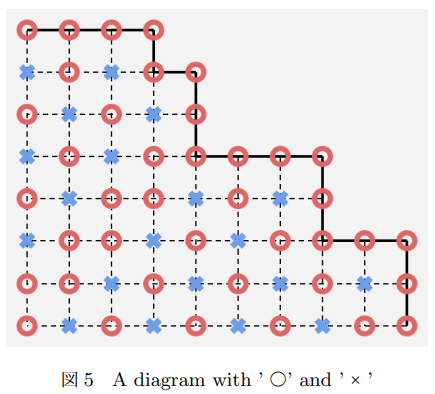
　　不难发现左下-右上对角线上的状态都是一样的！如何证明？

　　假如 \((x,y)\) 是 \(1\)，\((x-1,y-1)\) 不可能是 \(0\)。这里用反证法，举一个例子：

　　0 ?

　　1 1 ?

　　0 1 0

　　注意到 \(0\) 的后继全都是 \(1\)，\(1\) 的后继一定有 \(0\)。

　　可以画出这样的图。

　　发现两个 ? 处至少有一个 \(0\)（\(1\) 的后继一定有 \(0\)），但两个 ? 处都必须是 \(1\)（\(0\) 的后继全部是 \(1\)），因此矛盾。

　　以上图为例，我们就只需要算 \((4,4)\) 的胜败状态了！

　　这个位置怎么算呢？

　　它的上边、右边所有点都贴着边界，状态为胜、败轮流交替。于是可以从

　　以上图为例，从 \((4,7)\) 往下根据奇偶性推出 \((4,5)\) 的状态，从 \((8,4)\) 往左推出 \((5,4)\) 的状态，然后根据 \((4,5)\) 和 \((5,4)\) 的状态就可以推出 \((4,4)\longrightarrow (1,1)\) 的状态了。

　　复杂度 \(O(n)\)。

#include<bits/stdc++.h>
using namespace std;
int a[100005];
int main(){
    int n,i;
	scanf("%d",&n);
    for(i=1; i<=n; ++i) scanf("%d",&a[i]);
    sort(a+1, a+n+1, greater<int>());
    for(i=1; i<=n; ++i){
        if(i<=a[i] && a[i+1]<i+1){
            int j=0;
            while(a[j+i+1]==i) j++;
            if((a[i]-i)%2==0 && j%2==0) puts("Second");
            else puts("First");
            return 0;
        }
    }
}