【零基础】神经网络优化之L1、L2

一、序言

　　前面的文章中，我们逐步从单神经元、浅层网络到深层网络，并且大概搞懂了“向前传播”和“反向传播”的原理，比较而言深层网络做“手写数字”识别已经游刃有余了，但神经网络还存在很多问题，比如最常见的两个问题：“过拟合”和“欠拟合”，下图中从左到右依次是“欠拟合”、“刚刚好”、“过拟合”。

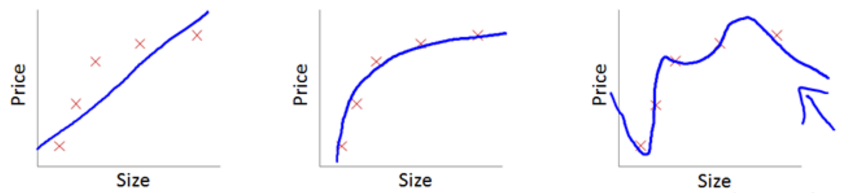
　　简单点说，欠拟合是我们学习到的w没能很好地“满足”训练数据的特征，一般是因为训练数据太少、训练次数不够、神经网络太简单等问题，优化地方法也比较容易，有针对性地增加训练数据、训练次数或使用更复杂的网络即可。过拟合则刚好相反，我们学习到的w与训练数据太契合了，以至于在实际场景中反而表现很差。本文就简单介绍下过拟合常见优化方法中的一种“L2”，之所以叫L2是因为它前面还有L0和L1。

二、正则化

　　无论是L0、L1、L2，本质上都是希望实现w的正则化，那何为正则化？严格定义如下：

　　　　就是给平面不可约代数曲线以某种形式的全纯参数表示。

　　用人话说就是：

　　　　对某一问题加以先验的限制或约束以达到某种特定目的的一种手段或操作。

　　还是不好理解的话，可以代入到当前应用场景里来理解：

　　　　所谓过拟合就是训练得到的w导致求解曲线过于契合训练数据，正则化就是将“过于契合”变为不那么契合，方法是让求解曲线变得更加“平滑”：

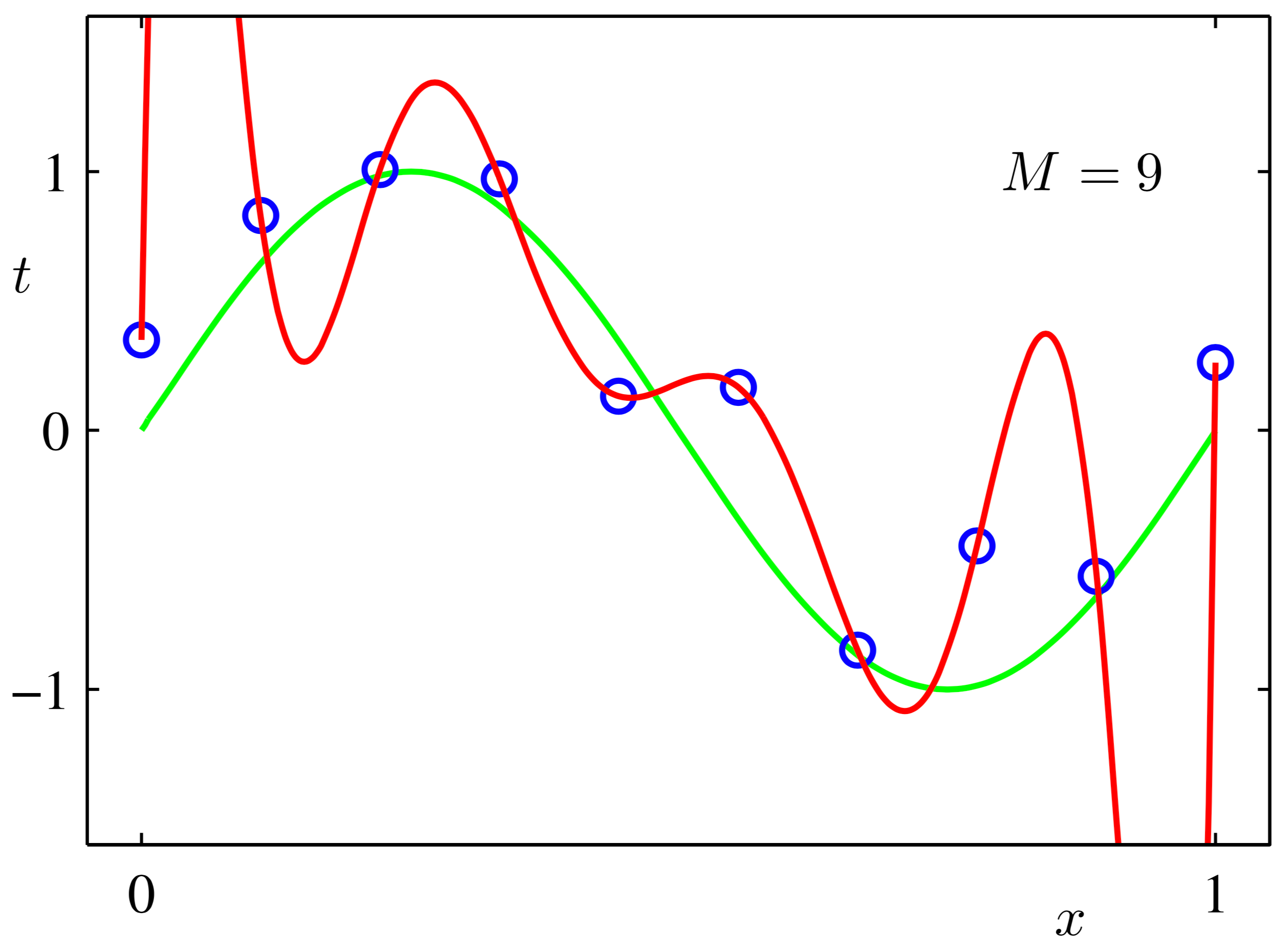
　　　　上图中，红色曲线就是过于契合训练数据（过拟合），而绿色曲线就是正则化后的结果（平滑）。

三、L0

　　L0是一种处理方法，简单来说：

　　　　L0 范数指向量中非 0 元素的个数。如果用 L0 范数来规则化一个参数矩阵 W 的话，就是希望 W 的大部分元素是 0，即让参数 W 是稀疏的。

　　不是很好理解，我们可以代入实际问题中。假设现在有如下的W

　　W = w1,w2,w3,w4,w5

　　对W进行L0正则化，就是在求dW时，先看看W中有那些元素是“非0”的，我们一般认为输入中非0的元素是相对“重要”的。现在假设w1、w2为非0数，w3、w4、w5为0，则W中非0数为2个。

　　W = w1, w2, 0, 0, 0

　　L0 = 2

　　进行相应dw计算时，先看一下dw有多少位是非0的，假设dw1、dw2、dw3为非0数，dw4、dw5为0。

　　dw = dw1, dw2, dw3, 0, 0

　　我们发现dw非0的数多于L0，那么我们就将dw中的某一个非0数置为0（比如dw3）。dw就变为：

　　dw = dw1, dw2, 0, 0, 0

　　如此一来，在做W更新时，部分元素是不更新的（减去的是0），仅更新最多L0个元素。考虑一种理想情况，比如通过L0我们刚好将曲线中一些不重要信息排除掉，那是不是就实现了曲线的“平滑”？其次实践中我们会发现，优化W时其内部元素总是有冲动趋向于极大或极小（即重要的信号越来越重要，不重要的信号越来越不重要），通过L0我们可以延缓这一趋势。

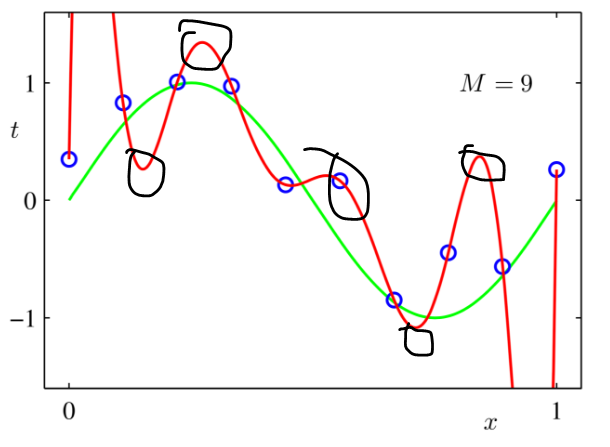
　　但问题是那些信号是不重要的，那些才是重要的？L0很难去判定，所以L0在实际使用时会有一点作用，但效果好坏全凭运气。

四、L1

　　L1相对就比较直接了，它直接在损失函数后加上一个小尾巴：

　　L1 = λ*|W|

　　其中λ是一个超参（也就是可以人为设置的），用来调节L1影响的幅度。

　　先回忆一下损失函数的样子

　   其中Label是训练数据中标注的正确答案，Y是传播函数预测的结果，Y = WX+b

　　加上L1的损失函数

　　为了求Δw，我们用新的损失函数对w求导

　　上式中前半截(Label-Y)^2对w求导在之前“看懂神经网络中的反向传播”已经写过就直接拿来用了，后半截这个w绝对值对w的求导很多地方写的不清不楚让人痛苦，翻了翻高中课本方恍然大悟：

　　对绝对值求导的结果就是将|W|分为了三段，大于0、等于0、小于0，大于0的部分求导后为1、小于0的部分求导后为-1、等于0的部分不能求导就让结果直接为0吧。所以：

　　Δw = 2*(Label - Y)*x + λ*f(w)

　　其中f(w)在w大于0时为1，小于0时为-1，等于0时为0.

　　由于Δw的结果与W相关，所以L1最后实现的效果就是将W中“正值减小”（多减了一部分正的λ）、“负值增大”（多减了一部分负的λ），也即是使W更加“平滑”。

 五、L2

　　L1让人看起来已经感觉很棒棒了，但实际使用时还是感觉不够劲爆所以又有了L2。L2较L1就只做了一点微小的改变：

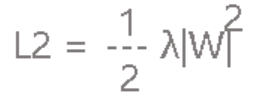
　　是的，就只是将w变为w的平方而已，乘以1/2只是为了后面计算方便。

　　我们一样将L2作为小尾巴放到损失函数的屁股后面：

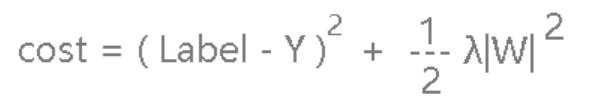
　　这里求导就很简单了

　　Δw = 2*(Label - Y)*x + λ*W

　　L2很简洁，意义与L1差不多都是在更新w时进行一定程度的衰减（w中的负值和正值都更趋向于0）。较L1不同的是L2是按W的一定比例进行衰减，而L1只是简单地减去λ。具体啥好处说不上来，反正大家都用L2

六、总结

　　公式推导这里花了不少时间，真的推导出来后我发现，当年发明L1、L2的人肯定是先找到了Δw减去这么个值效果很棒，然后再回头去推导cost的计算公式，要不然咋这么巧呢？

　　这里只做了公式的推导，具体代码就不放出来了（因为求解的问题太简单，以至于加上L1、L2后没啥优化效果），以后把所有优化整全了再发个完整的代码包。

请关注公众号“零基础爱学习”一起AI学习。