Leetcode之广度优先搜索（BFS）专题-133. 克隆图（Clone Graph）

Leetcode之广度优先搜索（BFS）专题-133. 克隆图（Clone Graph）

BFS入门详解：Leetcode之广度优先搜索（BFS）专题-429. N叉树的层序遍历（N-ary Tree Level Order Traversal）

---

给定无向连通图中一个节点的引用，返回该图的深拷贝（克隆）。图中的每个节点都包含它的值 val（Int） 和其邻居的列表（list[Node]）。

示例：

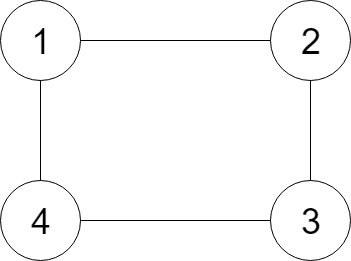
输入：
{"$id":"1","neighbors":[{"$id":"2","neighbors":[{"$ref":"1"},{"$id":"3","neighbors":[{"$ref":"2"},{"$id":"4","neighbors":[{"$ref":"3"},{"$ref":"1"}],"val":4}],"val":3}],"val":2},{"$ref":"4"}],"val":1}

解释：
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

提示：

1. 节点数介于 1 到 100 之间。
2. 无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
3. 由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
4. 必须将给定节点的拷贝作为对克隆图的引用返回。

---

给定一个图，复制这个图，返回拷贝。

思路如下：

1、new一个map，Key用于存储旧的节点，Value用于存储新的节点

2、把node开始加入queue，开始BFS

3、BFS

• 取出节点temp，遍历他的所有邻居n
• 查map，看是否邻居n已拷贝
• 如果邻居n未拷贝，则拷贝完，把b节点加入queue
• 把temp的邻居列表List取出，把上述一步拷贝成功的邻居节点加入到List里
• 返回第三步，queue为空则跳出

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;

    public Node() {}

    public Node(int _val,List<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/
class Solution {
    public Node cloneGraph(Node node) {
        if(node==null) return node;
        Queue<Node> queue = new LinkedList<>();
        Map<Node,Node> map = new HashMap<>();
        Node ans = new Node(node.val,new ArrayList<>());
        map.put(node,ans);

        queue.offer(node);
        while(!queue.isEmpty()){
            Node temp = queue.poll();
            for(Node nb:temp.neighbors){
                if(!map.containsKey(nb)){
                    map.put(nb,new Node(nb.val,new ArrayList<>()));
                    queue.offer(nb);
                }
                map.get(temp).neighbors.add(map.get(nb));
            }
        }

        return ans;
    }
}