SIGAI机器学习第十七集 线性模型1

讲授logistic回归的基本思想，预测算法，训练算法，softmax回归，线性支持向量机，实际应用

大纲：

再论线性模型
logistic回归的基本思想
预测函数
训练目标函数
梯度下降法求解
另一种版本的对数似然函数
L2正则化logistic回归
L1正则化logistic回归
liblinear简介
实验环节
softmax回归
实际应用

线性模型分两类，一类是逻辑斯蒂回归，另一种是线性的SVM。

liblinear和libSVM是兄弟库，同一波人开发的。

logistic本来是二分类器，扩展一下成为softmax回归完成多分类问题，softmax在深度学习中是非常有用的，对于多分类问题深度神经网络最后一层往往是softmax。

再论线性模型：

线性模型分为分类、回归两大类算法。

线性回归（有岭回归和LASSO回归）都是凸优化问题。

对于分类也有几个分支，最基本的线性分类器sgn(w^Tx+b)感知器模型，对它进行扩展就是SVM，感知器是对样本尽可能的分正确而SVM在样本尽可能分正确的基础上最大化分类间隔，感知器另外一个分支是logistic回归。

大部分算法都是非线性的，非线性算法准确率更高，现实中数据data多是非线性的，但线性算法也有它的优点：

①实现简单，计算效率高。预测时只需两个向量内积加一个标量再做一个判断就行了sgn(w^Tx+b)，对于回归问题只需内积加标量无需判断w^Tx+b，因此计算效率非常高。

②对大规模分类问题与回归问题是很好的选择。在实际应用中，特征向量x的维数会非常高，属于Rⁿ空间，n可能有上亿，如搜索引擎方面，而且样本数会非常庞大上亿规模，这时用非线性模型计算效率会非常差，根本没法在实际应用中使用它，根本算不过来，因此在大规模的分类或者回归问题中，线性模型虽然很简单但还是一个比较好的选择，就像决策树一样虽然很简单但是效率非常高。

logistic回归的基本思想：

1/(1+e^-x)，sigmoid函数还有一个名字是logistic函数，定义域是(-∞, +∞)，单调增，值域是(0, 1)。

对于二分类问题，直接估计样本属于每个类的概率，可以用logistic函数，为什么选用logistic函数？

值域为(0, 1)，刚好符合概率的要求，而且单调增，可以用作分布函数，也可以用于表示离散型随机变量的概率值。

但是logistic函数输入是一元变量，但是样本一般是多维向量，怎么办呢？可以z=w0+w1x+...wnxn，将z带入logistic预测函数直接输出样本属于正样本的概率。

将x扩展得到，这样任给一个样本x，就可以输出它属于正负样本的概率，就可以拿这个概率值来分类。

核心就是拿特征向量x用权重向量映射加权求和，再用logistic函数映射一下得到0到1之间的概率值，这个概率就是样本属于正样本的概率值。

预测函数：

前边知道logistic回归的映射函数为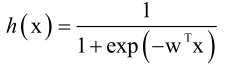，那么分类规则为h(x)>0.5，如果成立判定为1，否则判定为0。

logistic回归虽然名字有回归，但是他是一个分类算法，而且是二分类算法，不是回归算法。

logistic回归它的名字来历是对数几率回归，核心的概念就是对数似然比：

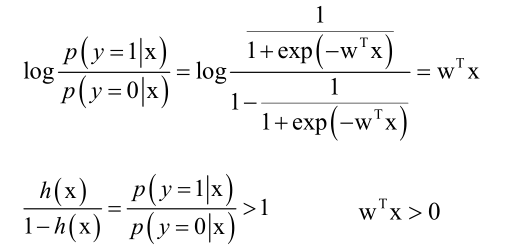
可知对数似然比大于0属于正样本。

logistic回归虽然预测函数中带有非线性的映射函数，但它本质上还是一个线性模型，因为它是一对一的单调的映射，神经网络的每个神经元也是这样的一个映射为什么神经网络是非线性模型呢？那是因为它是由多个神经元构成的，而且是多层复合的，所以它是一个非线性的模型。

对样本用logistic回归对两类问题进行分类拟合出一条曲线，这是不对的，因为它本质上是线性模型，无论样本多么复杂是否线性可分，到最后拟合出来的分类的边界都是一条直线。所以在非线性可分的问题上logistic回归算法的效果不如SVM、神经网络等算法效果好，存在错分样本。

训练目标函数：

前面提到logistic的映射函数是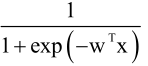，但是w是怎么得到的呢？是通过训练得到的。

假设有一批样本，那么为它构造一个目标函数，前边的算法都是最小化损失函数来实现的（如神经网络的训练目标是让预测输出值和真实样本的标签值y尽可能的接近，定义了一个叫欧氏距离的损失函数；对于SVM，它要最大化分类间隔；对于贝叶斯分类器，要确定概率分布的参数，对于离散型要把概率分布表算出来，对于连续型如果服从正态分布的话要把它的均值和方差或协方差矩阵给估计出来），这里logistic用的是最大似然估计MLE，为什么不直接用欧氏距离这样的损失函数来估计它呢？是因为logistic的预测函数的值是落在0到1之间的，而样本的标签值要么是0要么是1，直接相减的话效果是非常差的，因此采用最大似然估计。而且现在是来估计概率里边的一个参数，最大似然估计会好一些。最大似然估计的核心是让这组样本发生的概率最大化，即要最大化我们的最大似然函数。

样本属于每一类的概率可以统一写成下面的形式：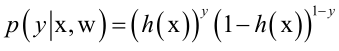

构造似然函数：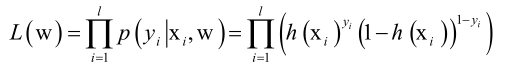

对数似然函数：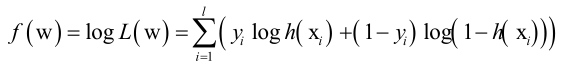

似然函数是每个样本的概率的乘积，为什么要构造对数似然函数呢？因为在求极值的时候要求导，似然函数求导不好求，取对数变成加法求导好求，而且对数函数是单调递增的，这里log函数的底数取e，最大化似然函数就等价于最大化对数似然函数。

即最终优化目标是：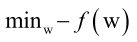

下边来证明这个优化问题是凸优化问题。

logistic函数的导数很优美：

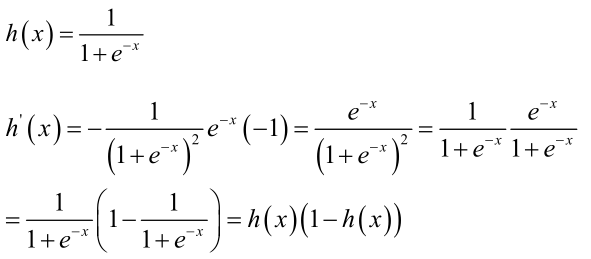
怎么证明logistic的最大似然估计是凸优化问题？分两种情况讨论，先对单个样本的损失函数，如果它是凸函数，那所有样本的损失函数加起来也是凸函数（凸函数的非负线性组合还是凸函数）。证明单个样本的函数是凸函数，分两种情况讨论：

如果是负样本，yi=0，即优化函数为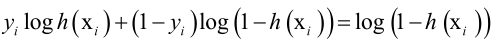

然后对w求导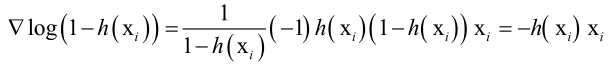

对w的Hession矩阵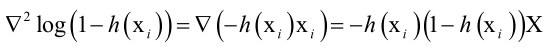

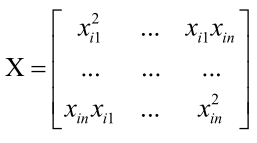
则负样本的目标函数的Hessian矩阵为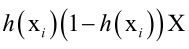，因为目标函数是-f(w)，所以加一个负号。

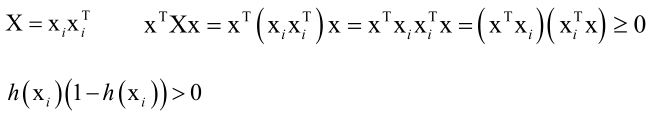
所以对于负样本的目标函数是凸函数。

如果是正样本，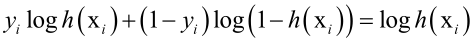

Hessian矩阵为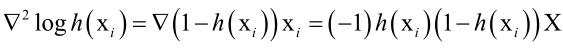

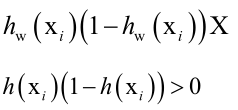
所以对于正样本的目标函数也是凸函数。

总之，对单个样本的目标函数都是凸函数。所以对于整个的损失函数目标函数也是凸函数，因此logistic回归训练的时候如果用最大似然估计MLE的话，最后求解的问题是一个凸优化问题，这是一个非常好的性质，跟SVM一样，一定能找到全局极小值点，这也是它受欢迎的原因之一。SVM、logstic回归、岭回归、标准的线性回归、LASSO回归等等这些都属于凸优化问题，而神经网络它就不是一个凸优化问题。

梯度下降法求解：

已经证明了logistic回归训练的时候优化的函数是一个凸函数，那可以最简单的采用梯度下降法来求解。

计算整个目标函数的梯度值：

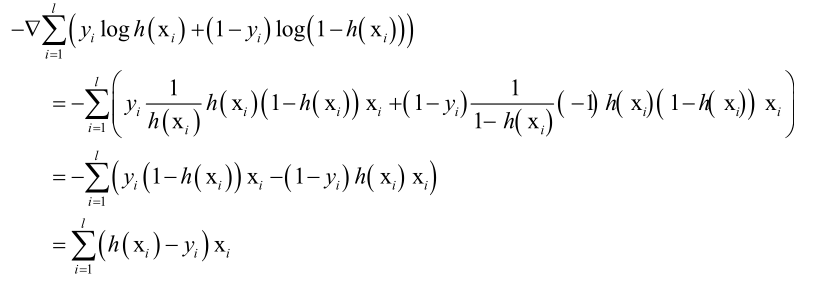
得到梯度值，带入梯度下降法公式中直接更新，梯度下降法的更新公式为：

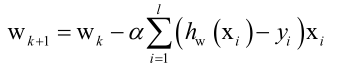
logistic一般用于大规模样本的分类问题里边，所以如果样本数量大，不能梯度下降法迭代时拿所有样本进行迭代，对于凸优化问题SGD会收敛的非常好的，也可以采用二阶优化技术，牛顿法，拟牛顿法，都可以保证收敛到全局最优解上。再用梯度下降法迭代的时候，w初始值设置为多少合适的，最简单的设置为全0或1都是可以的，更复杂的随机值作为初始值都是可以的。

另一种版本的对数似然函数：

前边对于定义的模型样本的标签值是0和1，分别对应于负样本和正样本，对于二分类问题还有另一种表示法，正负样本标签值为+1和-1，和前边SVM等算法是一样的，这样定义前边logistic的目标函数可以写的更简洁一些。即一个公式就统一掉了：

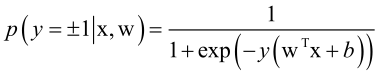
即：

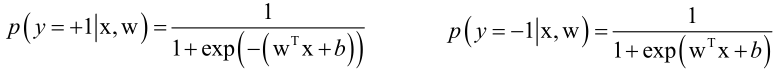，此时p(+1)=1-p(-1)。

则对数似然函数：

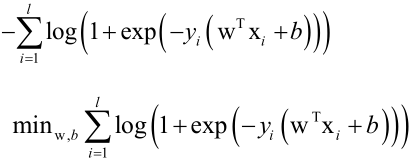
损失函数：

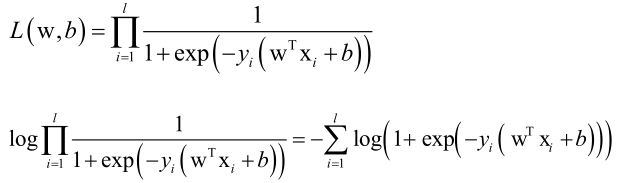
将w、x扩充，(w,b)-->w、(x,1)-->x，目标函数为：

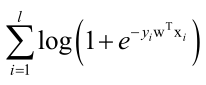
L2正则化logistic回归：

和其他机器学习算法一样，logistic回归同样会面临过拟合的情况，因此可以为它加上一个正则化项，原先加上正则化项的函数是L+λ1/2w^Tw，但为了好看，这里变形之后的目标函数为：

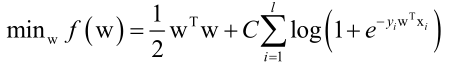
原本是求L的最小值，为了使模型更加光滑，要对复杂的模型进行惩罚，即让|w|更加的小接近于0，因此加上L2的正则化项。

可以证明对于加上L2正则化项的问题同样是一个凸优化问题：

1/2w^Tw的Hession矩阵是I，只需证明第二项是凸优化函数。

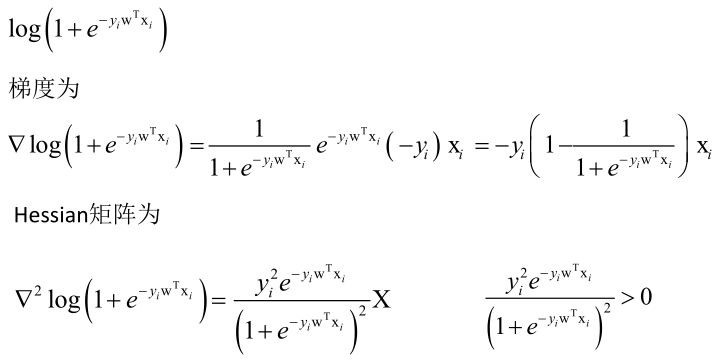
第二项的Hession矩阵正定，因此是带有L2正则化项的优化问题是凸优化问题，可以用梯度下降法或者牛顿法求解，由于是凸优化问题，一定能收敛到最优解，初始值的设定和前边一样，可以初始化为0、1都是可以的。

L1正则化logistic回归：

上边是加上L2正则化项的logistic回归，同样可以加上L1正则化项：

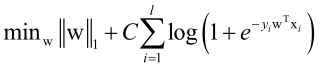
其中||w||=|w₁|+|w₂|+...，显然是凸函数，所以是凸优化问题，可以采用梯度下降法，牛顿法，坐标下降法求解都可以，就看哪一个快一些了。

liblinear简介：

上边讲了两种版本的logistic回归（0和1，+1和-1），都证明了他们是凸优化问题。

liblinear和libsvm是同一拨人编写的，由台湾大学林智仁教授与他的学生开发，风格也非常类似，是用c++写的、跨平台，依赖于一个简单的线性代数的库，也可以用其他的语言来调用。

他和libsvm不一样，它是适合用于大规模分类问题的求解，libsvm虽然也做了一些性能上的优化，但是libsvm主要支持非线性核的支持向量机，因此它对于真正的大规模的问题处理起来还是很慢的。如果要做大规模的分类，比如用logistic回归、线性SVM做算法的话，liblinear是一个非常好的选择，liblinear支持各种形式的logistic回归，以及线性SVM。liblinear接受的数据格式与libsvm相同。

同样他也带有自己的训练程序和预测程序，与libsvm类似：

实验环节：

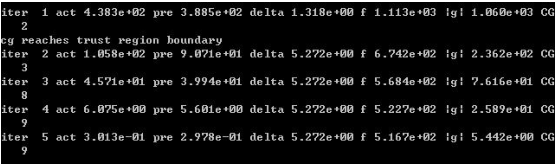
train -s 0 a1a a1a_model，其中a1a是从官网下载的训练文件的名称，训练过程：

训练之后，a1a_model文件中的一部分内容：

solver_type L2R_LR（求解器类型，L2正则化的逻辑斯蒂回归LR）
nr_class 2（分类数，因为liblinear不仅支持logistic回归，还支持线性svm，线性svm支持多分类，而logistic仅支持二分类）
label 1 -1（类别标签值）
nr_feature 119（样本特征向量的维数）
bias -1（偏置项的标志量，不用管）
w（权重向量）
-1.186453063332046
-0.5143822392120447

预测程序：

predict a1a.t a1a_model a1a_predict（a1a.t是官网下载的测试文件，a1a_predict是样本的预测值文件，里边存着预测值）

直接输出分类准确率，不用logistic函数再映射。

训练过程中损失函数随着迭代次数的变化：

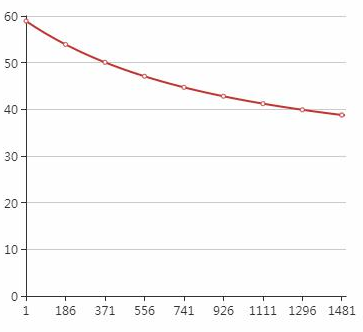
softmax回归：

logistic回归只能解决二分类问题，对于多分类问题怎么办呢？可以对logistic进行扩展，就是softmax回归，专门处理多分类问题。

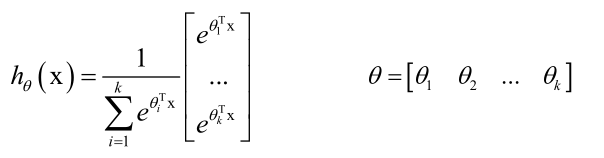
用一个θ先对特征向量x进行映射，然后再归一化，得到的值就是在0到1之间，和为1的概率值了。

怎么求θ呢？构造一个损失函数求解θ：

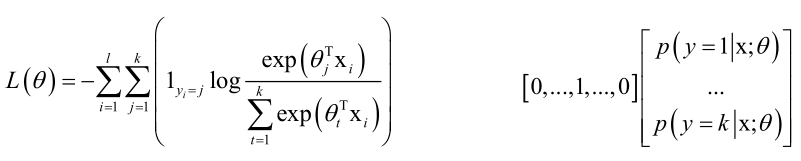
1_yi=j表示对于单个样本i，它如果属于j类就取1否则取0，同one-hot编码，所以里边的求和符号j从1到k所有项里边只有一项为1其他都为0，log里边是样本属于j类的概率值，这个函数也叫交叉熵损失函数。

后边的是，真实的标签值和softmax预测出来的标签值向量做内积，这两个向量越接近的话，拟合的越小，损失就越小。

上述问题也是一个凸优化问题，同样可以采取各种手段去处理它，这里采用梯度下降法：

对单个样本的梯度值：

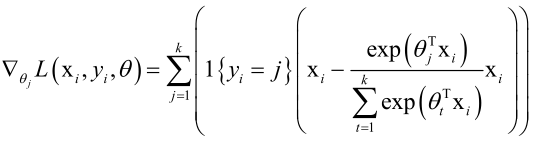
化简之后：

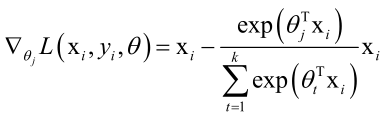
对于所有样本的梯度值，把上式累加起来就行了：

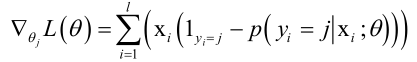
然后用梯度下降法更新就可以了。

实际应用：

logistic回归最经典的一个应用就是CTR预估（广告点击率预估click through rate），根据用户历史浏览行为（点击了哪些页面，浏览了哪些信息）预测他点击某个关键词（如牛奶）页面的概率值，这在搜索引擎和一些推荐系统里边是非常重要的，因为赚钱的核心就是让用户尽可能多的点击广告那样投广告的人才会为你付费，所以所每把广告提高一个百分点的话你的收入会增加很多了对于搜索引擎和互联网公司而言。

CTR预估技术的鼻祖是：

[1] Matthew Richardson, Ewa Dominowska, Robert J Ragno. Predicting clicks: estimating the click-through rate for new ads. international world wide web conferences. 2007. 它的核心就是特征工程，根据广告内容及用户行为怎么构造出一些有用的特征出来形成特征向量x，一旦这个特征向量形成之后，直接拿logistic回归去跑一遍就可以了。

logistic回归是一种很古老的算法，很多年前就已经出现了，[2] Daryl Pregibon. Logistic Regression Diagnostics. Annals of Statistics. 1981. 根据一个人的生命的特征诊断疾病（如血糖、血液来预判他有没有某种疾病）。

logistic是一个分类算法，而非回归算法，而且只能用于二分类问题，它的扩展版本softmax回归才能用来解决多分类问题。logistic回归是一个线性模型，其实就是算w^Tx这个东西。logistic回归是一个判别模型而不是生成模型，虽然他用了概率但是这个概率是假的，因为他从来没有假设样本x服从某种概率分布，他没有对p(y|x)或者说对p(x, y)进行建模，因此他本质上还是一种判别算法。

 本集总结：

首先回顾了线性模型，它的预测函数w^Tx+b。

然后引入了逻辑斯蒂回归LR它的基本思想：直接估计一个样本属于正样本的概率值。

然后引入了预测函数。

训练算法，用最大似然估计MLE，证明了是凸优化问题，这时用的正负样本标签为1、0，再用-1、1可以得到更简洁的版本。

加上L2、L1的正则化项，得到正则化的logistic回归。　

liblinear库。

logistic推广到多分类的情况，就是softmax回归，可以用于解决多分类问题。