树形DP(超详细!!!)
一、概念
1、什么是树型动态规划
树型动态规划就是在“树”的数据结构上的动态规划,平时作的动态规划都是线性的或者是建立在图上的,线性的动态规划有二种方向既向前和向后,相应的线性的动态规划有二种方法既顺推与逆推,而树型动态规划是建立在树上的,所以也相应的有二个方向:
- 叶->根:在回溯的时候从叶子节点往上更新信息
- 根 - >叶:往往是在从叶往根dfs一遍之后(相当于预处理),再重新往下获取最后的答案。
不管是 从叶->根 还是 从 根 - >叶,两者都是根据需要采用,没有好坏高低之分。
2、树真的是一种特别特别优美的结构!
用来做动态规划也简直是锦上添花再美不过的事,因为树本身至少就有“子结构”性质(树和子树);本身就具有递归性。所以在树上DP其实是其所当然的事,相比线性动态规划来讲,转移方程更直观,更易理解。
3、难点
- 和线性动态规划相比,树形DP往往是要利用递归+记忆化搜索。
- 细节多,较为复杂的树形DP,从子树,从父亲,从兄弟……一些小的要处理的地方,脑子不清晰的时候做起来颇为恶心
- 状态表示和转移方程,也是真正难的地方。做到后面,树形DP的老套路都也就那么多,难的还是怎么能想出转移方程,各种DP做到最后都是这样!
二、经典问题
【树的重心/质心】
对于一棵n个结点的无根树,找到一个点,使得把树变成以该点为根的有根树时,最大子树的结点数最小,即删除这个点后最大连通块的结点数最小。那么这个点就是树的重心。
例题:题目大意:对于一棵无根树,找到一个点使得树以该点为根的有根树,最大子树(选择该节点后其子树的最大节点)的节点数最小。

解法:任选一个结点为根,把无根树变成有根树,然后设f[i]表示以i为根的子树的结点个数。
程序实现:一次DFS,在无根树转有根树的同时计算。对于结点i,子树中最大结点个数为max{f[j]}个结点,i的“上方子树”中有n-f[i]个结点,只需在dfs过程中找到最大的子树节点,并与其上方的节点数做比较,就可以找出树的重心了。

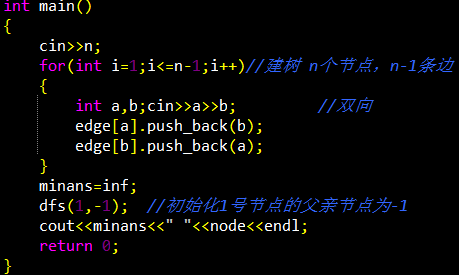
补充性质:
1.树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么他们的距离和一样。
2.把两个树通过一条边相连得到一个新的树,那么新的树的重心在连接原来两个树的重心的路径上
3.把一个树添加或删除一个叶子,那么它的重心最多只移动一条边的距离
【树的直径】
树的直径: 树的直径是指树的最长简单路。
例题:题目大意:对于一棵无根树,找到树的一条直径。假设边权为1。

解法一:从任意一点u出发搜到的最远的点一定是s、t中的一点,然后在从这个最远点开始搜,就可以搜到另一个最长路的端点,即用两遍广搜就可以找出树的最长路。
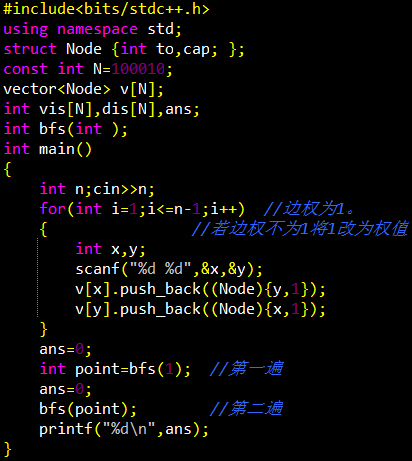

解法二:算是树的直径的一个性质,树的直径的长度一定会是某个点的最长距离f[i]与次长距离g[i]之和。最后求出max{f[i]+g[i]}就可以了。 令j是i的儿子,则:
1、若f[j]+dis[i][j]>f[i],则g[i]=f[i],f[i]=f[j]+dis[i][j];//最大值次大值被更新
2、否则,若f[j]+dis[i][j]>g[i],则g[i]=f[j]+dis[i][j];//次大值被更新
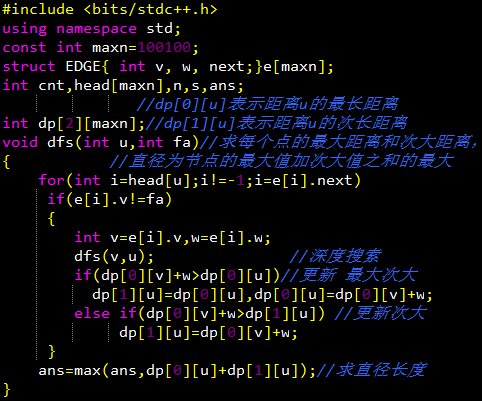

【树的中心】
首先题意是在一棵树T中输出每个结点到叶子的最远距离;

首先第一个dfs求出所有每个节点i在其子树中的正向最大距离和正向次大距离和d[i][0]和d[i][1](如果i节点在子树中最大距离经过了2号儿子,那么次大距离就是不经过2号儿子的最大距离)。并且还要标记c[i]=j表示节点i在其子树中的最大距离经过了节点j(即j是i的一个儿子)。
由上步我们获得了正向最大距离,正向次大距离和最大距离的儿子节点标记。画图可以知道我们建立的这棵树,i节点的最远距离只有两种选择:i节点所在子树的最大距离,或者i节点连接它的父节点所能到达的最大距离。
所以我们只要求出反向最大距离d[i][2](即i节点往它的父节点走所能到达的最大距离)就可以知道i节点在整个树中能走的最大距离了。 d[i][2]求法:i节点往它的父节j点走,如果它的父节点的正向最大距离不经过i的话,那么d[i][2]要不就是它父节点的反向最大距离+W[i][j]要不就是它父节点的正向最大距离+ W[i][j]. 如果它的父节点的正向最大距离经过i的话,那么d[i][2]要不就是它父节点的反向最大距离+W[i][j]要不就是它父节点的正向次大距离+ W[i][j].
上面就是dfs2要求的值。最终f[i]=max(d[i][0],d[i][2])
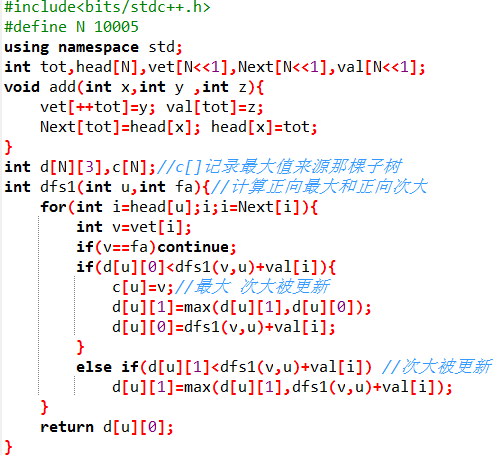

二、普通树形DP
普通的树形DP中,常常会采用叶->根的转移形式,根据父亲的状态,来确定子节点的状态,若子节点有多个,则需要一一枚举,将子节点(子树)的DP值合并。
P1352 没有上司的舞会
题目描述
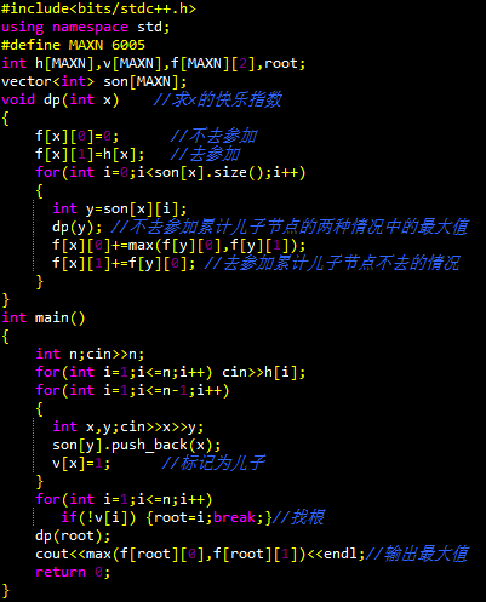
某大学有N个职员,编号为1~N。他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数Ri,但是呢,如果某个职员的上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
输入输出格式
输入格式:
第一行一个整数N。(1<=N<=6000) 接下来N行,第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127) 接下来N-1行,每行输入一对整数L,K。表示K是L的直接上司。
输出格式:
输出最大的快乐指数。


经典的树形dp
设f[x][0]表示以x为根的子树,且x不参加舞会的最大快乐值
f[x][1]表示以x为根的子树,且x参加了舞会的最大快乐值
则f[x][0]=sigma{max(f[y][0],f[y][1])} (y是x的儿子)
f[x][1]=sigma{f[y][0]}+h[x] (y是x的儿子)
先找到唯一的树根root 则ans=max(f[root][0],f[root][1])
P2015 二叉苹果树
【问题描述】
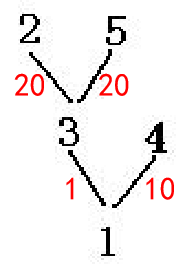
有一棵苹果树,如果树枝有分叉,一定是分2叉,这棵树共有N个结点,编号为1-N,树根编号一定是1。 现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。给定需要保留的树枝数量,求出最多能留住多少苹果。
【样例输入】
5 2
1 3 1
1 4 10
2 3 20
3 5 20
【样例输出】
21
【思路点拨】
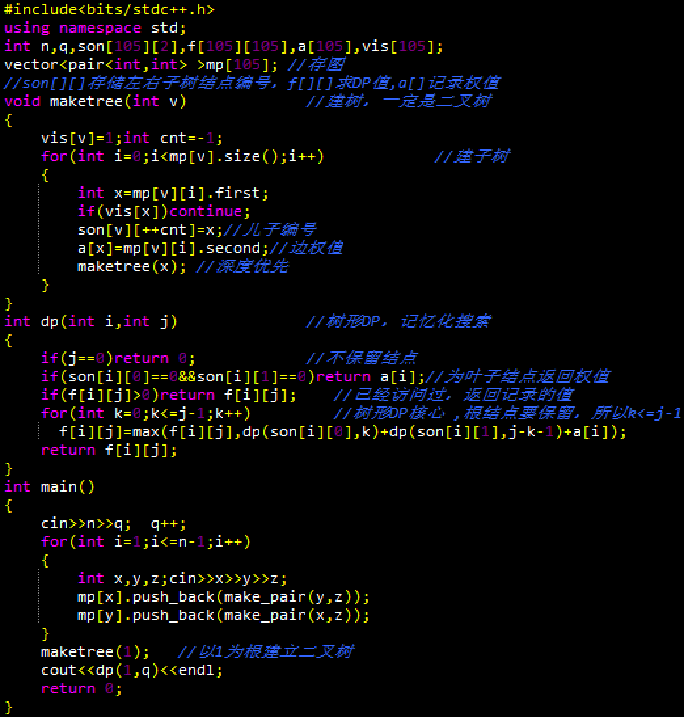
需要保留Q条树枝,即保留j=Q+1个结点。分三种情况讨论:
①全部保留右子树中的j-1个结点;//根结点必须保留
②全部保留左子树中的j-1个结点;
③左子树保留k个结点,则右子树保留j-k-1个结点。
设树根为i,左儿子为l[i],右儿子为r[i],对于①情况,要取得该方案的最大值,需要取得以r[i]为根的子树保留j-1个结点的最大值。②③同理。
f[i][j]:以i为根的树上保留j个节点的最大权值和。
状态转移方程:
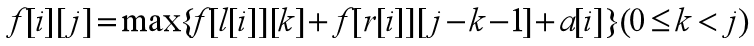
初始化:

目标: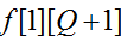
树形DP(超详细!!!)的更多相关文章
- 【二叉树-最长路径系列(任意路径)】直径、最长同值路径、 最大路径和(DFS、树形DP)
总述 这类题目都是求一个最长路径,这个路径可以不经过根节点. 使用dfs(即递归地遍历树)的方法.维护一个全局最长路径max作为最终结果,而递归方法dfs返回的是含根节点的最长路径.(若不使用全局变量 ...
- 【学习笔记】动态规划—斜率优化DP(超详细)
[学习笔记]动态规划-斜率优化DP(超详细) [前言] 第一次写这么长的文章. 写完后感觉对斜优的理解又加深了一些. 斜优通常与决策单调性同时出现.可以说决策单调性是斜率优化的前提. 斜率优化 \(D ...
- poj2486(树形dp)
题目链接:http://poj.org/problem?id=2486 题意:一颗树,n个点(1-n),n-1条边,每个点上有一个权值,求从1出发,走m步,最多能遍历到的权值. 分析:非常不错的树形d ...
- Day1:T3 bfs T4 树形DP
T3:BFS 回看了一下Day1的T3...感觉裸裸的BFS,自己当时居然没有看出来... 同时用上升和下降两种状态bfs即可 这一题还要注意一个细节的地方,就是题目要求的是求往返的最优解 k=min ...
- [SinGuLaRiTy] 树形DP专项测试
[SinGuLaRiTy-1015] Copyright (c) SinGuLaRiTy 2017. All Rights Reserved. 对于所有的题目:Time Limit:1s | Me ...
- 宝藏(树形DP)
这道题目是十分考验思维的,n^2应该还是比较好想的,主要是如何转移根的问题.转移根,在我看来应该是树形dp最难的一部分了, 一般学会如何转移根,也就差不多考验通吃树形dp了. 下面转一转大佬链接: ...
- hdu_1011(Starship Troopers) 树形dp
题目连接:http://acm.hdu.edu.cn/showproblem.php?pid=1011 题意:打洞洞收集脑子,你带领一个军队,洞洞互联成一棵树,每个洞中有一些bug,要全部杀死这些虫子 ...
- HDU 1520 树形DP入门
HDU 1520 [题目链接]HDU 1520 [题目类型]树形DP &题意: 某公司要举办一次晚会,但是为了使得晚会的气氛更加活跃,每个参加晚会的人都不希望在晚会中见到他的直接上司,现在已知 ...
- HDU 5977 Garden of Eden (树形dp+快速沃尔什变换FWT)
CGZ大佬提醒我,我要是再不更博客可就连一月一更的频率也没有了... emmm,正好做了一道有点意思的题,就拿出来充数吧=.= 题意 一棵树,有 $ n (n\leq50000) $ 个节点,每个点都 ...
随机推荐
- 将Excel表格数据转换成Datatable
/// <summary> /// 将Excel表格数据转换成Datatable /// </summary> /// <param name="fileUrl ...
- Word2Vector 中的 Hierarchical Softmax
Overall Introduction 之前我们提过基于可以使用CBOW或者SKIP-GRAM来捕捉预料中的token之间的关系,然后生成对应的词向量. 常规做法是我们可以直接feed DNN进去训 ...
- MySQL出现Waiting for table metadata lock的原因以及解决方法(转)
MySQL在进行alter table等DDL操作时,有时会出现Waiting for table metadata lock的等待场景.而且,一旦alter table TableA的操作停滞在Wa ...
- EF性能优化篇一
https://www.cnblogs.com/chenwolong/p/7531955.html 1.合理使用AsNoTracking 若对查询的数据不需要做任何修改,则可采用AsNoTrackin ...
- CSS box-sizing属性的正确用法
CSS自定义属性(变量) CSS box-sizing属性允许我们在元素的总宽度和高度中包含填充和边框. 没有CSS box-sizing属性 默认情况下,元素的宽度和高度计算如下: width + ...
- CMake编译的VS工程,安装时遇到错误:error MSB3073: 命令“setlocal
错误提示 70>CMake Error at src/base/cmake_install.cmake:63 (file): 70> file INSTALL cannot find 70 ...
- 查看 JVM 默认参数
-XX:+PrintFlagsFinal 可以获取所有可设置参数及值 获取 JVM 默认 Xss 大小 java -XX:+PrintFlagsFinal -version | grep Thread ...
- linux 进程通信之 mmap
一,管道PIPE 二,FIFO通信 三,mmap通信 创建内存映射区. #include <sys/mman.h> void *mmap(void *addr, size_t length ...
- Django类
django 1.中间件 中间件一般做认证或批量请求处理,django中的中间件,其实是一个类,在请求和结束后,django会根据自己的规则在合适的时机执行中间件中相应的方法, 如请求过来 执行p ...
- 目标检测的评价标准mAP, Precision, Recall, Accuracy
目录 metrics 评价方法 TP , FP , TN , FN 概念 计算流程 Accuracy , Precision ,Recall Average Precision PR曲线 AP计算 A ...
