tensorflow2.0 学习（二）

线性回归问题

 # encoding: utf-8

 import numpy as np
 import matplotlib.pyplot as plt

 data = []
 for i in range(100):
     x = np.random.uniform(-10., 10.)    #均匀分布产生x
     eps = np.random.normal(0., 0.01)    #高斯分布产生一个误差值
     y = 1.477*x + 0.089 +eps            #计算得到y值
     data.append([x, y])                 #保存到data中

 data = np.array(data)                   #转成数组的方式方便处理
 plt.plot(data[:,0], data[:,1], 'b')    #自己引入用于观察原始数据
 #plt.show()
 plt.savefig('original data.png')

 def mse(b, w, points):                  #计算所有点的预测值和真实值之间的均方误差
     totalError = 0
     for i in range(0, len(points)):
         x = points[i, 0]
         y = points[i, 1]
         totalError += (y -(w*x + b))**2     #真实值减预测值的平方
     return totalError/float(len(points))    #返回平均误差值

 def step_gradient(b_current, w_current, points, lr):    #预测模型中梯度下降方式优化b和w
     b_gradient = 0
     w_gradient = 0
     M = float(len(points))
     for i in range(0, len(points)):
         x = points[i, 0]
         y = points[i, 1]
         b_gradient += (2/M) * ((w_current*x + b_current) - y)   #求偏导数的公式可知
         w_gradient += (2/M)*x*((w_current*x + b_current) - y)   #求偏导数的公式可知
     new_b = b_current - (lr*b_gradient)      #更新参数，使用了梯度下降法
     new_w = w_current - (lr*w_gradient)      #更新参数，使用了梯度下降法
     return [new_b, new_w]

 def gradient_descent(points, starting_b, starting_w, lr, num_iterations):   #循环更新w,b多次
     b = starting_b
     w = starting_w
     loss_data = []
     for step in range(num_iterations):  #计算并更新一次
         b, w = step_gradient(b, w, np.array(points), lr)        #更新了这一次的b,w
         loss = mse(b, w, points)
         loss_data.append([step+1, loss])
         if step % 50 == 0:              #每50次输出一回
             print(f"iteration:{step}, loss{loss}, w:{w}, b:{b}")
     return [b, w, loss_data]

 def main():
     lr = 0.01               #学习率，梯度下降算法中的参数
     initial_b = 0           #初值
     initial_w = 0
     num_iterations = 1000   #学习100轮
     [b, w, loss_data] = gradient_descent(data, initial_b, initial_w, lr, num_iterations)
     loss = mse(b, w, data)
     print(f'Final loss:{loss}, w:{w}, b:{b}')

     plt.figure()            #观察loss每一步情况
     loss_data = np.array(loss_data)
     plt.plot(loss_data[:,0], loss_data[:,1], 'g')
     plt.savefig('loss.png')
     #plt.show()

     plt.figure()        #观察最终的拟合效果
     y_fin = w*data[:,0] + b + eps
     plt.plot(data[:,0], y_fin, 'r')
     #plt.show()
     plt.savefig('final data.png')

 if __name__ == '__main__':
     main()

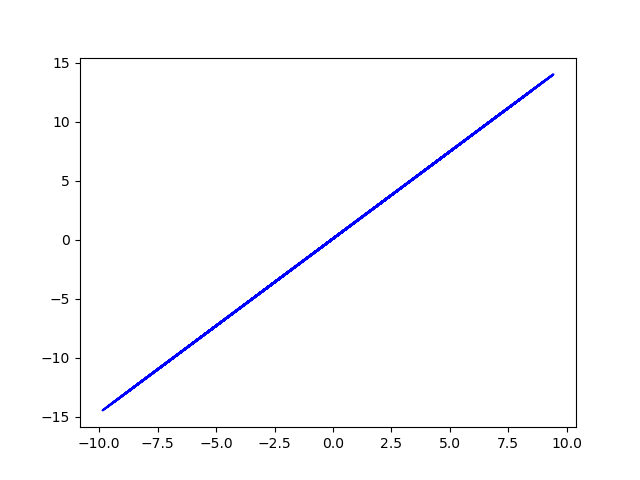
original data (y = w*x + b +eps)

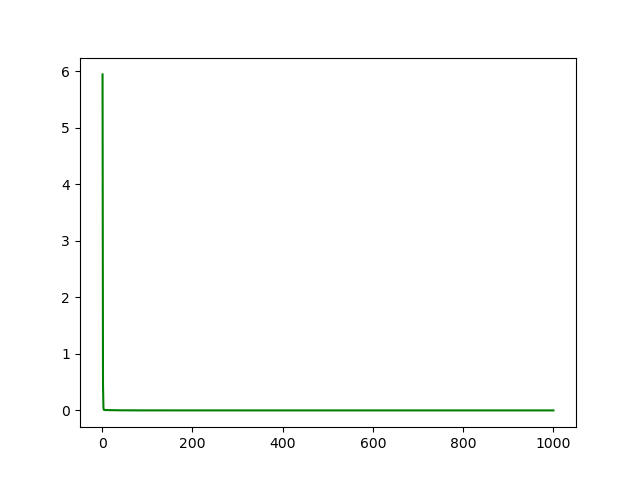
loss rate

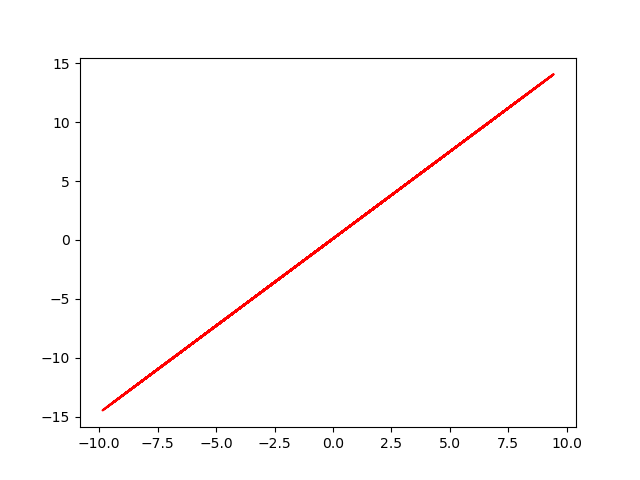
final data (y' = w' *x + b' + eps )

最终loss趋近9.17*10^-5, w趋近1.4768, b趋近0.0900

真实的w值1.477， b为0.089

对于线性回归问题，适用性挺好！

主要的数学代码能理解，唯有取梯度的反方向更新参数，不是很能理解！

这里还没有用到tensorflow，下一次更新基础知识！