[基础]斯坦福cs231n课程视频笔记(三) 训练神经网络
\
training Neural Network
一般以mini-batch的形式训练,类似于cs231n中assignment的格式 简单举个例子,
for epoch in range(epochs):
#每个周期训练一遍所有数据
for iteration in range(iterations):
#每次迭代只从训练数据集中采样一小批 作为当前训练数据
minibatch = sample(train_dataset)
x, y = minibatch['x'], minibatch['y']
#经过网络输出预测结果
y_pred = net(x)
#计算和预期结果的误差
loss = loss_function(y_pred, y)
#利用BP和计算图 计算误差回传梯度
gradients = compute_gradient(loss)
#更新网络参数
net.params = update_params(net.params, gradients)
Activation function

\
注意,激活函数是用在线性之后:
- 即\(\sigma(f(x)) = \sigma(wx+b)\) 只是有时候会简单记做 $\sigma(x) $
- 因此,反向传播时,如果$\frac{\partial\ \sigma}{\partial f(x)} \approx0, $ 则后续的传播$ \frac{\partial \ \sigma}{\partial w} = \frac{\partial \ \sigma}{\partial f(x) } \cdot\frac{\partial f(x)}{\partial w} \approx 0 $
一篇对激活函数更细致的总结 在cs231n笔记基础上的解释 https://zhuanlan.zhihu.com/p/25110450
sigmoid
两个缺点:
(1) 饱和使梯度消失,在输入为正的较大值或是负的较大值时,反向传播得到的梯度几乎为零,最终会导致越往后传梯度消失 因为链式法则涉及到梯度相乘
(2) sigmoid的输出不是零中心的,意味着如果输入总是为正数 那么关于参数w的梯度在反向传播时要么全为正 要么全为负(具体依表达式f而定),这会导致参数用梯度下降法更新时,呈现z字型下降,如下图:
- 假设w=(w1,w2) 有两个维度,由于全为正或全为负 则必须要在一三象限,而假设最优的权重应该在第四象限的蓝色向量上,那么更新的路径 假设从第一象限出发,会大概类似于红色z字型的路线 即更新的路径十分曲折 不够高效。https://liam.page/2018/04/17/zero-centered-active-function/
- 同样的,这也是为什么我们希望输入数据是零均值的,也就是输入数据里面正负数是均衡的

\
ReLU
缺点:
(1)也具有饱和的问题,在输入x落在负半轴时,输出总是零,从而参数的梯度反传时得到的为零
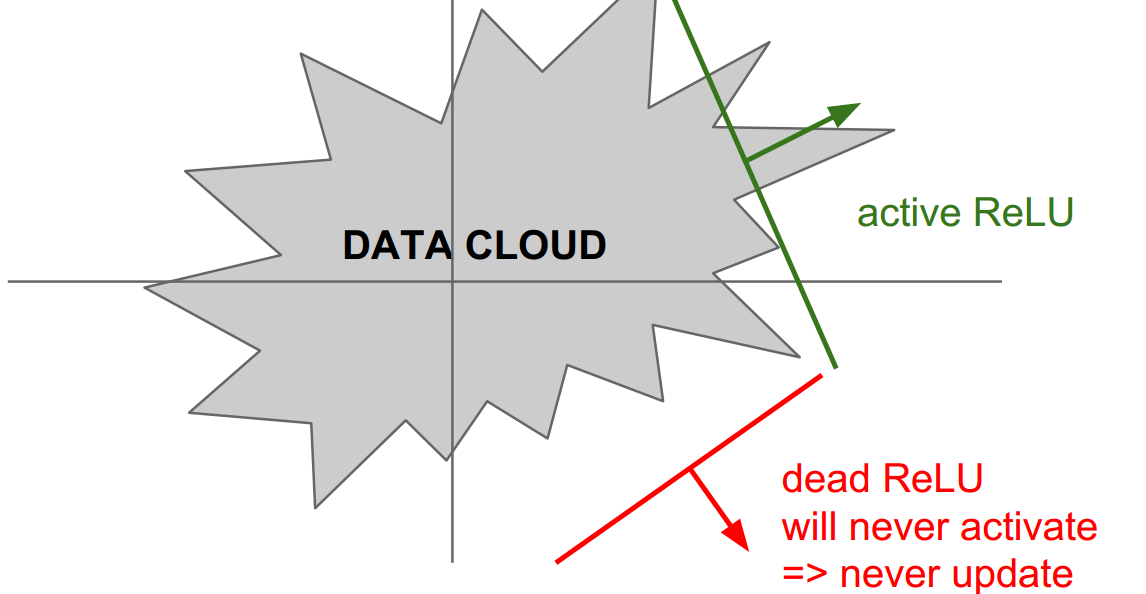
(2)在训练的时候,ReLU单元比较脆弱并且可能“死掉”。举例来说,当一个很大的梯度流过ReLU的神经元的时候,可能会导致梯度更新到一种特别的状态,在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生,那么从此所以流过这个神经元的梯度将都变成0。也就是说,这个ReLU单元在训练中将不可逆转的死亡,因为这导致了数据多样化的丢失。例如,如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。比如:
- 同样是假设 w = (w1,w2),参数有两维,如果最优的参数落在2、3、4象限,那么用ReLU无法在参数更新的过程中收敛到最优,而如果落在第一象限则可以。
\
Preprocessing
下面主要说预处理里面的归一化 normalization:
- 归一化就是将原本散乱的数据归一成零均值、方差为1,zero mean ,unit variance的操作,由此数据的中心大致处于D维空间的零中心
- 归一化的作用 可以使得分类器更鲁棒,对于微小的扰动不会过于敏感
【注意】
在归一化等预处理操作,应该先将原始数据分成训练集、验证集、测试集
然后使用训练集的数据来计算均值和方差等归一化需要用到的量,
- 在训练的初始阶段,对整个训练集做归一化;
- 在测试阶段,将在训练集上计算的量(比如训练集的均值或方差)应用到测试样本上做归一化。
训练阶段和测试阶段必须使用的是同一种归一化操作。
https://www.zhihu.com/question/312639136 解释了为什么预处理时要先分成训练集、验证集和测试集,而不是对所有数据预处理完再分成训练集、验证集和测试集
Batch Normalization
一篇比较好的解释 https://blog.csdn.net/hjimce/article/details/50866313 https://www.cnblogs.com/eilearn/p/9780696.html
文中介绍的BN的motivation:
神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。
我们知道网络一旦train起来,那么参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中,数据分布的改变称之为:“Internal Covariate Shift”。
Paper所提出的算法,就是要解决在训练过程中,中间层数据分布发生改变的情况,于是就有了Batch Normalization,这个牛逼算法的诞生。
与在训练初始阶段将所有输入归一化不同,BN相当于在forward pass里的每一层激活函数之前进行归一化(即先通过线性映射计算y=wx+b,然后对y进行归一化,再输入到激活函数)
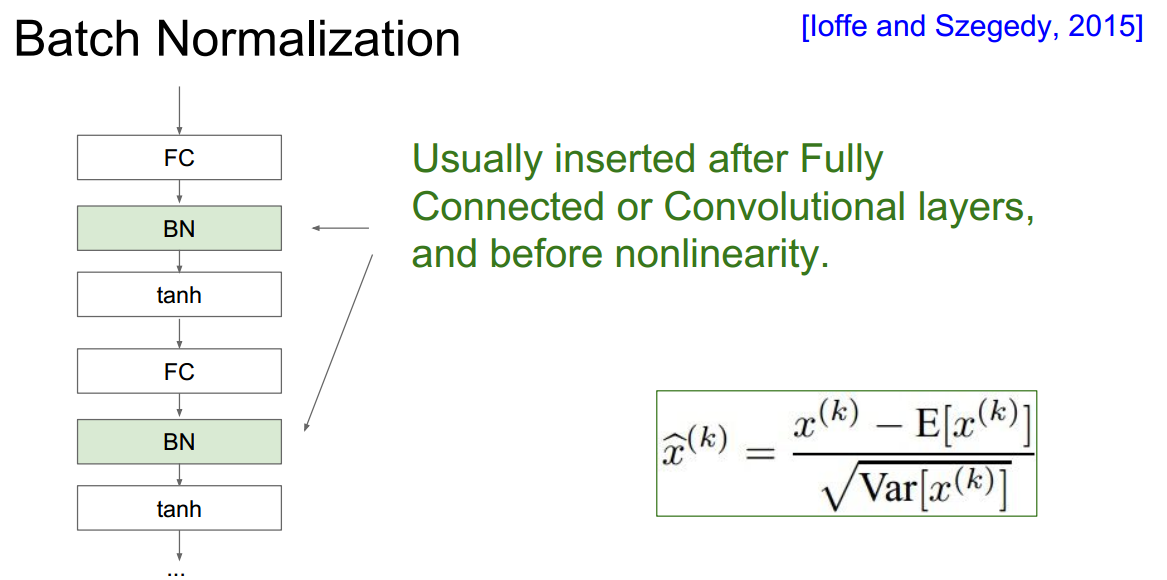
\
为什么BN里要用scale and shift?
在归一化到零均值zero mean, 标准方差unit variance之后,本层学习到的特征可能会发生改变
对归一化的结果进行scale and shift,有可能会复原到原本学习到的特征,
- 其中scale和shift的参数是可以学习的,因而可以将标准分布调整到网络想要的分布

\
如何将训练时计算的均值和方差用于测试阶段?
用moving average
可以理解为每次更新running mean相当于把之前的值衰减一些(* momentum),然后把当前的mini-batch sample mean加进去一部分(* (1-momentum))。其实也就是一阶指数平滑平均。
\
BN的好处?
- improve gradient flow through the network 什么意思?
- allows high learning rates 为什么?
- 减少对好的初始化的依赖,也就是即使权重初始化不够好用BN能尽量减少影响
- 是一种正则化的形式,可能还能减少对dropout的需要
权重初始化 Weight Initialization
如果权重一开始都初始化为零,那么多数神经元都会死亡(因为梯度变为零)
还有一个问题,由于所有权重都是一样的值(这里不一定是零,也可以试试全都初始化为某个值),由于计算方式相同,可能达不到学习不同特征的目的
交叉验证 Cross Validation

\
课程作业中也遇到这个问题,如果学习率设置得太大,会导致loss爆炸
虽然是沿着梯度方向走,但是未必是刚好指向到最优点 可能只是直接指向最优点方向的左右扰动
如果这时候学习率设置得大 也就是步长大 可能会带来反效果
交叉验证的策略:
从粗调参数到精调:
粗调时 只用a few epochs来了解参数大致的在什么范围表现最好
精调时则需要更长的训练时间
一个检测 loss 是否爆炸的技巧 如果随着训练不断进行 loss会增长到3倍于初始loss 则应该及时break out 这意味着参数不合适
一次最好只调两到三个超参数,先把它们调好再去调其他的。learning_rate的优先级应该较高
表现较好的参数不能刚好位于所选参数范围的边界,否则会导致错过那些表现更好的参数,应尽可能使最优参数位于所选范围的中间
另一个可以跟踪的值:参数更新的幅度/参数的magnitude,也就是参数更新的幅度相比于参数本身的值来说有多大
param_scale = np.linalg.norm(W)
update = -learning_rate*dW
update_scale = np.linalg.norm(update)
print(update_scale/param_scale)
\
参数更新方法 Parameter Update
- 将最优化的过程看做是质点从山上往最低处走,随机初始化参数可看做将质点放在山上的某个高处作为起点:
SGD
超参数是learning_rate
认为梯度直接影响质点的位置
w += learning_rate * dw
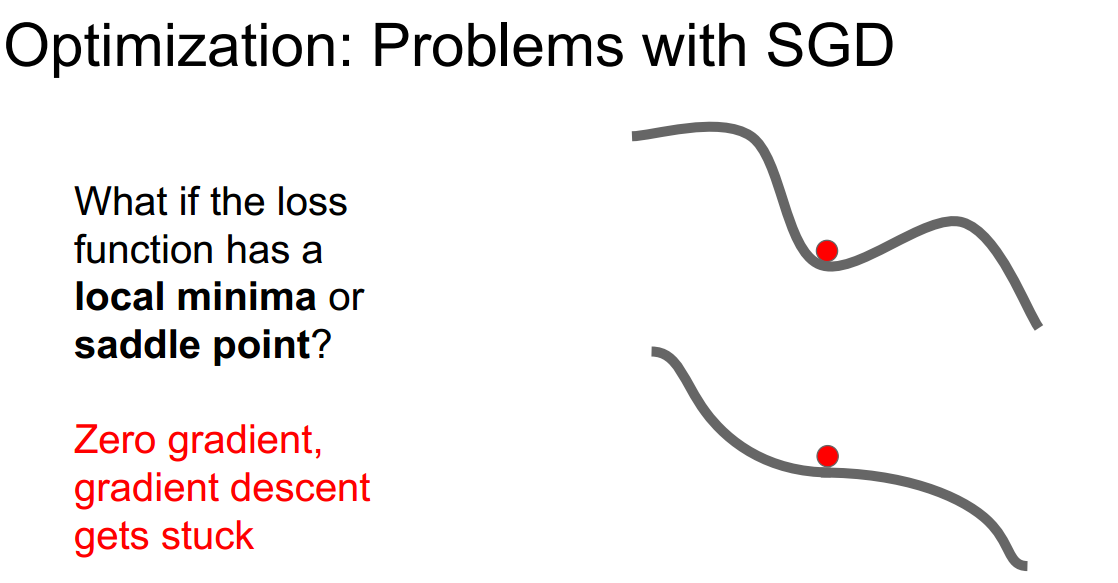
容易使loss陷入局部最优local minima或是马鞍点saddle point ,在这类地方 梯度都为零,无法更新,因此会stuck
由于是随机的stochastic,每次只是在minibatch上计算loss和梯度 来代表所有数据的loss和梯度,但是不一定准确 很容易被噪声影响,从而使得收敛的过程十分曲折
\
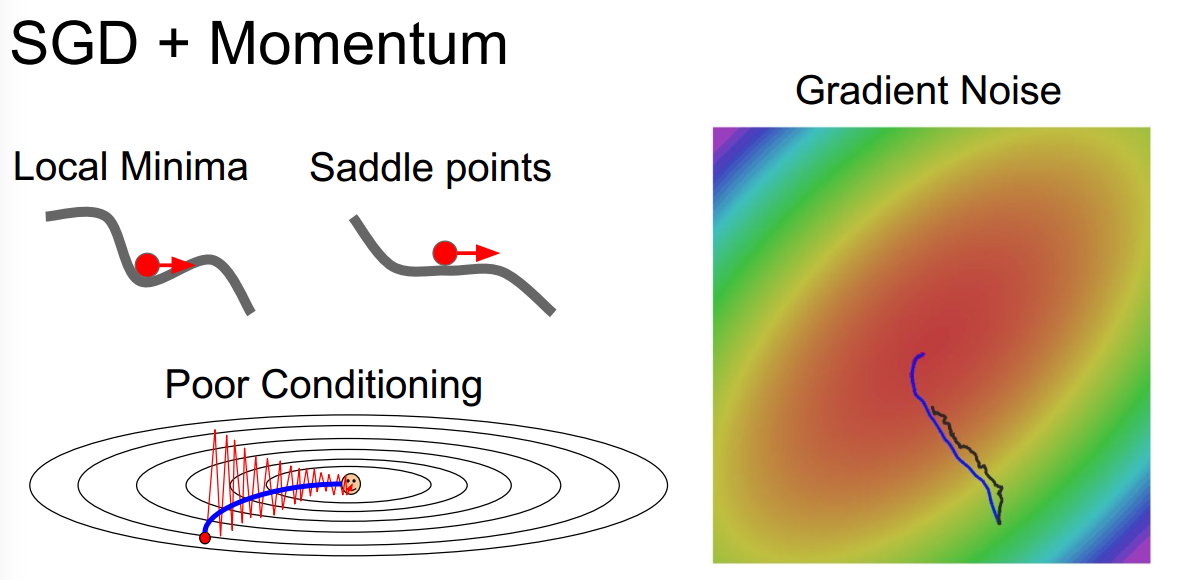
SGD+momentum
超参数是learning_rate, momentum
认为梯度直接影响的是速度,而速度再影响位置
v += momentum * v - learning_rate * dw #其中momentum可看作摩擦系数
w += v #理解速度影响位置:其实可以看作 w += v*dt , 而dt=1 一段很短的时间
参数会在任何有持续梯度的方向上增加速度
引入速度,可以一定程度上解决陷入局部最优或陷入马鞍点的问题
速度可以看做是 weighted sum of gradients over time 只不过这里更新时间是在指数级的位置,因此越久之前的梯度 权重越小 越靠近当前时刻的梯度 权重越大。【时间序列分析中的移动平均法?】
\
Adagrad
引入grad_square作learning_rate的分母,从而让梯度大的参数更新幅度慢一些,梯度小的参数更新幅度快一些
grad_square += dx**2 #累加每次更新时的梯度平方
x += -learning_rate * dx / (np.sqrt(grad_square)+eps) #eps用于平滑 避免分母为零
# 当dx较高,则cache较高,在更新x的式子中,分母变大,因而梯度前的系数变小 更新的幅度减弱
局限是由于分母grad_square是累加的,随着时间慢慢变大,整个步长即更新幅度都会慢慢变小,如果在凸优化的环境中 这是比较好的 但对于非凸优化来说,容易导致陷入saddle point等问题
RMSprop
解决Adagrad 随着时间进行 步长慢慢变小的问题,对grads_square的更新不再是简单的累加,而是使用类似momentum的更新方法【weighted sum】
grad_square = momentum*grad_square + (1 - momentum)*dx**2 #momentum一般取0. 99
x += -learning_rate * dx / (np.sqrt(grad_square)+eps)
Adam
综合考虑RMSprop 和 momentum 即梯度的一阶和二阶
grad = beta1 * grad + (1 - beta1) * dx
grad_square = beta2 * grad_square + (1 - beta2) * dx**2
x += -learning_rate * grad / (np.sqrt(grad_square)+eps)
Adam的完整形式还考虑了偏置的更新

\
\
以上这些都只是在研究如何更好地使training loss达到最优,但其实我们更应该关心的是how it performance on unseen data,换句话说就是缩小train_acc和val_acc之间的距离
\
改善过拟合 Overfiting
模型集成 Model ensemble
将多个模型的测试结果平均作为最终的预测结果。
trick,有时候不一定要各自训练N个模型然后将它们的结果平均,只需要训练一个模型,然后在训练过程中将不同时期的模型保存下来 snapshot
另一个trick,并不一定需要记录多个模型,只需要在训练过程中对参数计算moving average,然后在测试时作为该模型的参数使用即可【因为记录多个模型归根结底是要分别用各个模型的参数来计算结果】 small trick, but not too common in practice
Instead of using actual parameter vector, keep a moving average of the parameter vector and use that at test time
正则化 Regularization
除了前面介绍过的Batch Normalization,dropout也是正则化的一种方法,在训练的时候对网络中的神经元随机失活,可以看做是原本完整网络的一个子采样 subset ,但是在测试的时候并不引入随机性【否则可能会导致同样的输入但是测试结果每次都不太一样。。不稳定。。】
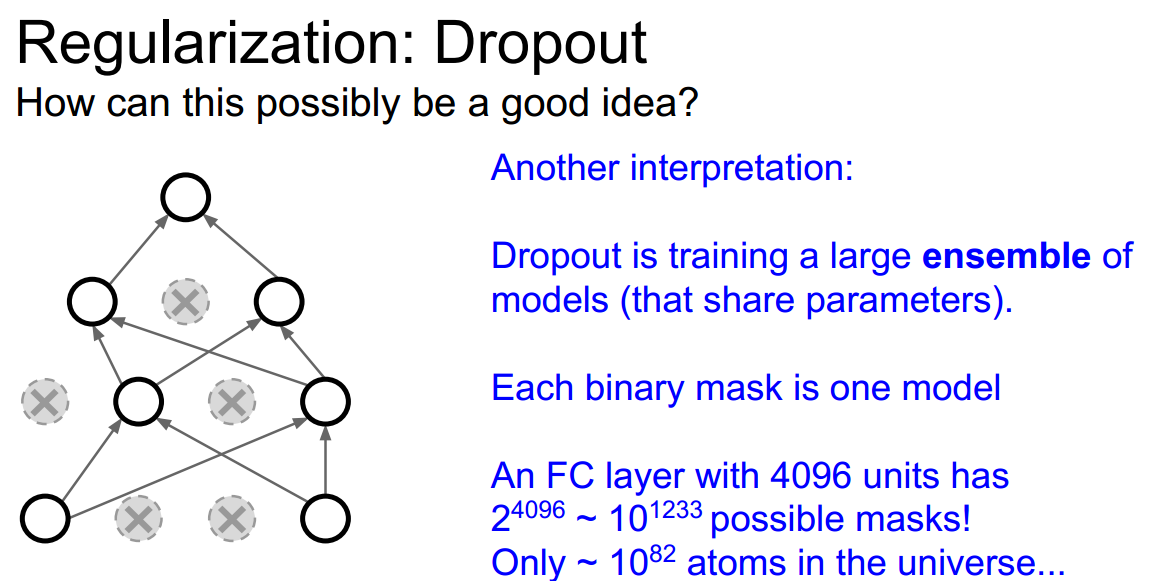

dropout的一个trick:inverted dropout:
使得test时保持高效
如果不用inverted 需要在test时额外乘上dropout的概率,会带来额外的计算,而用inverted把改动放在训练的时候则test可以不做任何额外改动
\
正则化的一般套路:
在训练的时候添加一些随机性进去,使其training表现可能比原完整网络时下降 但是test时可能表现得比原来完整时好,避免过拟合,提高泛化能力

\
有必要同时使用多种正则化方法吗?
一般来说 Batch Normalization就够了,如果 BN还不够就加入dropout;
而且正则化中的参数一般不是blind cross-validation来调参,而是观察到过拟合之后加入正则化
You generally don't do a blind cross-validation over these things, instead you add them in a targeted way once you see your network is overfitting
迁移学习 Transfer Learning
有时候过拟合是因为数据不够多,可以先用一个已经在大数据集上训练好的模型,然后在自己的小数据集上微调 fine-tune
具体从什么地方开始调,有以下表格的四种情况,一般微调的时候需要冻结(freez)其它层 保持它们的参数不变
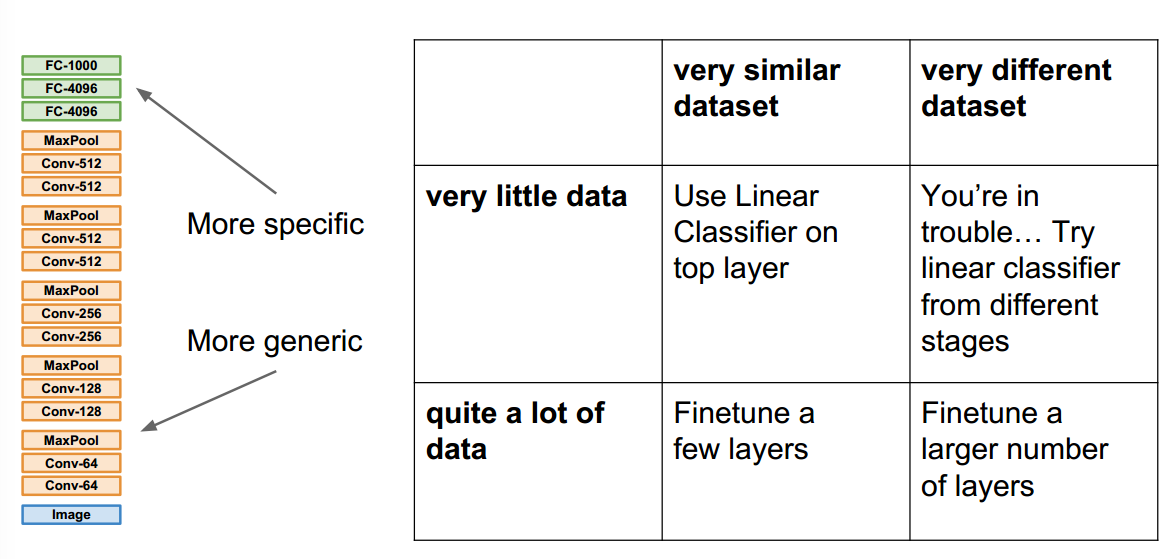
\
如果你的数据集和ImageNet差不多(very similar dataset) 都是动物图片之类的,而且你的数据集比较小(very little data),则可以只对linear classifier的最后一层进行训练,如下图的第二点所示
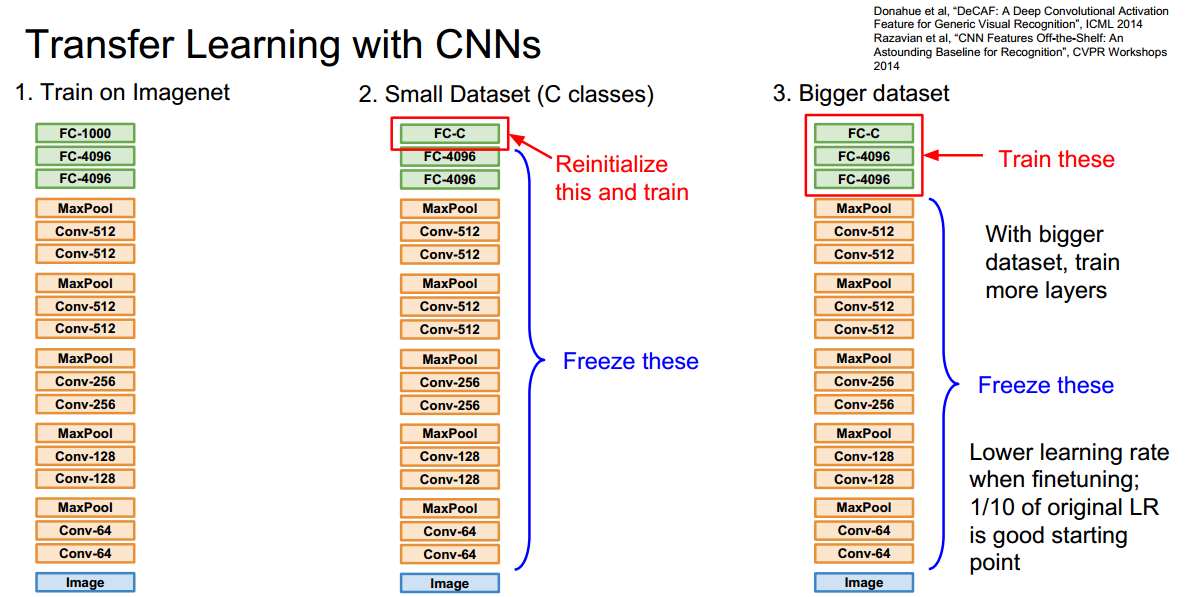
[基础]斯坦福cs231n课程视频笔记(三) 训练神经网络的更多相关文章
- [基础]斯坦福cs231n课程视频笔记(一) 图片分类之使用线性分类器
线性分类器的基本模型: f = Wx Loss Function and Optimization 1. LossFunction 衡量在当前的模型(参数矩阵W)的效果好坏 Multiclass SV ...
- [基础]斯坦福cs231n课程视频笔记(二) 神经网络的介绍
目录 Introduction to Neural Networks BP Nerual Network Convolutional Neural Network Introduction to Ne ...
- 转:深度学习斯坦福cs231n 课程笔记
http://blog.csdn.net/dinosoft/article/details/51813615 前言 对于深度学习,新手我推荐先看UFLDL,不做assignment的话,一两个晚上就可 ...
- 《分布式Java应用之基础与实践》读书笔记三
对于大型分布式Java应用与SOA,我们可以从以下几个方面来分析: 为什么需要SOA SOA是什么 eBay的SOA平台 可实现SOA的方法 为什么需要SOA 第一个现象是系统多元化带来的问题,可 ...
- 斯坦福机器学习视频笔记 Week4 & Week5 神经网络 Neural Networks
神经网络是一种受大脑工作原理启发的模式. 它在许多应用中广泛使用:当您的手机解释并理解您的语音命令时,很可能是神经网络正在帮助理解您的语音; 当您兑现支票时,自动读取数字的机器也使用神经网络. Non ...
- 斯坦福机器学习课程 Exercise 习题三
Exercise 3: Multivariate Linear Regression 预处理数据 Preprocessing the inputs will significantly increas ...
- Linux入门视频笔记三(常用工具集)
一.全局变量(Linux中的全局变量指在整个系统中都能用的变量) 1.USER:当前登录系统的用户的用户名 2.HOME:当前用户的主目录 cd $HOME 或 cd ~可以进入用户主目录 3.PAT ...
- CS231n课程笔记翻译9:卷积神经网络笔记
译者注:本文翻译自斯坦福CS231n课程笔记ConvNet notes,由课程教师Andrej Karpathy授权进行翻译.本篇教程由杜客和猴子翻译完成,堃堃和李艺颖进行校对修改. 原文如下 内容列 ...
- CS231n课程笔记翻译5:反向传播笔记
译者注:本文智能单元首发,译自斯坦福CS231n课程笔记Backprop Note,课程教师Andrej Karpathy授权翻译.本篇教程由杜客翻译完成,堃堃和巩子嘉进行校对修改.译文含公式和代码, ...
随机推荐
- C# 深入分析 GC 处理机制
引用地址:https://www.cnblogs.com/nele/p/5673215.html GC的前世与今生 虽然本文是以.NET作为目标来讲述GC,但是GC的概念并非才诞生不久.早在1958年 ...
- Mybatis的XML映射文件(四)
MyBatis 的真正强大在于它的映射语句,也是它的魔力所在.由于它的异常强大,映射器的 XML 文件就显得相对简单.如果拿它跟具有相同功能的 JDBC 代码进行对比,你会立即发现省掉了将近 95% ...
- 对象锁和class锁
对象锁:就是这个锁属于这个类的对象实例,可以通过为类中的非静态方法加synchronized关键字 或者使用 synchronized(this) 代码块,为程序加对象锁. Class锁:就是这个锁属 ...
- 史上最全的LaTeX特殊符号语法
史上最全的LaTeX特殊符号语法 运算符 语法 效果 语法 效果 语法 效果 + \(+\) - \(-\) \triangleleft \(\triangleleft\) \pm \(\pm\) \ ...
- vue2.x 监听数据变化 ---- watch
computed: { //需要监听的数据 loginToken () { return this.$store.state.userinfo.status; } }, watch: { loginT ...
- Angular 4.x NgClass ngStyle 指令用法
<some-element [ngClass]="'first second'">...</some-element> <some-element [ ...
- Note | PyTorch
目录 0. 教程和笔记 1. 模型操作 2. 网络设计 卷积图示 填充(padding) 升采样 全连接层 3. 损失函数 交叉熵 4. 系统或环境交互 模型加载 5. 犯过的错误 损失异常 测试显存 ...
- IPv6 地址生命周期
在preferred time和valid lifetime之间叫做deprecated 状态,当地址达到这个时间段的时候,地址不能主动的发起连接只能是被动的接受连接,过了valid lifetime ...
- MySQL中的存储过程、函数与触发器
一.对待存储过程和函数的态度 优点: 1.存储过程只在创建时进行编译,sql语句则每次执行都需要编译.能提高数据库执行速度. 2.简单复杂操作结合事物一起封装. 3.复用性高. 4.安全性高,可指定存 ...
- EF直接更新数据(不需查询)
//0.0创建修改的 实体对象 Models.BlogArticle model = new BlogArticle(); model.AId = ; model.ATitle = "新的数 ...
