FFT求卷积（多项式乘法）

卷积

如果有两个无限序列a和b，那么它们卷积的结果是：$y_n=\sum_{i=-\infty}^\infty a_ib_{n-i}$。如果a和b是有限序列，a最低的项为a0，最高的项为an，b同理，我们可以把a和b超出范围的项都设置成0。那么可以得出：y0=a0b0，y1=a1b0+a0b1，y2=a0b2+a1b1+a2b0……，y(n+m)=a(n)b(m)。

构造两个多项式A(x)和B(x)：

$A=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}+a_nx^n$，

$B=b_0+b_1x+b_2x^2+...+b_{m-1}x^{m-1}+b_mx^m$。

那么$A(x)*B(x)=C(x)=a_0b_0+(a_0b_1+a_1b_0)x+...+a_nb_mx^{n+m}$，把系数提取出来，可以发现两序列卷积可以转换为用序列作系数进行多项式乘法。

多项式

一个多项式既可以用系数表示，也可以用点值表示。n个点可以表示一个n-1次多项式。

如果用系数表示法来多项式乘法，时间复杂度是$O(n^2)$的，而用点值表示法只需要$O(n)$的时间。然而我们需要的是系数表示法。所以我们需要找到一个优秀的算法将它们两者转换，这就是（我们眼中的）FFT。

复数

设$i^2=-1$，a，b为实数，形如$a+bi$的数叫做复数。

用x轴表示a的大小，y轴表示b的大小，构造出的平面直角坐标系叫做复平面。复数的模长是原点到$(a, b)$的距离，即$\sqrt{a^2+b^2}$。复数的辐角即为以逆时针为正方向，从x轴正半轴到已知向量的转角。

复数的加减法则是显然的，可以看作向量的加减。

复数可以写成$N(cos\alpha+isin\alpha )$，$\alpha$表示复数的辐角。设$z_1=A(cos\alpha + isin\alpha)$，$z_2=B(cos\beta + isin\beta)$，那么$z_1z_2=AB[(cos\alpha cos\beta-sin\alpha sin\beta)+i(sin\alpha cos\beta+cos\alpha sin\beta)]=AB[cos(\alpha+\beta)+isin(\alpha+\beta)]$。也就是说，两复数相乘，模长相乘，辐角相加。如果写成普通形式的话，就是$(a+bi)(c+di)=(ac-bd)+(bc+ad)i$。

单位根

在复平面上，以原点为圆心，1为半径作圆，所得得圆为单位圆。从x轴正半轴开始将圆n等分，联向第一个等分点所代表的复数$\omega_n$叫做n次单位根，意思是说$w_n$的n次方为1（根据复数的乘法运算法则）。可以推得，其他等分点代表的向量为$\omega_n^1$,$\omega_n^2$……，一直到$\omega_n^n = \omega_n^0=1$。显然$\omega_n^k=cosk*\frac{2\pi}{n}+isink*\frac{2\pi}{n}$。

单位根有几个性质：

消去引理：$\omega_{2n}^{k+n}=-\omega_{2n}^k$。这是最重要的性质，使得分叉个数为2。
折半引理：${(\omega_n^k)^2}={\omega_{n/2}^k}$。这保证了FFT中子问题和原问题的规模都是n。
求和引理：$\sum_{i=0}^{n-1}(\omega_n^k)^i=\left\{ \begin{aligned} 0, n\nmid k \\ n, n\mid k \end{aligned} \right.$这是用来证明逆变换的。

DFT

前面说过，DFT是要把多项式的系数表达转成点值表达。设多项式A(x)的系数为$(a_o,a_1,a_2,\ldots,a_{n-1})$，那么

$A(x)=a_0+a_1*x+a_2*{x^2}+a_3*{x^3}+a_4*{x^4}+a_5*{x^5}+ \dots+a_{n-2}*x^{n-2}+a_{n-1}*x^{n-1}$

将下标按照奇偶性分类，那么：$A(x)=(a_0+a_2*{x^2}+a_4*{x^4}+\dots+a_{n-2}*x^{n-2})+(a_1*x+a_3*{x^3}+a_5*{x^5}+ \dots+a_{n-1}*x^{n-1})$

设：

$A_1(x)=a_0+a_2*{x}+a_4*{x^2}+\dots+a_{n-2}*x^{\frac{n}{2}-1}$

$A_2(x)=a_1+a_3*{x}+a_5*{x^2}+ \dots+a_{n-1}*x^{\frac{n}{2}-1}$

那么：$A(x)=A_1(x^2)+xA_2(x^2)$

根据单位根的性质，将前面一半的值带入可得：

$A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})=A_1(\omega_{\frac{n}{2}}^{k})+\omega_n^kA_2(\omega_{\frac{n}{2}}^{k})$(折半引理的作用：将问题分解成条件完全相同的子问题)

同理带入后面的值：

$A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}(\omega_n^{2k+n})=A_1(\omega_n^{2k})-\omega_n^kA_2(\omega_n^{2k})$(消去引理：使得分叉个数为2。如果没有这个引理的话，就必须再去算一遍$A(\omega_n^{k+\frac{n}{2}})$的值，分叉个数变成4了。)

由于这两个式子只有加号减号不同，我们只需计算前面一半的点值即可。这样就将问题规模缩小了一半。当n=1时，点值是一个常数，直接返回即可。不难看出这是一个分治算法，时间复杂度为$O(nlogn)$。

为IDFT作准备

我们发现，FFT其实是在求下图的$y_i$：（实在打不出来qwq）

那么现在的问题是，已知$y_i$，如何推回$a_i$？

由于我太弱了，继续上图吧。。

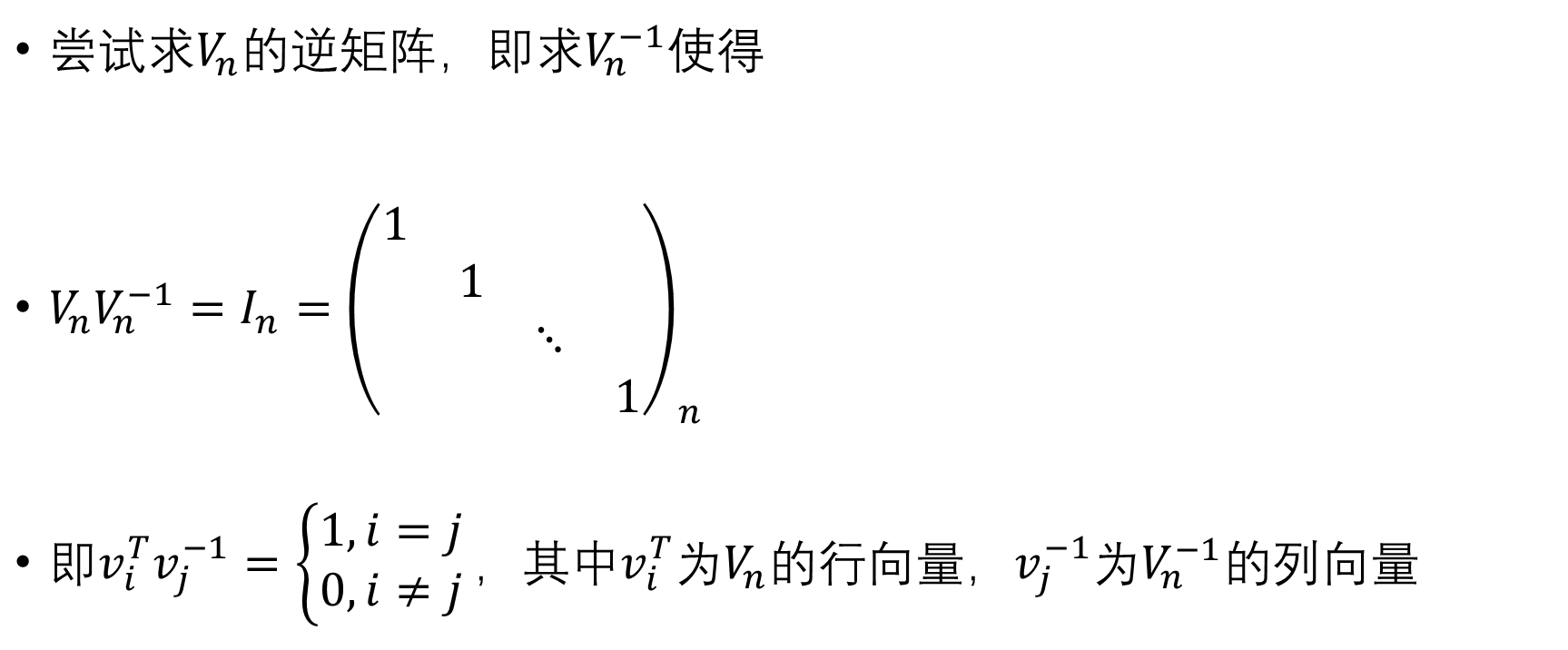
（补充一下，只要求出那个范德蒙德行列式的逆矩阵，乘在等式两边，那么就可以通过$y_i$推出$a_i$）

怎么构造$V^{-1}$，使得$v_i^Tv_j^{-1}=\left\{ \begin{aligned} 1, i=j \\ 0, i\ne j\end{aligned} \right.$呢？

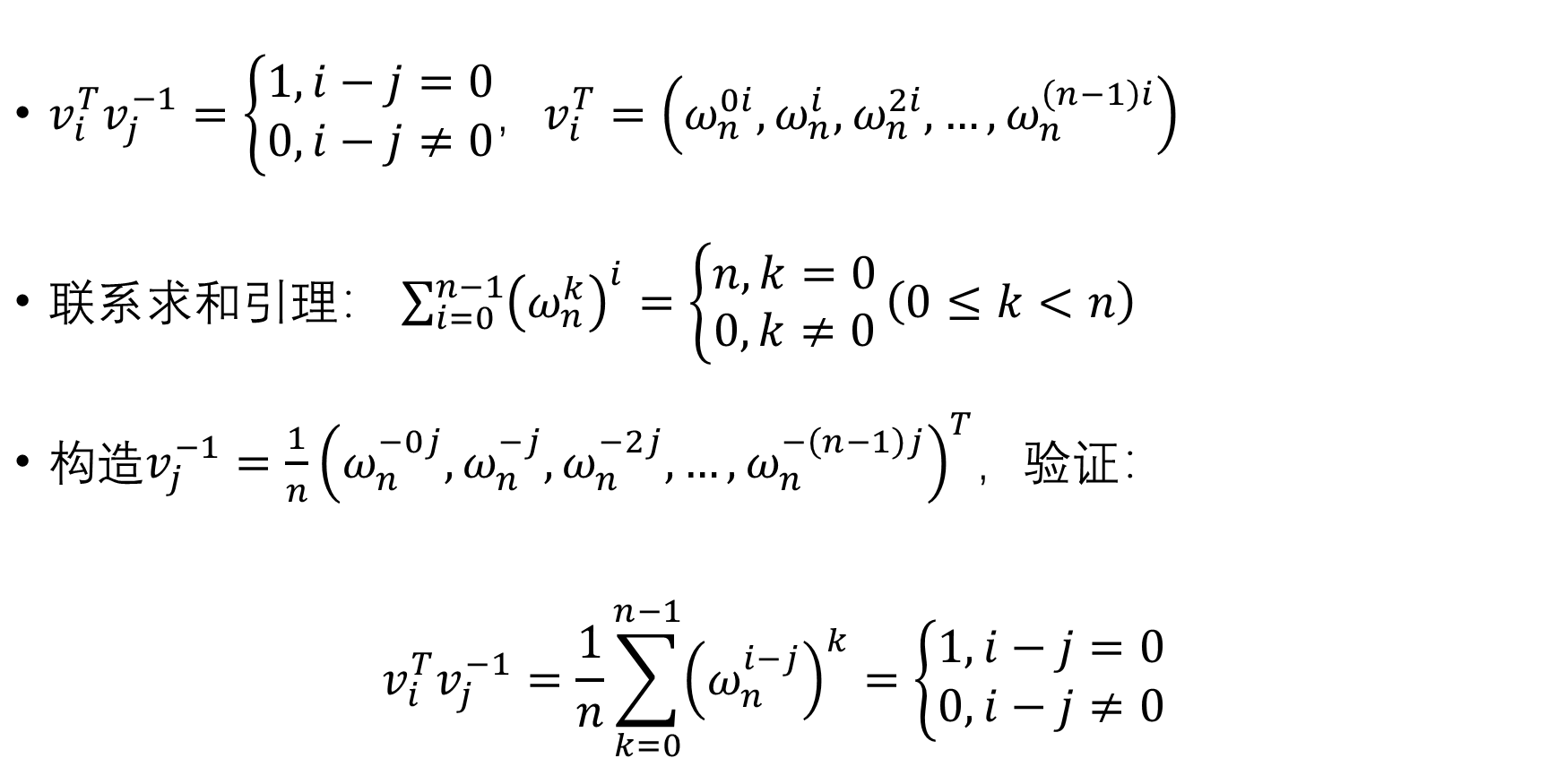
是不是很神？这样我们就构造出了$V^{-1}$：

现在，问题就变成了用$\omega_n^{-1}$为本原单位根，对y向量作FFT以后除以n。PPT里说的吼啊，稍微修改一下代码就行了。

递归实现FFT

#include <cmath>

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int maxn=2e6+5;

const double Pi=3.1415926535898;

int t, n, m, len=1;

struct Cpx{  //复数

    double x, y;

    Cpx (double t1=0, double t2=0){ x=t1, y=t2; }

}A[maxn*2], B[maxn*2], C[maxn*2];

Cpx operator +(Cpx a, Cpx b){ return Cpx(a.x+b.x, a.y+b.y); }

Cpx operator -(Cpx a, Cpx b){ return Cpx(a.x-b.x, a.y-b.y); }

Cpx operator *(Cpx a, Cpx b){ return Cpx(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x); }

void fdft(Cpx *a, int n, int flag){  //快速将当前多项式从系数表达转换为点值表达

    if (n==1) return;  //如果只有1项系数为k，唯一的点值就是(w[1,1],k*w[1,1])=(1, k)

    Cpx a1[(n>>1)+1], a2[(n>>1)+1];

    for (int i=0; i<(n>>1); ++i) a1[i]=a[i<<1], a2[i]=a[i<<1|1];

    fdft(a1, n>>1, flag); fdft(a2, n>>1, flag);

    Cpx w1(cos(2*Pi/n), flag*sin(2*Pi/n)), w(1, 0);  //idft用的负根

    for (int i=0; i<(n>>1); ++i, w=w*w1){

        a[i]=a1[i]+w*a2[i];

        a[i+(n>>1)]=a1[i]-w*a2[i];

    }

}

int main(){

    scanf("%d%d", &n, &m); int x;

    for (int i=0; i<=n; ++i) scanf("%lf", &A[i].x);

    for (int i=0; i<=m; ++i) scanf("%lf", &B[i].x);

    while (len<n+m) len<<=1;  //idft需要至少l1+l2个点值

    fdft(A, len, 1); fdft(B, len, 1);

    for (int i=0; i<len; ++i) C[i]=A[i]*B[i];

    fdft(C, len, -1);  //idft

    for (int i=0; i<=n+m; ++i){

        x=C[i].x/len+0.5;

        printf("%d ", x);

    }

    return 0;

}

题目是luogu的模板。注意给出的n和m都是多项式的最高次数，也就是说乘起来后的多项式最高次数为n+m，至少需要n+m个点。

迭代版FFT

递归版的太慢了，暗中观察我们是如何处理序列的，可以发现：

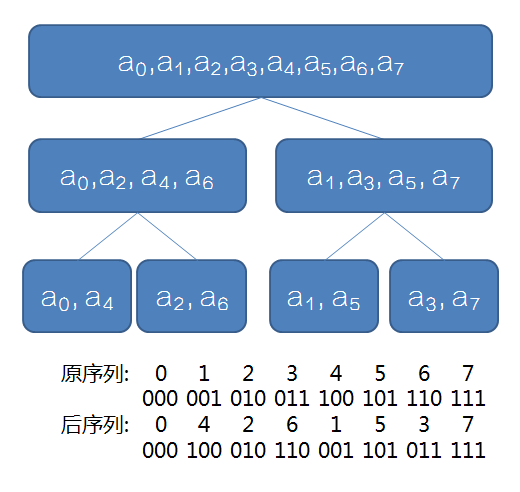
把每个元素的编号二进制反转一下，就是我们要求的序列编号！原因是原序列的最后1位决定了当前元素被分到前半区还是后半区，也就是转换后元素编号的第1位。依次类推。

有一个O(n)推出n个数各自编号镜像反转的方法，大体思想是通过i<<1的反转推出i的反转。

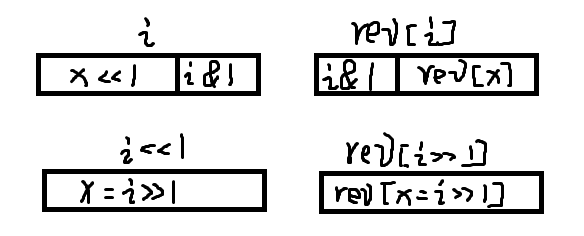
由于各种原因，迭代版要比递归版快四倍左右～

#include <cmath>

#include <cctype>

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int maxn=2e6+5;

const double pi=3.1415926535898;

int t, n, m, len=1, l, r[maxn*2];

struct Cpx{  //复数

    double x, y;

    Cpx (double t1=0, double t2=0){ x=t1, y=t2; }

}A[maxn*2], B[maxn*2], C[maxn*2];

Cpx operator +(Cpx a, Cpx b){ return Cpx(a.x+b.x, a.y+b.y); }

Cpx operator -(Cpx a, Cpx b){ return Cpx(a.x-b.x, a.y-b.y); }

Cpx operator *(Cpx a, Cpx b){ return Cpx(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x); }

void fdft(Cpx *a, int n, int flag){  //快速将当前多项式从系数表达转换为点值表达

    for (int i=0; i<n; ++i) if (i<r[i]) swap(a[i], a[r[i]]);

    for (int mid=1; mid<n; mid<<=1){  //当前区间长度的一半

        Cpx w1(cos(pi/mid), flag*sin(pi/mid)), x, y;

        for (int j=0; j<n; j+=(mid<<1)){  //j:区间起始点

            Cpx w(1, 0);

            for (int k=0; k<mid; ++k, w=w*w1){  //系数转点值

                x=a[j+k], y=w*a[j+mid+k];

                a[j+k]=x+y; a[j+mid+k]=x-y;

            }

        }

    }

}

inline int getint(int &x){

    char c; int flag=0;

    for (c=getchar(); !isdigit(c); c=getchar())

        if (c=='-') flag=1;

    for (x=c-48; c=getchar(), isdigit(c);)

        x=(x<<3)+(x<<1)+c-48;

    return flag?x:-x;

}

int main(){

    getint(n); getint(m); int x;

    for (int i=0; i<=n; ++i) getint(x), A[i].x=x;

    for (int i=0; i<=m; ++i) getint(x), B[i].x=x;

    while (len<=n+m) len<<=1, ++l;  //idft需要至少l1+l2个点值

    for (int i=0; i<len; ++i)  //编号的字节长度为l

        r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));

    fdft(A, len, 1); fdft(B, len, 1);

    for (int i=0; i<len; ++i) C[i]=A[i]*B[i];

    fdft(C, len, -1);  //idft

    for (int i=0; i<=n+m; ++i) printf("%d ", int(C[i].x/len+0.5));

    return 0;

}

这样可以做到1e6的数据最差也能跑进1s。我太菜了，并不会什么常数优化。

两个月后的PS：注意n个点确定一个n-1次多项式。这是因为，对多项式求点值表达，相当于将一个范德蒙德矩阵乘上系数矩阵（前文有图）。而范德蒙德矩阵是可逆的，所以在已知y的情况下，a也是唯一确定的。因此n个点一定唯一确定一个n-1次多项式。

五个月后的PS：qwq 借用了不少大佬的东西，侵删。