Reproducing kernel Hilbert space Mapping the points to a higher dimensional feature space

http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/lecture4_introToRKHS.pdf

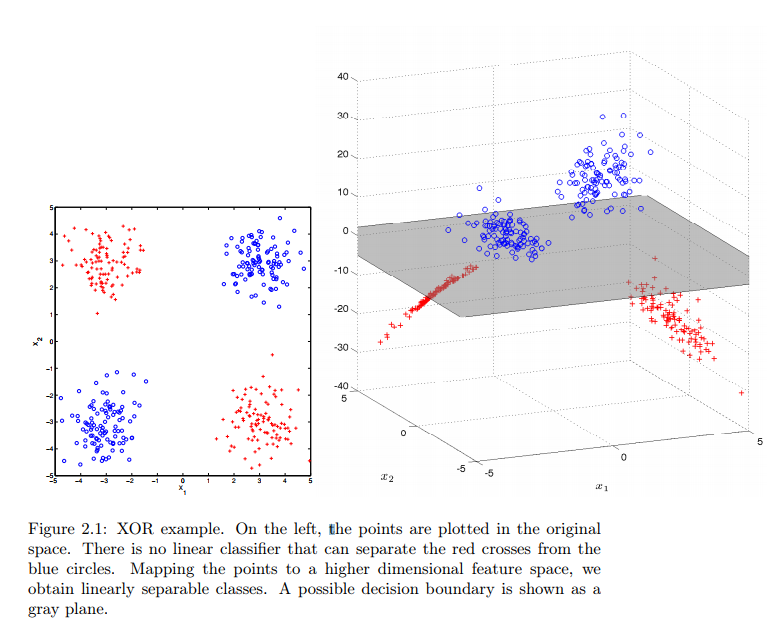
【We next show that every reproducing kernel Hilbert space has a unique positive definite kernel, and vice-versa: this is the Moore-Aronszajn theorem.】

每个可繁殖核希尔伯特空间有一个唯一的正定的核。

Every positive definite kernel k is associated with a unique RKHS H.

We have introduced the notation of feature spaces, and kernels on these feature spaces. What’s more, we’ve determined that these kernels are positive definite. In this section, we use these kernels to define functions on X . The space of such functions is known as a reproducing kernel Hilbert space.

【函数空间-RKHS】

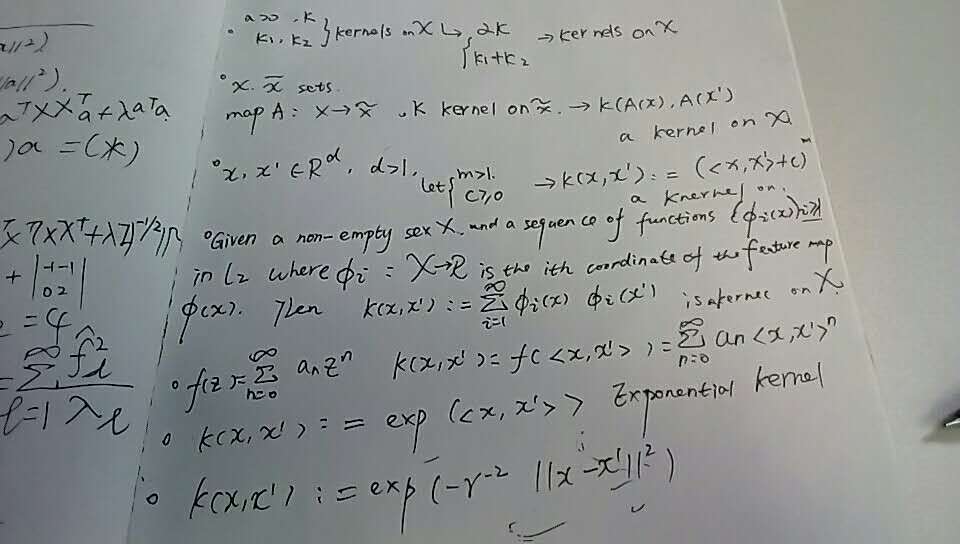
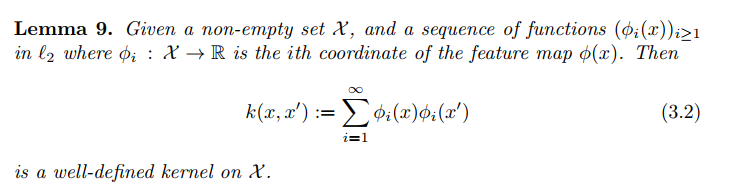
The space of such functions is known as a reproducing kernel Hilbert space.的更多相关文章

  1. paper 10：支持向量机系列七：Kernel II —— 核方法的一些理论补充，关于 Reproducing Kernel Hilbert Space 和 Representer Theorem 的简介。

    在之前我们介绍了如何用 Kernel 方法来将线性 SVM 进行推广以使其能够处理非线性的情况,那里用到的方法就是通过一个非线性映射 ϕ(⋅) 将原始数据进行映射,使得原来的非线性问题在映射之后的空间 ...

  2. Reproducing Kernel Hilbert Space (RKHS)

    目录 概 主要内容 RKHS-wiki 概 这里对RKHS做一个简单的整理, 之前的理解错得有点离谱了. 主要内容 首先要说明的是, RKHS也是指一种Hilbert空间, 只是其有特殊的性质. Hi ...

  3. Cauchy sequence Hilbert space 希尔波特空间的柯西序列

    http://mathworld.wolfram.com/HilbertSpace.html A Hilbert space is a vector space  with an inner prod ...

  4. Hilbert space

    Definition A Hilbert space H is a real or complex inner product space that is also a complete metric ...

  5. 希尔伯特空间（Hilbert Space）是什么？

    希尔伯特空间是老希在解决无穷维线性方程组时提出的概念, 原来的线性代数理论都是基于有限维欧几里得空间的, 无法适用, 这迫使老希去思考无穷维欧几里得空间, 也就是无穷序列空间的性质. 大家知道, 在一 ...

  6. 希尔伯特空间（Hilbert Space）

    欧氏空间 → 线性空间 + 内积 ⇒ 内积空间(元素的长度,元素的夹角和正交) 内积空间 + 完备性 ⇒ 希尔伯特空间 0. 欧几里得空间 欧氏空间是一个特别的度量空间,它使得我们能够对其的拓扑性质, ...

  7. Are Loss Functions All the Same?

    目录 概 主要内容 一些假设 损失函数 损失函数的统计性质 收敛速度 分类的界 Rosasco L, De Vito E, Caponnetto A, et al. Are loss function ...

  8. Kernel methods on spike train space for neuroscience: a tutorial

    郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布! 时序点过程:http://www.tensorinfinity.com/paper_154.html Abstract 在过去的十年中,人 ...

  9. Deep Learning and Shallow Learning

    Deep Learning and Shallow Learning 由于 Deep Learning 现在如火如荼的势头,在各种领域逐渐占据 state-of-the-art 的地位,上个学期在一门 ...

随机推荐

  1. 【Hadoop】Hadoop MR 自定义序列化类

    1.基本概念 2.Mapper代码 package com.ares.hadoop.mr.flowsum; import java.io.IOException; import org.apache. ...

  2. android-SQLite数据库MVC关联实例源码（三层架构）

    前两天布置下了一个期末练习,其中的重点是两个表之间的SQLite关联操作. 拿到题目,首先需要建库和关联表,下面是代码. 我使用简单的表插入,将数据的提交卸载onCreate方法中,这样不会发生写在主 ...

  3. Oracle基础 程序包

    一.程序包 程序包是一种数据库对象,它是对相关PLSQL类型.子程序.游标.异常.变量和常量的封装.程序包包含两部分内容: 1.程序包规范:可以声明类型.变量.常量.异常.游标和子程序. 2.程序包主 ...

  4. scrollTop clientTop offsetTop scrollHeight clientHeight clientWidth的差别及使用方法

    这几个属性做滚动时会经经常使用到.现总例如以下: 首先定义一个div.样式例如以下: <style> *{ margin:0px; padding:0px;} body{ margin:0 ...

  5. 【LeetCode】LeetCode——第14题：Longest Common Prefix

    14. Longest Common Prefix My Submissions Question Editorial Solution Total Accepted: 97052 Total Sub ...

  6. .net 定时服务

    namespace MvcApplication1 { public class MvcApplication : System.Web.HttpApplication { protected voi ...

  7. 高抛低吸T+0操作要领（目前行情短线炒作的必备技能）

    最近的行情只能用操蛋来形容,但是危机中不乏机会.现在已经不是之前行情的思路,那着一个股票长线抱着,即使是好的牛股,也经不起目前行情的这 么折腾.所以,现在最适合的操作方式就是高抛低吸.今天低吸保不准明 ...

  8. GLSL经典新手教程汇总

    权威官方文档:https://www.opengl.org/documentation/glsl/ 权威民间金典新手教程:http://blog.csdn.net/racehorse 一个具体完整的G ...

  9. Struts2 后台获取路径的几种方法

    Struts2 后台获取路径的几种方法 package actions.app; import java.io.File; import org.apache.struts2.ServletActio ...

  10. macOS10.12部署sonarqube5.6.3

    所需安装包已全部上传云盘:https://pan.baidu.com/s/1i5LvOCd 密码:s47e 1. 安装mysql 下载云盘的dmg包,一路默认安装,注意:一定要记住最后一步弹出的默认密 ...