数据结构学习-AVL平衡树

环境：C++ 11 + win10

IDE：Clion 2018.3

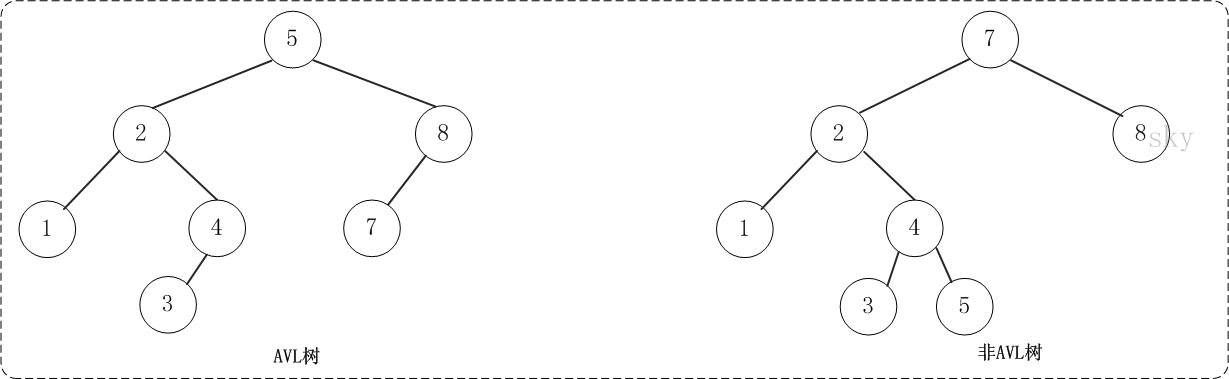
AVL平衡树是在BST二叉查找树的基础上添加了平衡机制。

我们把平衡的BST认为是任一节点的左子树和右子树的高度差为-1,0,1中的一种情况，即不存在相差两层及以上。

所谓平衡机制就是BST在理想情况下搜索复杂度是o(logn)

但是如果在（存在某一节点，该节点的左子树的高度与右子树的高度差>1）这种状况下，复杂度会超过o(logn)

举个极端的例子如加入1,2,3,4，BST就退化为一个线性的链表，复杂度变成了o(n)

为了避免这种情况，我们在BST中引入平衡操作（旋转操作），使得BST始终不存在左右子树超过1高度差的节点。

本次代码基于我的另一篇博客的基础之上，有需要可以翻看 https://www.cnblogs.com/cyrio/p/10118132.html

平衡机制主要通过反转完成，经过归纳，可能出现以下四种不平衡的情况：LL、LR、RL、RR

L=left     R=right

我们将不平衡点设为X点，以LR为例，第一个L表示X点的左子树比右子树层数多（>1），第二个R表示多出的那部分在X点的左子树的右子树。（不管他是在X的左子树的右子树的左右哪边，都称为LR）

如图：

接下来我们以LL、LR、RR、RL四种情况讨论。

1、LL：

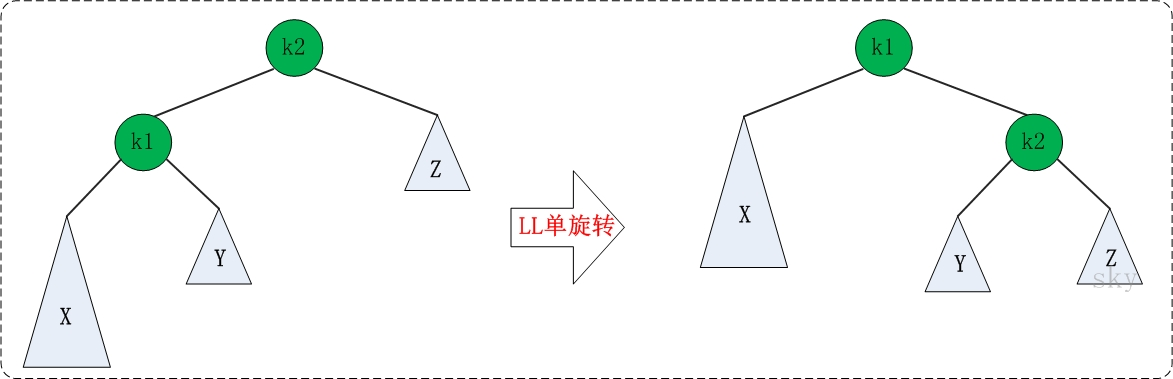
通俗的讲就是把K2从K1那扯下来，然后把Y移到K2的左子树，最后把K2移到K1的右子树。

2、RR：

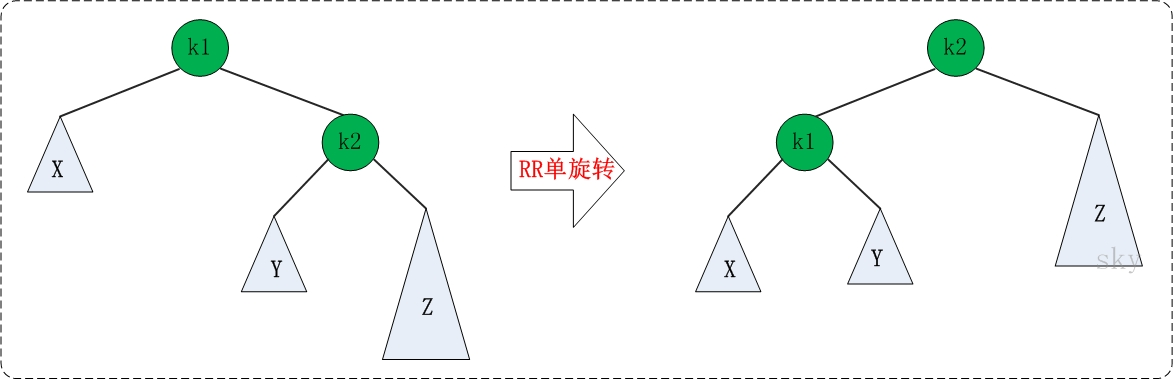
与LL同理，把K1先扯下来，再把Y接到K1的右侧，再把K1作为左子树接到K2。

3、LR：

LR需要先做一次RR再做一次LL：

先把K1从K2那扯下来，让K2和K3连，然后把B作为K1的右子树，再把K1连到K2的左子树上。

然后再做LL，把K3从K2上面扯下来，让C作为K3的左子树，再把K3连到K2的右子树。

4、RL：

先LL再RR，与LR同理。

以上是主要思想的分析，除了旋转操作，我们还需要添加新的方法：

1、求树的高度：height方法

2、求某节点的左子树和右子树的高度差 ：Diff方法

3、一个对整个树进行判断，对里面的X节点进行对应操作：Balance方法

同时AVL中的Insert（插入某一节点）的方法与BST中也略有不同，需要注意的是AVL种的__Insert（PS：带"__"的表示私有内部接口）的参数中第一个为bstNode<T> * & root （需要&引用）

具体代码如下：（此代码为完整代码，可以直接复制进自己的项目查看效果）

myBST.h

#ifndef TEST1_MYBST_H
#define TEST1_MYBST_H

#include <iomanip>
#include "bstNode.h"
#include <vector>
#include <deque>
#include <iostream>
#include <algorithm>
using namespace std;

template <typename T>
class myBST{
private:
    bstNode<T> * root = nullptr;
    bstNode<T> * __search(bstNode<T> * root , const T &key){
        if (nullptr == root)
            return nullptr;
        if (key == root->data)
            return root;
        else if (key < root->data)
            return __search(root->left, key);
        else
            return __search(root->right, key);
    } //查找关键字是否存在
    bstNode<T> * __treeMin(bstNode<T> * root , bstNode<T> * &parent){
        bstNode<T> * curr = root;
        while(curr->left!= nullptr){
            parent = curr;
            curr = curr->left;
        }
        return  curr;
    } //返回最小节点（一路向左）
    bstNode<T> * __Insert(bstNode<T> * &root, const T &key){
        if (nullptr == root)
        {
            root = new bstNode<T>(key);
            return root;
        }//递归返回条件
        else if (key < root->data)
        {
            root->left = __Insert(root->left,key);//递归左子树
            //balance operation
            root = __Balance(root);//平衡操作包含了四种旋转
        }
        else if (key>root->data)
        {
            root->right = __Insert(root->right,key);//递归右子树
            //balance operation
            root = __Balance(root);//平衡操作包含了四种旋转
        }
        return root;
    } //插入指定值
    bool __Delete(const T &key){
        bool found = false;//存储有没有找到key的变量
        if(isEmpty()){
            cerr<<"BST为空"<<endl;
            return false;
        }
        bstNode<T> * curr = root;
        bstNode<T> * parrent = nullptr;
        while(curr!= nullptr) {
            if (key == curr->data) {
                found = true;
                break;
            } else {
                parrent = curr;
                if (key < curr->data) curr = curr->left;
                else curr = curr->right;
            }
        }
        if(!found){
            cerr<<"未找到key！"<<endl;
            return false;
        }
        if (parrent == nullptr){//删除根节点
            root = nullptr;
            delete(curr);
            return true;
        }
        /*
         删除的节点有三种可能：
         1、叶子结点
         2、一个孩子的节点
         3、两个孩子的节点
         */
        if (__isLeaf(curr)){ //删除的点是叶子结点
            if(parrent->left==curr) parrent->left= nullptr;
            else parrent->right= nullptr;
            delete(curr);
            return true;
        }
        else if(__isNodeWithTwoChild(curr)){ //是两个孩子的节点
            //以当前右子树中的最小值取代他
            bstNode<T> * parrent = curr;
            bstNode<T> * tmp = __treeMin(curr->right,parrent);
            curr->data = tmp->data;
            if(parrent->right==tmp)
                parrent->right== nullptr;
            else parrent->left== nullptr;
            delete(tmp);
            return true;
        }
        else{ //只有一个孩子的节点
            if(curr->left!= nullptr){
                if(curr->left == curr){
                    parrent->left=curr->left;
                    delete(curr);
                    return true;
                }
                else{
                    parrent->right=curr->right;
                    delete(curr);
                    return true;
                }
            }
            if(curr->right!= nullptr){
                if(curr->left == curr){
                    parrent->left=curr->left;
                    delete(curr);
                    return true;
                }
                else{
                    parrent->right=curr->right;
                    delete(curr);
                    return true;
                }
            }
        }
        return false;
    } //删除指定值
    bool __isLeaf(bstNode<T> * const & root){
        if(root->left== nullptr && root->right== nullptr) return true;
        else return false;
    }//判断是否是叶子节点
    bool __isNodeWithTwoChild(bstNode<T> * const & root){
        if(root->left!= nullptr && root->right!= nullptr) return true;
        else return false;
    }//判断是否有两个孩子
    void __InorderTraversal(bstNode<T> *root,std::vector<int>&result){
        if(nullptr == root) return;
        __InorderTraversal(root->left,result);
        cout<<root->data<<" ";
        result.push_back(root->data);
        __InorderTraversal(root->right,result);
    }//中序遍历
    void __PreorderTraversal(bstNode<T> *root,std::vector<int>&result){
        if(nullptr == root) return;
        cout<<root->data<<" ";
        result.push_back(root->data);
        __InorderTraversal(root->left,result);
        __InorderTraversal(root->right,result);
    }//前序遍历
    void __PostorderTraversal(bstNode<T> *root,std::vector<int>&result){
        if(nullptr == root) return;
        __InorderTraversal(root->left,result);
        __InorderTraversal(root->right,result);
        cout<<root->data<<" ";
        result.push_back(root->data);
    }//后序遍历
    void __DeleteAllNodes(bstNode<T> *root){
        if (root == nullptr) return;
        __DeleteAllNodes(root->left);
        __DeleteAllNodes(root->right);
        __Delete(root->data);
    }//删除所有节点
    void __BFTraversal(vector<T>&result) {
        deque<bstNode<T> *> TQueue;
        bstNode<T> *pointer = root;
        if (pointer != nullptr) {
            TQueue.push_back(pointer);
        }
        while (!TQueue.empty()) {
            pointer = TQueue.front();
            TQueue.pop_front();
            cout << pointer->data << " ";
            result.push_back(pointer->data);
            if (pointer->left != nullptr) TQueue.push_back(pointer->left);
            if (pointer->right != nullptr) TQueue.push_back(pointer->right);
        }
    } //广度搜索来进行周游
    void __Graph(int indent,bstNode<T>* root){
        if(root != ){
            __Graph(indent + , root->right);
            cout<<setw(indent)<<" "<<root->data<<endl;
            __Graph(indent + , root->left);
        }
    } //横着画图的内部接口
    bstNode<T> * __GetRoot(){
        return root;
    } //返回根节点的内部接口
    //以下为AVL平衡树新加的方法
    int __height(const bstNode<T>* root){
        if(root == nullptr){
            return ;
        }
        return max(__height(root->left),__height(root->right))+;
    } //求树的高度
    int __diff(const bstNode<T>* root){
        return __height(root->left)-__height(root->right);
    } //求节点的高度差（平衡因子）
    bstNode<T> * __ll__Rotation(bstNode<T> * root){
        bstNode<T> * tmp;
        tmp = root->left;
        root->left = tmp->right;
        tmp->right = root;
        return tmp;
    } //单旋转-左左
    bstNode<T> * __rr__Rotation(bstNode<T> * root){
        bstNode<T> * tmp;
        tmp = root->right;
        root->right = tmp->left;
        tmp->left = root;
        return tmp;
    } //单旋转-右右
    bstNode<T> * __lr__Rotation(bstNode<T> * root){
        bstNode<T> * tmp;
        tmp = root->left;
        root->left = __rr__Rotation(tmp);
        return __ll__Rotation(root);
    } //双旋转-左右型，先右后左转（注意此处相反）
    bstNode<T> * __rl__Rotation(bstNode<T> * root){
        bstNode<T> * tmp;
        tmp = root->right;
        root->right = __ll__Rotation(tmp);
        return __rr__Rotation(root);
    } //双旋转-右左型，先左后右转
    bstNode<T> * __Balance(bstNode<T> * root){
        int balanceFactor = __diff(root);//__diff用来计算平衡因子（左右子树高度差）
        if (balanceFactor > )//左子树高于右子树
        {
            if (__diff(root->left) > )//左左外侧
                root=__ll__Rotation(root);
            else//左右内侧
                root=__lr__Rotation(root);
        }
        else if (balanceFactor < -)//右子树高于左子树
        {
            if (__diff(root->right) > )//右左内侧
                root=__rl__Rotation(root);
            else//右右外侧
                root=__rr__Rotation(root);
        }
        return root;
    } //平衡的内部操作
public:
    myBST(){
        root = nullptr;
    } //默认构造
    myBST(vector<T> arr){
        root = nullptr;
        for(int i =;i<(T)arr.size();i++){
            Insert(arr[i]);
        }
    }
    myBST(T * arr,int len){
        root = nullptr;
        for(int i =;i<len;i++){
            __Insert(*(arr+i));
        }
    }
    ~myBST(){
        bstNode<T> * curr = root;
        __DeleteAllNodes(curr);
    }//析构
    bool isEmpty() const{
        return root == nullptr;
    }//判断树空
    bool search(const T &key){
        bstNode<T> * temp = __search(root, key);
        return (temp == nullptr) ? false : true;
    }//查找关键字是否存在的对外接口
    bool Insert(const T &key){
        return __Insert(root,key);
    }//插入节点的外部接口
    bool Delete(const T &key){
        return __Delete(key);
    }//删除节点的外部接口
    void InorderTraversal(vector<T>&result){
        __InorderTraversal(root, result);
    }//中序遍历的外部接口
    void PreorderTraversal(vector<T>&result){
        __PreorderTraversal(root, result);
    }//前序遍历的外部接口
    void PostorderTraversal(vector<T>&result){
        __PostorderTraversal(root, result);
    }//后序遍历的外部接口
    void BFTraversal(vector<T>&result){
        return __BFTraversal(result);
    } //广度搜索外部接口
    void Graph(int indent,bstNode<T>* root){
        return __Graph(indent,root);
    } //横着画图的外部接口
    bstNode<T> * GetRoot(){
        return __GetRoot();
    } //返回根节点的外部接口
};

#endif //TEST1_MYBST_H

bstNode.h

#ifndef TEST1_BSTNODE_H
#define TEST1_BSTNODE_H
template <typename T>
class bstNode{
public:
    T data;
    bstNode* left;
    bstNode* right;
    bstNode(){
        data = ;
        left = nullptr;
        right = nullptr;
    }
    bstNode(T val){
        data = val;
        left = nullptr;
        right = nullptr;
    }
};
#endif //TEST1_BSTNODE_H

main.cpp

#include <iostream>
#include <vector>
#include "myBST.h"
#include "bstNode.h"
using namespace std;
int main() {
    vector<int> in = {,,,,,,,,,};
    myBST<int> bst(in);
    bst.Delete();
    bst.Insert();
    bool found = bst.search();
    if(!found)
        cout<<"not found!"<<endl;
    else
        cout<<"found!"<<endl;
    vector<int> result;
    cout<<"InorderTravelsal:  ";
    bst.InorderTraversal(result);
    cout<<endl<<"PreorderTravelsal:  ";
    bst.PreorderTraversal(result);
    cout<<endl<<"PostorderTraversal:  ";
    bst.PostorderTraversal(result);
    cout<<endl<<"BFTraversal:  ";
    bst.BFTraversal(result);
    cout<<endl<<"Graph:"<<endl;
    bstNode<int>* pointer = bst.GetRoot();
    bst.Graph(,pointer);
    return ;
}

参考：https://blog.csdn.net/zhangxiao93/article/details/51459743