1.什么是NoSql?

2.为什么需要NoSQL？

　　互联网经历了1.0和2.0的发展；

　　web1.0 是早期新浪，雅虎等只能浏览，不能交互；

　　传统关系型数据库在应付web2.0这种动态网站的时候力不从心，暴露出很多难以克服的问题。

　　2.1高并发读写问题

　　　　数据库的承载能力就达不到要求了，每秒上万次的读写；

　　　　读可以，那写也承受不住；

　　　　网站实时统计数的改变，记录热门事件的点击次数，都是写入数据库

　　2.2海量数据的高效率存储和访问

　　　　对于关系型数据库来说，在一张上亿数据的表里进行查询效率是非常低的；

　　　　再比如大型的web网站用户登录系统，也无法高效率的进行访问

　　2.3高可扩展性和高可用性

　　　　在基于web的架构中，数据库是最难进行横向扩展，当一个应用用户数量和访问量与日俱增的时候，

　　　　需要向服务器通过更多的硬件来搭载负载均衡的服务器，对于24小时访问不间断服务的网站来说，

　　　　数据库扩展和升级是需要停机维护和数据迁移；

　　NoSQL解决大规模数据库集中，并且数据种类不同的问题，尤其是大数据应用的难题；

3.NoSQL的产品

　　　　

4.NoSQL的存储类型　

　　

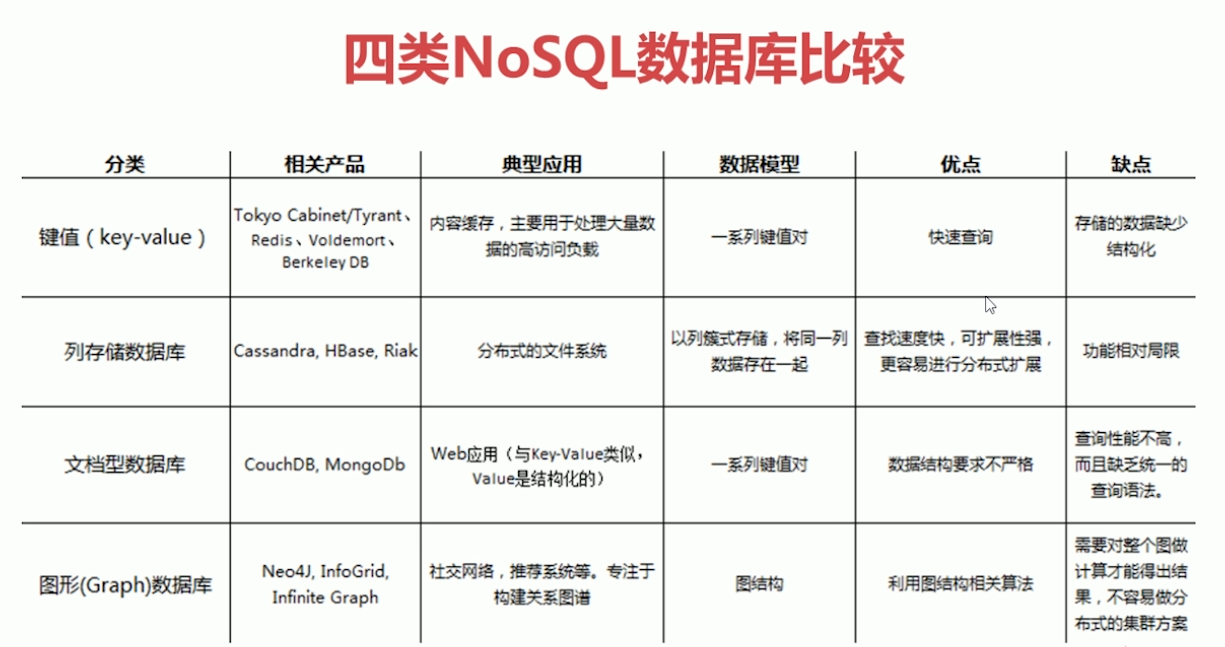
5.NoSQL的特点

　　易扩展

　　灵活的数据模型

　　大量数据的存储，非常高的读写性能

　　不太影响性能的情况下

　　

Redis入门--（一）简介NoSQL的更多相关文章

  1. Redis入门很简单之一【简介与环境搭建】

    Redis入门很简单之一[简介与环境搭建] 博客分类: NoSQL/Redis/MongoDB redisnosqlmemcached缓存中间件  [Redis简介] <一>. NoSQL ...

  2. Redis入门指南之一（简介）

    1. 简介 Redis是一个开源的.高性能的.基于键值对的缓存与存储系统,通过提供多种键值数据类型来适应不同的场景下的缓存与存储需求.同时Redis的诸多高级功能使其可以胜任消息队列.任务队列等不同的 ...

  3. NoSQL之Redis入门笔记

    Redis 1.Redis介绍 1.1 NoSQL:一类新出现的数据库(not only sql),它的特点 不支持sql语法 存储结构跟传统关系型数据库中的那种关系表完全不同,nosql中存储的数据 ...

  4. Redis入门（一）-Redis简介

    最近几年,Rddis非常的火,受到广大中大型公司,特别是互联网公司的青睐.而作为后端开发,如果你不知道Redis或不会用,没用过,你都不好意思出去找工作.可想而知Redis对于IT行业意义多么重大.对 ...

  5. Redis入门及主从配置

    1.Redis入门简介 Redis是一个开源的使用ANSI C语音编写.支持网络.可基于内存亦可持久化的日志型,Key-Value数据库.支持存储的value类型包括 string(字符串).list ...

  6. Redis入门，对Redis的理解和基本环境搭建及操作

    Redis入门使用 参考:https://blog.csdn.net/hellozpc/article/details/81267030 一).缓存的用途举例 1.前端页面广告的数据无需每次查询后台系 ...

  7. Redis入门--进阶详解

    Redis NoSql入门和概述 入门概述 互联网时代背景下大机遇,为什么用nosql 1.单机MySQL的美好年代 在90年代,一个网站的访问量一般都不大,用单个数据库完全可以轻松应付,在那个时候, ...

  8. Redis 入门权威指北

    前言 看看业务遇到了什么问题? 我们要从互联网架构的演变之路开始说起Redis的前世今生. 在我们小的时候,网络世界好像就是只有通过大屁股台式机才能进入一样,彼时的手机只是用来打打电话,发发短信,网上 ...

  9. redis入门笔记(1)

    redis入门笔记(1) 1. Redis 简介 •Redis是一款开源的.高性能的键-值存储(key-value store).它常被称作是一款数据结构服务器(data structure serv ...

  10. Redis入门指南

    随着互联网业务对性能需求日益强烈,作为Key/Value存储的Redis具有数据类型丰富和性能表现优异的特点.如果能够熟练地驾驭它,不管是把它用做缓存还是存储,对很多大型应用都很多帮助.新浪作为世界上 ...

随机推荐

  1. Java框架之Java Bean

    链接 知乎https://www.zhihu.com/question/19773379 总结 符合一定规范的编写的Java类,不是一种技术,而是一种规范.大家对于这种规范,总结了很多开发技巧,工具函 ...

  2. winform按钮文字换行

    用button的Bounds属性 btn.Bounds = new Rectangle(new Point(5 + i * 143, 25), new Size(100, 60));

  3. SAP ABAP ALV构建动态输出列与构建动态内表(包留备用)，包含操作abap元类型表及类

    https://blog.csdn.net/zhongguomao/article/details/51095946

  4. luogu3911 最小公倍数之和(莫比乌斯反演)

    link 给定\(A_1,A_2,\dots,A_N\),求\(\sum_{i=1}^N\sum_{j=1}^Nlcm(A_i,A_j)\) \(1\le N\le 50000;1\le A_i\le ...

  5. 2017第八届蓝桥杯决赛（C++ B组）2.磁砖样式

    磁砖样式 小明家的一面装饰墙原来是 310 的小方格. 现在手头有一批刚好能盖住2个小方格的长方形瓷砖. 瓷砖只有两种颜色:黄色和橙色. 小明想知道,对于这么简陋的原料,可以贴出多少种不同的花样来. ...

  6. ArcGIS Engine 添加SDE数据库

    public void AddSDELayer(bool ChkSdeLinkModle){  //定义一个属性   IPropertySet propset = new PropertySetCla ...

  7. 分页插件PageHelper

    一.PageHelper说明 如果你也在用Mybatis,建议尝试该分页插件,这个一定是最方便使用的分页插件. 该插件目前支持Oracle,Mysql,MariaDB,SQLite,Hsqldb,Po ...

  8. C语言文件I/O和标准I/O函数

    读取/写入  相对于文件而言 输入/输出 相对于程序/内存而言 一切皆文件,键盘.显示屏也是文件,只不过是特殊的标准文件: 标准文件:标准输入.标准输出.标准错误:---->对应的文件指针:st ...

  9. 何为 “元组”（Tuple）？

    元组是关系数据库中的基本概念,关系是一张表,表中的每行(即数据库中的每条记录)就是一个元组,每列就是一个属性.  在二维表里,元组也称为记录.

  10. POJ3368

    http://poj.org/problem?id=3368 给出一个升序数组和 q 个查询.对每个查询,返回 a b 之间出现次数最多的那个元素的出现次数. 这一类区间查询的问题很容易想到用线段树来 ...