面向对象设计与构造：JML规格单元作业总结

面向对象设计与构造：JML规格单元作业总结

第一部分：JML语言理论基础

---

JML语言是什么：对Java程序进行规格化设计的一种表示语言

使用JML语言有什么好处：

• 用逻辑严格的规格取代自然语言，照顾马龙的语文水平。一切挑战规则的行为必将受到严厉惩罚
• 代码维护性高，让大牛的代码不再晦涩，让轮子制造机无机可乘

JML(Level 0)语法

• 单行注释

//@ public model non_null int [] elemen![]ts;

JML规格所管理的数据(规格变量)，并非类的组成部分，non_null指数组对象引用不能为NULL

//@public static model non_null int []elements； //静态规格变量

//@public instance model non_null int []elements； //实例规格变量

一个类型的成员要么是静态成员(static member)，要么是实例成员(instance member)。一个类的静态方法不可以访问这个类的非静态成员变量（即实例变量）。静态成员可以直接通过类型来引用，而实例成员只能通过类型的实例化对象来引用。因此，在设计和表示类型规格时需要加以区分。

public abstract /@ pure @/ int largest(); //pure方法为存粹方法，执行不产生副作用:不会对对象的状态进行任何改变，也不需要提供输入参数，这样的方法无需描述前置条件，也不会有任何副作用，且执行一定会正常结束

• 块注释

/@ public normal_behavior

@ requires elements.length >= 1; //前置条件(precondition)

@ assignable \nothing; //副作用范围限定，为nothing表示此方法为pure方法

@ ensures ...; //后置条件(postcondition)

@/

• 原子表达式

\result ： 方法执行后的返回值，\result表达式的类型就是方法声明中定义的返回值类型

\old(expr) ：表示一个表达式expr在相应方法执行前的取值

• 量化表达式

(\forall int i,j; exprA ; exprB) ; //针对所有满足前置条件exprA的i，j。若都满足exprB，则整个表达式返回true

(\forall int i,j; 0 <= i && i < j && j < 10; a[i] < a[j])；

(\exists int i,j; exprA ; exprB) ; //存在给定范围exprA内的i，j，若存在满足exprB的情况，则整个表达式返回true

(\exists int i; 0 <= i && i < 10; a[i] < 0)

(\sum int i,j; exprA ; exprB) ; //存在给定范围exprA内的i，j，返回表达式exprB的和

(\sum int i; 0 <= i && i < 5; i*i);

(\max int i; exprA ; exprB) ; //存在给定范围exprA内的i，返回表达式exprB的最大值

(\max int i; 0 <= i && i < 5; i)；

(\num_of int x; exprA ; exprB); //存在给定范围exprA内的x，返回满足exprB的取值的个数

(\num_of int x;0<x&&x<=20;x%2==0);

• 操作符

等价关系操作符： b_expr1<==>b_expr2 或者 b_expr1<=!=>b_expr2

推理关系操作符： b_expr1==>b_expr2 或者 b_expr2<==b_expr1

变量引用操作符：\nothing指示一个空集；\everything指示一个全集，经常在assignable句子中使用

• 方法规格

前置条件(pre-condition)：requires P或者requires P1 || P2，方法规格中可以有多个requires子句，是并列关系

后置条件(post-condition)：： ensures P(P1||P2 )，同前置

副作用范围限定(side-effects)：assignable 或者 modifiable，如

private /@spec_public@/ ArrayList elements;

private /@spec_public@/ Integer max;

@assignable elements, max；

@modifiable \nothing

异常：

/@ public normal_behavior

@ 。。。

@ also

@ public exceptional_behavior

@ requires z < 0;

@ assignable \nothing;

@ signals (IllegalArgumentException e) true;

@ also

@ public exceptional_behavior

@ requires z < 0;

@ assignable \nothing;

@ signals_only IllegalArgumentException;

@*/

• 类型规格

  • 不变式invariant：是要求在所有可见状态(凡是会修改成员变量，包括静态成员变量和非静态成员变量的方法执行期间)下都必须满足的特性。可以在不变式定义中明确使用 instance invariant 或 static invariant 表示不变式的类别

  private /@spec_public@/ ArrayList seq_nodes;
  
  private /@spec_public@/ Integer start_node;
  
  private /@spec_public@/ Integer end_node;
  
  /@ invariant seq_nodes != null &&
  
  @ seq_nodes[0] == start_node &&
  
  @ seq_nodes[seq_nodes.legnth-1] == end_node &&
  
  @ seq_nodes.length >=2;
  
  @/

  • 状态变化约束constraint：对象的状态在变化时往往也许满足一些约束，cons对前序可见状态和当前可见状态的
    
    关系进行约束

  private /@spec_public@/ long counter;
  
  //@spec_public@/来注释一个类的私有成员变量，表示在规格中可以直接使用，从而调用者可见。
  
  //@ invariant counter >= 0;
  
  //@ constraint counter == \old(counter)+1;

JML手册：

https://oo-public-1258540306.cos.ap-beijing.myqcloud.com/experiments/experiment_5/JML Level 0手册.pdf

第二部分：应用工具链

---

openJML

​ OpenJML is a program verification tool for Java programs that allows you to check the specifications of programs annotated in the Java Modeling Language.

Github发行版：

https://github.com/OpenJML/OpenJML/releases

OpenJML(IDEA)硬核玩家：

https://course.buaaoo.top/assignment/66/discussion/193

OpenJML基本使用：

https://course.buaaoo.top/assignment/66/discussion/198

给以上两位奆佬递茶～

功能

写在前面：OpenJML不支持\forall int[] 和 \exists int[]等语法。

• JML规格静态检查：判断JML规格的正确性(无关代码)

  下载release，解压得到的几个 jar 包放入 Solvers-windows 文件夹，再把Solvers-windows放在C:\jmlunitng

  该目录下新建JMLcheck.bat和JMLTest.java
  
  JMLcheck.bat：java -jar openjml.jar -check %1
  
  cmd命令：JMLcheck.bat JMLTest.java

  public class JMLTest {
      /*@
        @ public normal_behaviour
        @ requires lhs<0 &&
      */
      public static int compare(int lhs, int rhs) {
          return lhs - rhs;
      }
  
      public static void main(String[] args) {
          compare(114514, 1919810);
      }
  }
  

可以看到规格的第三行Invalid

• 代码静态检查

  java -jar specs openjml.jar -esc XXX.java //找出程序代码潜在错误

  windows命令行下似乎不太友好~

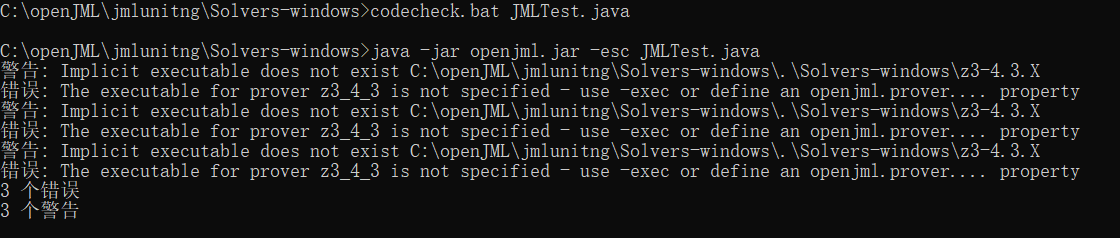
• 动态检查

  java -jar specs openjml.jar -rac XXX.java //运行后生成一个.class文件(该class文件是openJML根据我们的JML规格生成的assertion)，运行该文件即可查看异常或其他信息。(可反编译该文件查看具体内容)

public class JMLTest {
    /*@
      @ public normal_behaviour
      @ requires lhs > 0 && rhs > 0;
    */
    public static int compare(int lhs, int rhs) {
        return lhs - rhs;
    }

    public static void main(String[] args) {
        compare(-45, -5);
    }
}

java -jar openjml.jar -rac JMLTest.java

java -cp .;C:\openJML\jmlunitng\Solvers-windows\jmlruntime.jar JMLTest

对此时的JMLTest.class进行反汇编

网站：

http://www.javadecompilers.com/ (选用CFR)

可看到对应报错的位置JMLTest.java:11

JMLUnitNG

JMLUnitNG is an automated unit test generation tool for JML-annotated Java code

伸手党入口：

https://course.buaaoo.top/assignment/71/discussion/199

功能

根据JML语言生成TestNG测试

SMT Solver

把程序翻译成数学表达式丢给SMT solver来判断正确性

SMT solver简介：

https://zhuanlan.zhihu.com/p/30520308

SMT solver使用：

https://course.buaaoo.top/assignment/66/discussion/189

功能

openjml使用SMT Solver来对检查程序实现是否满足所设计的规格(specification)

部署SMT Solver

---

IDEA + Z3-4.7.1

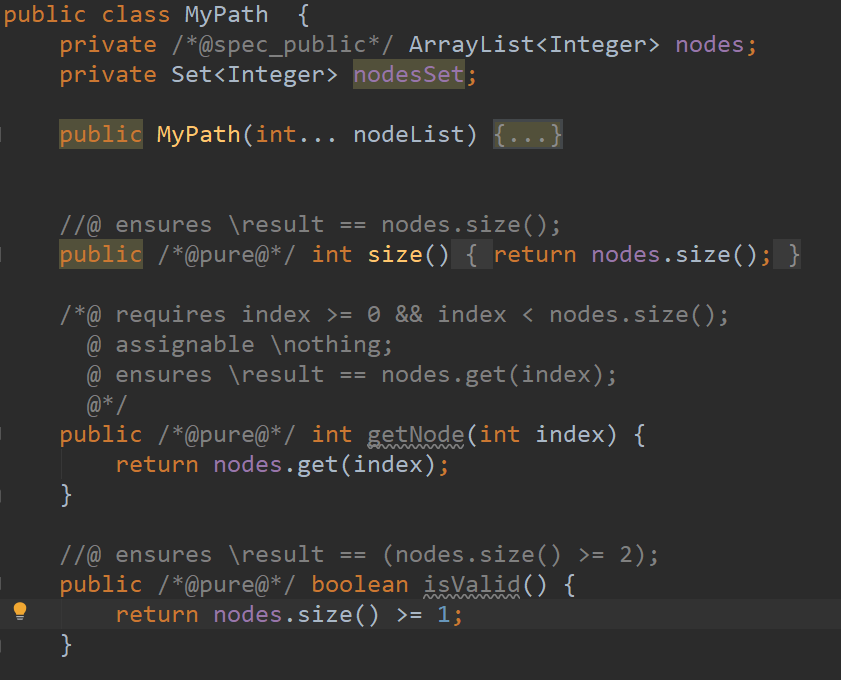
检查报错内容：

可看到isValid方法中，代码与JML规格不符

第三部分：JMLUnitNG

---

测试代码

package JMLTest;

public class JMLTest {
    /*@ public normal_behaviour
      @ ensures \result == lhs - rhs;
    */
    public static int compare(int lhs, int rhs) {
        return lhs - rhs;
    }

    public static void main(String[] args) {
        compare(114514,1919810);
    }
}

java -jar jmlunitng.jar JMLTest\JMLTest.java

java -jar openjml.jar -rac JMLTest/JMLTest.java

javac -cp jmlunitng.jar JMLTest/**.java

java -cp jmlunitng.jar JMLTest\JMLTest

生成的测试样例

[TestNG] Running:
  Command line suite

Passed: racEnabled()
Passed: constructor Demo()
Passed: static compare(-2147483648, -2147483648)
Failed: static compare(0, -2147483648)
Failed: static compare(2147483647, -2147483648)
Passed: static compare(-2147483648, 0)
Passed: static compare(0, 0)
Passed: static compare(2147483647, 0)
Failed: static compare(-2147483648, 2147483647)
Passed: static compare(0, 2147483647)
Passed: static compare(2147483647, 2147483647)
Passed: static main(null)
Passed: static main({})

===============================================
Command line suite
Total tests run: 13, Failures: 3, Skips: 0
===============================================

jmlunitng仅仅使用了整数最大值，最小值以及0进行检查，测试覆盖性较差。

第四部分：架构设计

---

第一次作业

丝路

MyPathContainer

• plist（pidlist）：路径与路径ID之间的映射关系。利于contains，get相关查询操作
• nodeMap：记录结点编号与结点出现次数的映射关系。利于全局distinctNodeCount查询操作
• idCount：全局路径ID增长器
• inputNodeMap，outputNodeMap：更新状态，被add，remove类方法调用，这样做的原因是抽象出状态更新器为后续功能扩展提供上层接口

MyPath

• nodeSet ：结点编号集合。利于containsNode和路径内distinctNodeCount查询操作
• 重写HashCode和equals：为PathContainer容器中的HashMap服务

UML

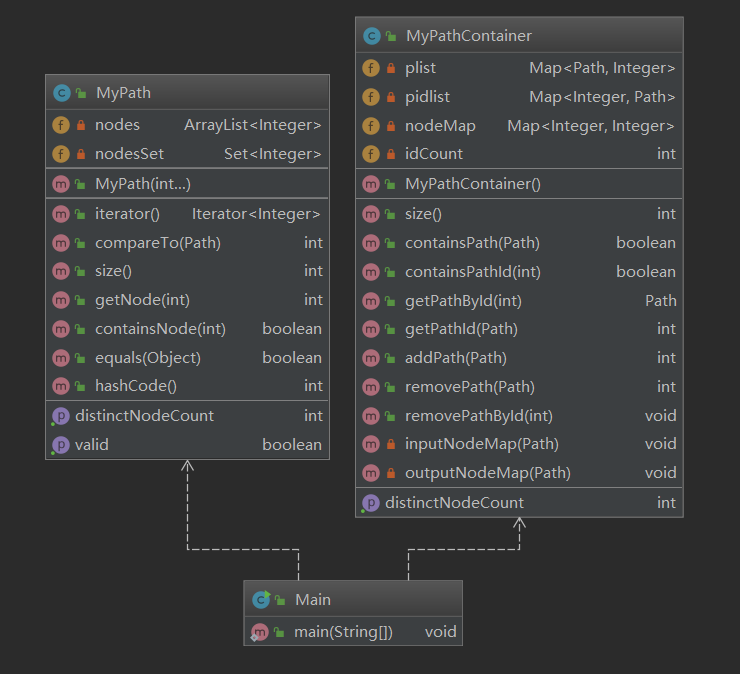
第二次作业

丝路

CalGraph：图计算类

• 静态数组+BFS策略解决最短路
• nodeList，nodeIdList：图内结点实际ID与分配编号映射关系
• availNode，usedNode：记录图内编号分配情况
• graph：邻接表
• graphChanged：本次查询距上一次查询期间是否有增删图操作
• edges：二维矩阵，edges[i][j]记录结点i和j之间所连接的边数
• shortestPath：二维矩阵，最短距离矩阵，可判断两点的连通性

MyGraph，MyPath：基于上次扩展，无重构

UML

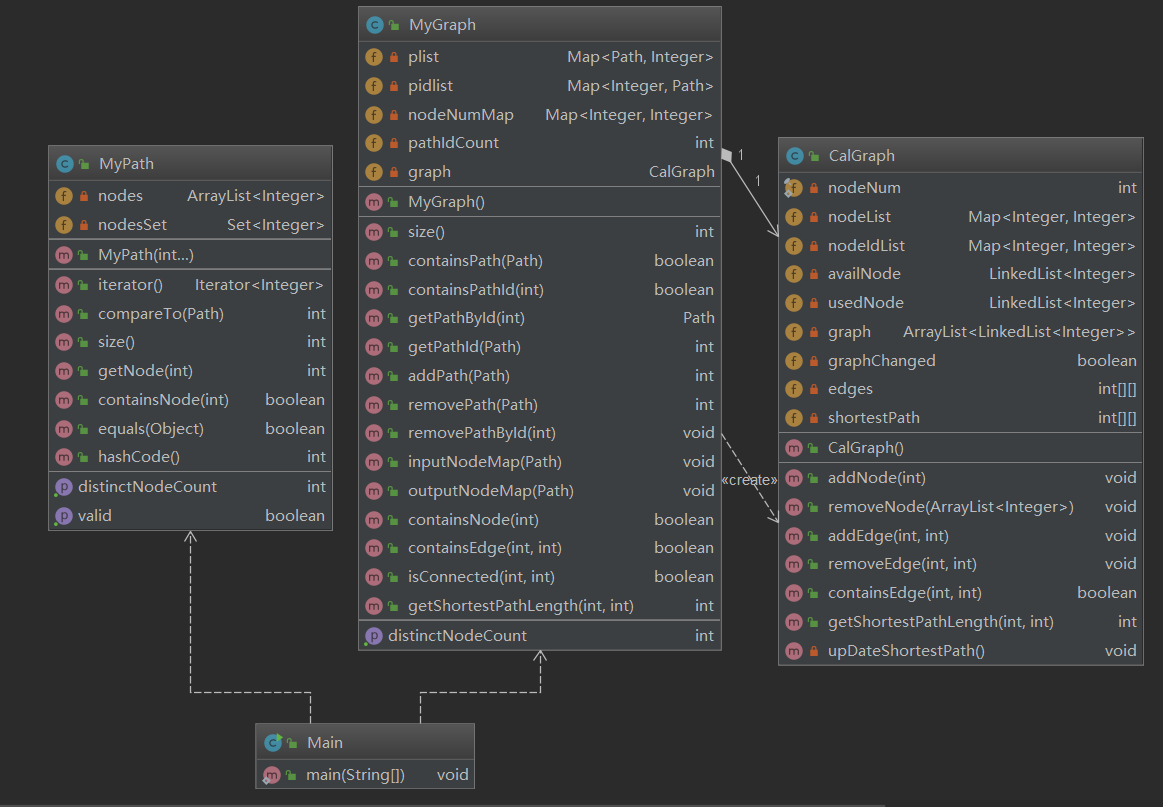
第三次作业

丝路

整体架构

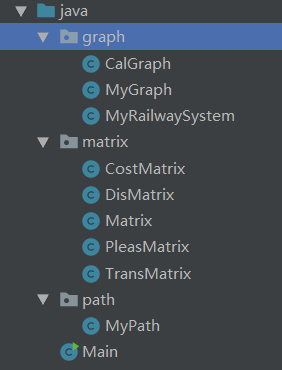
非拆点构图做法(以最小花费为例)

步骤1：为每一条Path构建自身最小花费图

• 0→1→2：直连边的权值为3(基础花费1+换乘花费2)，新添非直连边1→3边权为两结点的最短路+换乘花费2
• 确保Path内任意两点间均有边相连

步骤2：以Path为单位构建整个最小花费图

步骤3：以最短路形式更新整个最小花费图，如图中的0号结点到3号结点新添权值为3+3的边

• 确保整个图内任意两点间均有边

步骤4：最终的最小花费为边权 - 2，如0到5的最小花费为7-2 = 5

简单验证行为正确性

• 当源节点A和换乘结点B在一条Path中，换乘结点B和目的结点C在一条Path中
• 按上述方式在Path内构建最小花费图，设A到B边权t1, B到C边权t2
• A到B的边权为t1 = A到B的最短路+2,在一条路径内无换乘因此A到B开销为t1-2,同理B到C为t2-2
• A到C经历了一次换乘，开销应为A到B最短路+B到C最短路+2，即(t1-2)+(t2-2)+2,即t1+t2-2(A到C边权-2)
• 当源结点A和换乘结点B不在同一条Path中，A到B的边权可以看作上述过程更新后的结果

因此

最短路径：普通构图即可

最少换乘：一个Path内任意两点边权为1+MAX(最大换乘次数)，构建整个换乘最短图后，最少换乘为(边权-MAX)/MAX

最少不满意度：Path内任意两点边权为最少不满意度+32(以最短路形式找两点间的最少不满意度)，构建整个换乘最短图后，最少不满意度为边权-32

算法：当然是Floyed啦~

UML

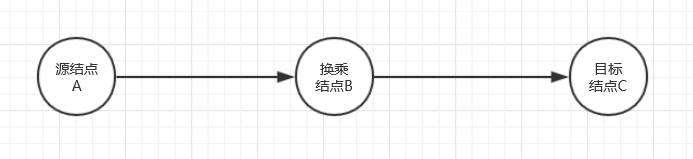
此处只说明一下矩阵类，也是我架构中的精华

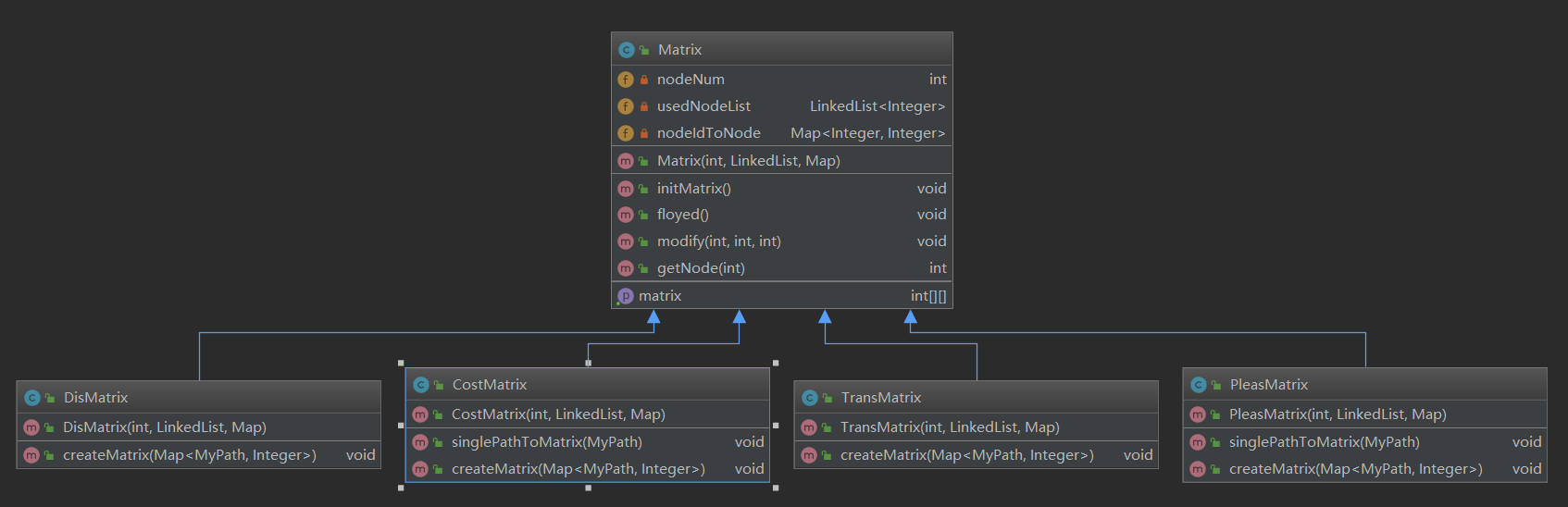
• 几种矩阵的初始化方式相同(ij=MAX_NUM，ii=0)，均需floyed来对图更新，均需修改图中的数据。上述行为被抽象为父类公有方法，结点ID与所分配编号的映射也是所有子类所公有的数据成员。子类的构图方式createMatrix有所不同，因此被抽象为子类特有方法

• nodeNum:数据范围(120或者80)

• usedNodeList：已分配编号的集合(不超过120)，主要是为floyed遍历时剪枝，无需考虑未加入图中的结点

• nodeIdToNode: 结点ID到所分配编号的映射

• matrix: 静态二维数组

• singlePathToMatrix: 满意度矩阵和花费矩阵的特有方法，实际上是为一个Path内构建上述两矩阵提供接口，这一点从createMatrix和singlePathToMatrix的参数类型可以看出。至于为什么要在一个Path类构造上述两种矩阵，其实是为了覆盖更新，例如满意度矩阵的createMatrix方法如下:

  public void createMatrix(Map<MyPath, Integer> pathSet) {
          initMatrix();
          for (MyPath path : pathSet.keySet()) {
              for (int i = 0; i < path.size() - 1; i++) {
                  for (int j = i + 1; j < path.size(); j++) {
                      int sraNode = getNode(path.getNode(i));
                      int dstNode = getNode(path.getNode(j));
                      if (sraNode != dstNode) {
                          int pvalue = path.getShortUnpleasantValue( //从这里可以看出Path内存在
                                  path.getNode(i), path.getNode(j)) + 32; //一个单独的满意度矩阵
                          if (getMatrix()[sraNode][dstNode] > pvalue) {
                              modify(sraNode, dstNode, pvalue);
                              modify(dstNode, sraNode, pvalue);
  ...
  

关于重构

• 在上述Path内新增两种矩阵，意味着MyPath需要新增方法与属性
• 除此之外，需要在Graph类新增自定义方法和规格接口，再增加PathSet一类的管理数据
• 新增Matrix类，为CalGraph类的计算提供合理的组织结构

第五部分：BUG

---

直接上第三次~

被Hack

所有Distinct_Node_Count超过80的数据点均会报错，输出为负值的结果

错位定位

public class Matrix {
    //private static int nodeNum;
    private int nodeNum;
    ...

对你没有看错，注释掉的那一行为提交的版本，下面一行为修复版本。即删掉一个static让我修复了：

16个强测点 + 37个hack点

为什么呢？

public Matrix(int nodeNum, LinkedList usedNodeList, Map nodeIdToNode) {
        this.nodeNum = nodeNum;
    	...
}

​ 这是俺Matrix类的构造方法。static意味着，当第一次创建Matrix时传入的nodeNum参数会初始化该类的静态数据nodeNum，初始化后的静态数据生命周期终结于整个APP结束。然后我，我，，忘了我先创建Path时，在Path内构造了两个Matrix，传入的参数为80，即结点序列的最大长度。

​ 最魔鬼的是，我自己构造的测试单元把数据卡在了40以内。为什么呢？ 因为我认为小数据集验证程序的正确性后，大数据只需保证合理的数据范围即可。当然学习过程中会犯蠢，只希望以后不犯这么蠢的错误就好 ~

Hack别人

C组的生态真是恐怖，某哥们儿的战绩：119/119。我怀疑他在犯罪，但我没有证据

eg.1

样例：

PATH_ADD 0 2 1

LEAST_TICKET_PRICE 1 0 //出错

局内Saber大哥一个类里写了790行代码

public int addPath(Path path) {
    ...
    if (change == 1) {
       getShortestLenth(); }
	...
}

​ 采用和我一样的设计思路，存在的问题是每次addPath就更新图，但是这种设计方法不能把Path独立起来看待。在对于图的更新时，要把所有Path一次性加入一张干净的图中。导致他的程序从架构层面就问题不断。

eg.2

样例：

PATH_ADD 1 1 2

PATH_DISTINCT_NODE_COUNT 1

CONTAINS_PATH_ID 1

CONTAINS_EDGE 1712678435 1336430457

CONNECTED_BLOCK_COUNT

PATH_REMOVE_BY_ID 1

CONNECTED_BLOCK_COUNT //出错

​ Rider的代码风格我很喜欢，出错的原因是样例中第一次CONNECTED_BLOCK_COUNT正确，但removePath后的第二次CONNECTED_BLOCK_COUNT出错。

private void reset() {
        mapping.reset();
        initMat(initMat);
        initMat(unpleasantMat);
        initMat(priceMat);
        for (Path path : paths) {
            addPath(path);
        }
}

​ reset方法是在remove函数中调用的，乍一看没啥毛病。深入addPath后知道没处理好pathId与path对应的问题，以至于remove会出现在某些情况下remove掉错的path。

eg.3

样例：

PATH_ADD 2 0 2 1 1

PATH_ADD 41 10 31 66 3 69 2 53 30 54

PATH_ADD 18 78 65 14 15 75 58 78 50 49

PATH_REMOVE_BY_ID 3

PATH_REMOVE 1 0 2 0 0

LEAST_TRANSFER_COUNT 1 2 //错误

​ Caster还是把MyRailwaySystem写得过于臃肿(刚好卡在500行)，方法实现和接口没有隔离。

public int getLeastTransferCount(int fromNodeId, int toNodeId) throws
  	...
    Eyz con = new Eyz(fromNodeId,toNodeId);
    if (!tran.containsKey(con)) {
        minpath(con,tran,djsttran,trangraph,2);
    }
    return tran.get(con);
}

private void minpath(Eyz eyz, HashMap<Eyz,Integer> queue,
      HashMap<Integer,Minpath> mid,HashMap<Qyz,HashMap<Qyz,Qyz>> graph,int type) {
    if (mid.containsKey(eyz.get(0))) {
        mid.get(eyz.get(0)).count(eyz,queue,type);
    } else {
        Minpath mp = new Minpath(graph,eyz.get(0),type,jcnode);
        mid.put(eyz.get(0),mp);
        mid.get(eyz.get(0)).count(eyz,queue,type);
    }
}

​ 我猜想这里的minpath应该是更新图一类的操作，但说实话我着实看不懂他的命名，也没有代码注释(内心有点小崩溃

出错的原因应该还是没有维护好图。

嗯，还有很多（毕竟，我这次挺