洛谷 P2486 [SDOI2011]染色

题目描述

输入输出格式

输入格式：

输出格式：

对于每个询问操作，输出一行答案。

输入输出样例

输入样例#1：

6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5

输出样例#1：

3
1
2

说明

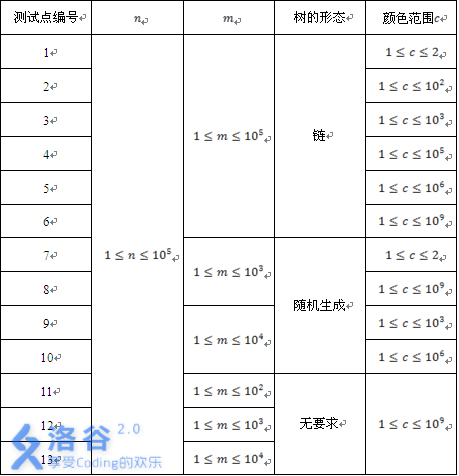
题解：

树剖，用线段树维护：

数组tot[N]表示此时的颜色段数。

数组zzz[N]表示此时最左边的节点的颜色。

数组yyy[N]表示此时最右边的节点的颜色。

则： 首先我们要明确，线段树的叶子节点一定只有一种颜色，也就是一条颜色段。

tot[父亲]=tot[左儿子]+tot[右儿子]；

if (zzz[右儿子]==yyy[左儿子]) {tot[父亲]--;}

即如果右儿子的最左边颜色和左儿子的最右边颜色相同，那么肯定有中间部分属于同一颜色段。

代码：

#include <cstdio>
    #include <cstring>
    #include <iostream>
    #define k (z+y>>1)
    #define ll (r<<1)
    #define rr (r<<1|1)
    using namespace std;
    const int N=1e5+;int a[N];
    int ys[N],s[N*][],o[N],cnt,dfn,n;
    int zzz[N*],yyy[N*],laz[N*],tot[N*];
    int d[N],siz[N],son[N],top[N],f[N],id[N];
    void jia(int a,int b)
    {
        s[++cnt][]=o[a];
        s[cnt][]=b;o[a]=cnt;
        return;
    }
    void shang(int r)
    {
        tot[r]=tot[ll]+tot[rr];
        zzz[r]=zzz[ll];yyy[r]=yyy[rr];
        if (zzz[rr]==yyy[ll]) tot[r]--;
        return;
    }
    void xiangxia(int r,int z,int y)
    {
        tot[ll]=tot[rr]=;
        zzz[ll]=zzz[rr]=yyy[ll]=yyy[rr]=laz[ll]=laz[rr]=laz[r];
        laz[r]=;return;
    }
    void jianshu(int r,int z,int y)
    {
        if (z==y) {
            tot[r]=;zzz[r]=yyy[r]=ys[a[z]];
            return;
        }
        jianshu(ll,z,k);jianshu(rr,k+,y);
        shang(r);return;
    }
    void gai(int r,int z,int y,int zz,int yy,int v)
    {
        if (z==zz&&y==yy) {
            tot[r]=;laz[r]=zzz[r]=yyy[r]=v;
            return;
        }
        if (laz[r]) xiangxia(r,z,y);
        if (zz>k) gai(rr,k+,y,zz,yy,v);
        else if (yy<=k) gai(ll,z,k,zz,yy,v);
        else {gai(ll,z,k,zz,k,v);gai(rr,k+,y,k+,yy,v);}
        shang(r);return;
    }
    int chaxun(int r,int z,int y,int zz,int yy)
    {
        if (z==zz&&y==yy) return tot[r];
        if (laz[r]) xiangxia(r,z,y);
        if (zz>k) chaxun(rr,k+,y,zz,yy);
        else if (yy<=k) chaxun(ll,z,k,zz,yy);
        else {
            int ans=chaxun(ll,z,k,zz,k)+chaxun(rr,k+,y,k+,yy);
            if (zzz[rr]==yyy[ll]) ans--;
            return ans;
        }
    }
    void dfs1(int x,int fa,int dep)
    {
        f[x]=fa;d[x]=dep;siz[x]=;
        for (int i=o[x];i;i=s[i][]) {
            if (s[i][]!=fa) {
                dfs1(s[i][],x,dep+);
                siz[x]+=siz[s[i][]];
                if (siz[s[i][]]>siz[son[x]]) son[x]=s[i][];
            }
        }
        return;
    }
    void dfs2(int x,int tp)
    {
        top[x]=tp;id[x]=++dfn;a[dfn]=x;
        if (son[x]) dfs2(son[x],tp);
        for (int i=o[x];i;i=s[i][])
        if (s[i][]!=f[x]&&son[x]!=s[i][])
        dfs2(s[i][],s[i][]);
        return;
    }
    void ranse(int x,int y,int v)
    {
        while (top[x]!=top[y]) {
            if (d[top[x]]>d[top[y]]) swap(x,y);
            gai(,,n,id[top[y]],id[y],v);
            y=f[top[y]];
        }
        if (d[x]>d[y]) swap(x,y);
        gai(,,n,id[x],id[y],v);
        return;
    }
    int newww(int r,int z,int y,int p)
    {
        if (z==y) return zzz[r];
        if (laz[r]) xiangxia(r,z,y);
        if (p>k) return newww(rr,k+,y,p);
        else return newww(ll,z,k,p);
    }
    int xunwen(int x,int y)
    {
        int ans=,nc,fc;
        while (top[x]!=top[y]) {
            if (d[top[x]]>d[top[y]]) swap(x,y);
            ans+=chaxun(,,n,id[top[y]],id[y]);
            nc=newww(,,n,id[top[y]]);
            fc=newww(,,n,id[f[top[y]]]);
            y=f[top[y]];if (nc==fc) ans--;
        }
        if (d[x]>d[y]) swap(x,y);
        ans+=chaxun(,,n,id[x],id[y]);
        return ans?ans:;
    }
    int main()
    {
        int m,a,b,c;
        cin>>n>>m;char caozuo[];
        for (int i=;i<=n;i++) scanf("%d",&ys[i]);
        for (int i=;i<n;i++) {
            scanf("%d%d",&a,&b);jia(a,b);jia(b,a);
        }
        dfs1(,,);dfs2(,);jianshu(,,n);
        while (m--) {
            scanf("%s",caozuo);
            scanf("%d%d",&a,&b);
            switch (caozuo[]) {
                case 'C':scanf("%d",&c);
                ranse(a,b,c);break;
　　　　　　　　　default:

                printf("%d\n",xunwen(a,b));break;
            }
        }
        //zhu wo zao dian AC!!!
        return ;
    }

ok!!!