卡特兰数&错排&一个一直记不住的公式
卡特兰数
公式:f(x)=f(2)*f(x-1)+f(3)*f(x-2)+......+f(x-1)*f(2)
#include<iostream>
#include<cstdlib>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<ctime>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
using namespace std;
int a[1000];
int main(){
int n,m,i,j,k;
cin>>n;
a[2]=a[3]=1;
a[4]=2;
a[5]=5;
for(i=6;i<=n;i++)
for(j=2;j<i;j++){
a[i]+=a[j]*a[i-j+1];
}
cout<<a[n]<<endl;
return 0;
}
错排
没写代码(QAQ)
公式:f(x)=(n-1)*(f(x-1)+f(x-2))
组合数公式
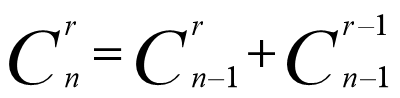
卡特兰数&错排&一个一直记不住的公式的更多相关文章
- 卡特兰数-Catalan数
卡特兰数的含义: 说到卡特兰数,就不得不提及卡特兰数序列.卡特兰数序列是一个整数序列.其通项公式是我们从中取出的就叫做第n个卡特兰数数,前几个卡特兰数数是:1, 1, 2, 5, 14, 42, 13 ...
- 错排问题 && 洛谷 P1595 信封问题
传送门 一道裸的错排问题 错排问题 百度百科上这样说 就是对于一个排列,每一个数都不在正确的位置上的方案数.n 个元素的错排数记为 D(n). 公式 D(n)=(n−1)∗(D(n−2)+D(n−1) ...
- [HDU 2049] 不容易系列之(4)——考新郎 (错排问题)
不容易系列之(4)——考新郎 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2049 题目大意: 有N对新婚夫妇,其中所有的新娘站成一列,都盖上了红布. ...
- hdu 1130 How Many Trees? 【卡特兰数】
题目 题意:给你一个数字n,问你将1~n这n个数字,可以组成多少棵不同的二叉搜索树. 1,2,5,14--根据输出中的规律可以看出这是一个卡特兰数的序列.于是代用卡特兰数中的一个递推式: 因为输入可取 ...
- BZOJ 4517: [Sdoi2016]排列计数 错排公式
4517: [Sdoi2016]排列计数 题目连接: http://www.lydsy.com/JudgeOnline/problem.php?id=4517 Description 求有多少种长度为 ...
- hdu2049 不容易系列之(4)——考新郎 错排+组合 一共有N对新婚夫妇,N个新娘随机坐成一排,每个新郎只能选一个, 其中有M个新郎找错了新娘,求发生这种情况一共有多少种可能.
不容易系列之(4)——考新郎 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)To ...
- E - 不容易系列之(4)――考新郎 错排数公式
国庆期间,省城HZ刚刚举行了一场盛大的集体婚礼,为了使婚礼进行的丰富一些,司仪临时想出了有一个有意思的节目,叫做"考新郎",具体的操作是这样的: 首先,给每位新娘打扮得几乎一模一 ...
- 容斥原理--计算错排的方案数 UVA 10497
错排问题是一种特殊的排列问题. 模型:把n个元素依次标上1,2,3.......n,求每一个元素都不在自己位置的排列数. 运用容斥原理,我们有两种解决方法: 1. 总的排列方法有A(n,n),即n!, ...
- hdu1465不easy系列之中的一个(错排)
版权声明:本文为博主原创文章,未经博主同意不得转载. vasttian https://blog.csdn.net/u012860063/article/details/37512659 转载请注明出 ...
随机推荐
- js常用方法(。。。。不完整)
lastIndexOf();substring();split();slice();splice(); var s="http://www.baidu.com"; var unit ...
- [原创]java WEB学习笔记41:简单标签之带属性的自定义标签(输出指定文件,计算并输出两个数的最大值 demo)
本博客为原创:综合 尚硅谷(http://www.atguigu.com)的系统教程(深表感谢)和 网络上的现有资源(博客,文档,图书等),资源的出处我会标明 本博客的目的:①总结自己的学习过程,相当 ...
- debian下使用ft232为stm32f429i-discovery烧写uboot和uImage
操作系统:debian 软件: openocd minicom 硬件: MiniUSB线.stm32f429i-discovery, WaveShare FT232串口模块(可以在淘宝上买到) 关 ...
- android电池(五):电池 充电IC(PM2301)驱动分析篇【转】
本文转载自:http://blog.csdn.net/xubin341719/article/details/8970363 android充电这块,有的电源管理芯片内部包含充电管理,如s5pv210 ...
- poj 1258 最小生成树 模板
POJ 最小生成树模板 Kruskal算法 #include<iostream> #include<algorithm> #include<stdio.h> #in ...
- Mysql远程链接访问权限设置
Host 'XXX' is not allowed to connect to this MySQL server 解决方案/如何开启MySQL的远程帐号 如何开启MySQL的远程帐号-1)首先以 r ...
- Delphi - 数组和结构体
技术交流,DH讲解. 记得很早之前我就说过,数组和结构体在内存中其实一样的,他们都是连续分布的.例如: ? 1 2 3 4 TMyStruct = record A,B,C:Integer; en ...
- 机器学习(十七)— SVD奇异值分解
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域.是 ...
- Linux下重命名文件或文件夹(mv命令与rename命令)
在Linux下重命名文件或目录,可以使用mv命令或rename命令 mv ———————————— mv命令既可以重命名,又可以移动文件或文件夹. 例子:将目录A重命名为B mv A B 例子:将/a ...
- 【leetcode刷题笔记】N-Queens
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens ...
