BP神经网络分类器的设计

1.BP神经网络训练过程论述
　　BP网络结构有3层：输入层、隐含层、输出层，如图1所示。

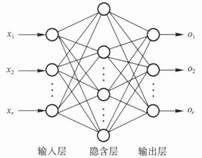
图1 三层BP网络结构
　　3层BP神经网络学习训练过程主要由4部分组成：输入模式顺传播（输入模式由输入层经隐含层向输出层传播计算）、输出误差逆传播（输出的误差由输出层经隐含层传向输入层）、循环记忆训练（模式顺序传播与误差逆传播的计算过程反复交替循环进行）和学习结果判别（判定全局误差是否趋向极小值）。

　　下面具体介绍和分析用梯度下降法训练BP神经网络，在第1次输入样品（1=1，2，……，N）进行训练时各个
　　参数的表达及计算方法。
　　（1）确定参数。

输入向量为X=[x1，x2，…，xn]T（n—输入层单元个数）；
输出向量Y=[y1，y2，…，yq]T（q—输出层单元个数）；
希望输出向量O=[o1，o2，…，oq]T；
隐含层输出向量B=[b1，b2，…，bp]T（p—隐含层单元个数）；
初始化输入层至隐含层的连接权值Wj=[wj1，wj2，…，wjt，…，wjn]T，j=1，2，…，p；
初始化隐含层至输出层的连接权值Wk=[wk1，wk2，…，wkj，…，wkp]T，k=1，2，…，q。

（2）输入模式顺序传播。

这一过程主要是利用输入模式求出它对应的实际输出。

计算隐含层各神经元的激活值：
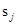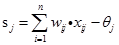　　（j=1,2,3…p）

为隐含层单元的阈值

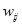为输出层至隐含层的连接权

激活函数用S型函数，即：

这里之所以选S型函数为BP神经网络神经元的激活函数，是因为它是连续可微分的，而且更接近于生物神经元的信号输出形式。

计算隐含层j单元的输出值：

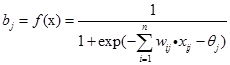
阈值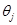在学习过程中和权值一样不断被修改，阈值的作用反应在函数的输出曲线上，

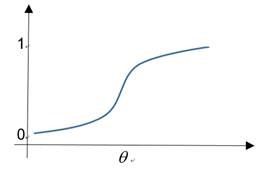
图3 阈值的作用

由图可见阈值的作用相当于输出值移了个单位。同理可求出输出端的激活值和输出值。

计算输出层第k个单元的激活值：

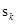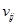为隐含层至输出层的权值

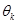输出层单元阈值

计算输出层第k个单元的实际输出值：

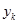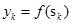（t=1,2,3…q）

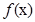为S型激活函数。

（3）输出误差的传播。

在第（2）步的模式顺传播计算中得到网络的实际输出值，当这些实际的输出值与希望的输出值不一样时或者说误差大于所限定的数值时，就要对网络进行校正。
①输出层的校正误差为：

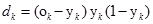（k=1，2，3…q）

②隐含层各单元的校正误差为：

③对于输出层至隐含层连接权和输出层阈值的校正量为：

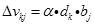
α为学习系数，α>0。

为隐含层j单元的输出。

为输出层的校正误差。
　　

④隐含层至输入层的校正量为：

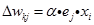
　　为隐含层j单元的校正误差。

　　（4）循环记忆训练。对于BP神经网络输入的每一组训练模式，一般都要经过数百次甚至上万次的循环记忆训练，才能使网络记住这一模式。这种循环记忆训练实际上就是反复重复上面介绍的输入模式。
　　（5）学习结果的判别。判别的目的主要是检查输出误差是否已经小到可以允许的程度。学习或者说训练的过程是网络全局误差趋向于极小值的过程。
2.BP神经网络分类器设计
　任务一：2bit异或问题，输入及其对应的输出

input=[0 0 ;

0 1;

1 0;

1 1];

output=[0;1;1;0];

2个输入神经元，2个隐含层神经元，1个输出层神经元，MATLAB代码如下：

% % % % % % % % % % % % % % %

% name:bpnet1.m

% function:solve 2bit XOR Problem with a Neural bpnetwork

% input:no

% return:no

% programer:LI Xin

% % % % % % % % % % % % % % %

clear;clc;close all;

sigma=0.01;%精度控制参数

alpha=0.8;%学习率

M=10000;%循环的最大次数

in_num=2; %输入节点个数

mid_num=2;%隐含层神经元个数

out_num=1;%输出层神经元个数

input=[0 0 ;

0 1;

1 0;

1 1];

output=[0;1;1;0];

hide_s=zeros(1,mid_num);%隐含层的激活值

hide_o=zeros(1,mid_num);%隐含层的输出值

delta_h=zeros(1,mid_num);%隐含层各联结权的修改量组成的向量

sita_h = rand(1,mid_num) ;%隐含层的阈值

sita_o=rand(1,out_num) ;%输出层阈值

output_o=zeros(1,out_num);%输出层的输出值

output_s=zeros(1,out_num);%输出层的激活值

delta_o=zeros(1,out_num); %输出层各联结权的修改量组成的向量

T=4;%样本个数

w=rand(in_num,mid_num,'double');%初始化输入层到隐含层连接权值

v=rand(mid_num,out_num,'double'); %初始化隐含层到输出层连接权值

E = sigma + 1;

N = 0;

while((E>sigma)&&(N<M))

N=N+1;

for t=1:T

for i=1:mid_num

hide_s(i)=0;

for j=1:in_num

hide_s(i)=hide_s(i)+w(j,i)*input(t,j);

end

hide_s(i)=hide_s(i)-sita_h(i); % 计算隐含层各神经元的激活值hide_s

hide_o(i)=1.0/(1.0+exp(-hide_s(i))); %隐含层神经元的输出值

end

for i=1:out_num

output_s(i)=0;

for j=1:mid_num

output_s(i)=output_s(i)+v(j,i)*hide_o(j);

end

output_s(i)=output_s(i)-sita_o(i); %计算输出层各神经元的激活值output_s

output_o(i)=1.0/(1.0+exp(-output_s(i))); % 输出层神经元的输出值

end

for i=1:out_num

delta_o(i)=output_o(i) * ( 1 - output_o(i) ) * ( output(t,i) - output_o(i) );

%输出层的校正误差delta_o=(o-y)y(1-y)

sita_o(i)=sita_o(i)-alpha*delta_o(i); %输出层阈值校正量

end

for i=1: mid_num

Z = 0;

for j=1:out_num

Z = Z+v(i,j) * delta_o(j);

end

delta_h(i) = Z * hide_o(i) * ( 1 - hide_o(i) ); %隐含层的校正误差

sita_h(i) = sita_h(i)-alpha * delta_h(i); %隐含层阈值校正量

end

for i=1: mid_num

for j=1:out_num

v(i,j) = v(i,j) +alpha * hide_o(i) * delta_o(j); %输出层至隐含层权值校正

end

for i=1:in_num

for j=1: mid_num

w(i,j) = w(i,j)+alpha * input(t,i) * delta_h(j); %隐含层至输入层权值的校正

end

E=0;

for t=1:T

for i=1:mid_num

hide_s(i) = 0;

for j=1:in_num

hide_s(i) = hide_s(i)+w(j,i) * input(t,j);

end

hide_s(i) = hide_s(i)-sita_h(i); %计算隐含层各神经元的激活值hide_s

hide_o(i) = 1.0 / ( 1.0 + exp(-hide_s(i)) ); %隐含层神经元的输出值

end

for i=1: out_num

output_s(i) = 0;

for j=1:mid_num

output_s(i) = output_s(i)+v(j,i) * hide_o(j);

end

output_s(i) = output_s(i)-sita_o(i); %计算输出层各神经元的激活值output_s

output_o(i) = 1.0 / ( 1.0 + exp(-output_s(i)) ); %输出层神经元的输出值

end

error = 0;

for i=1:out_num

error = error +( output_o(i) - output(t,i)) * ( output_o(i) - output(t,i) );

end

E = E +error / 2;

end

str=sprintf('网络学习%d次结束，误差为：%d，各层权值如下：',N,E);

disp(str)

disp('输入层到隐藏层权值：');

for i=1:in_num

for j=1:mid_num

str=sprintf('w[%d,%d]=%d',i,j,w(i,j)) ;

disp(str)

end

disp('隐藏层到输出层权值：');

for i=1:mid_num

for j=1:out_num

str=sprintf('v[%d,%d]=%d',i,j,v(i,j));

disp(str)

end

disp('对应着样本实际输出为:')

for t=1: T

str=sprintf('第%d个样本',t);

disp(str)

for i=1:mid_num

hide_s(i) = 0;

for j=1:in_num

hide_s(i) = hide_s(i)+w(j,i) * input(t,j);

end

hide_s(i) = hide_s(i)-sita_h(i); %计算隐含层各神经元的激活值hide_s

hide_o(i) = 1.0 / ( 1.0 + exp(-hide_s(i)) ); %隐含层神经元的输出值

end

for i=1: out_num

output_s(i) = 0;

for j=1:mid_num

output_s(i) = output_s(i)+v(j,i) * hide_o(j);

end

output_s(i) = output_s(i)-sita_o(i); %计算输出层各神经元的激活值output_s

output_o(i) = 1.0 / ( 1.0 + exp(-output_s(i)) ); %输出层神经元的输出值

end

disp('输入样本')

disp(input(t,:))

disp('输出样本')

disp(output_o)

end

任务二：识别问题，输入输出如下：

input=[0 0 0 0 0 0 0 1;

0 0 0 0 0 0 1 0 ;

0 0 0 0 0 1 0 0 ;

0 0 0 0 1 0 0 0 ;

0 0 0 1 0 0 0 0 ;

0 0 1 0 0 0 0 0 ;

0 1 0 0 0 0 0 0 ;

1 0 0 0 0 0 0 0 ];

output=[0 0 0 0 0 0 0 1;

0 0 0 0 0 0 1 0 ;

0 0 0 0 0 1 0 0 ;

0 0 0 0 1 0 0 0 ;

0 0 0 1 0 0 0 0 ;

0 0 1 0 0 0 0 0 ;

0 1 0 0 0 0 0 0 ;

1 0 0 0 0 0 0 0 ];

8个输入神经元，3个隐含层神经元，8个输出层神经元，详细代码与任务一差别不大，在此不再赘述，详见附件bpnet2.m

3.实验过程

对于任务一的异或问题，令学习率为0.8，迭代次数上限10000次，精度0.01，写好代码后运行结果如下：

网络学习2054次结束，误差为：9.987865e-03，各层权值如下：

输入层到隐藏层权值：

w[1,1]=-4.319853e+00

w[1,2]=-6.118312e+00

w[2,1]=4.479814e+00

w[2,2]=5.661403e+00

隐藏层到输出层权值：

v[1,1]=-6.512379e+00

v[2,1]=6.853598e+00

对应着样本实际输出为:

第1个样本

输入样本

0 0

输出样本

0.0724

第2个样本

输入样本

0 1

输出样本

0.9411

第3个样本

输入样本

1 0

输出样本

0.9128

第4个样本

输入样本

1 1

输出样本

0.0605

可见其学习后的输出和期望输出差距不大。

对于任务二的识别问题，令学习率为0.8，迭代次数上限10000次，精度0.01，写好代码后运行结果如下：

网络学习5786次结束，误差为：9.998725e-03，各层权值如下：

输入层到隐含层权值：

w[1,1]=-3.179389e+00

w[1,2]=4.680957e+00

w[1,3]=-2.814682e+00

w[2,1]=5.307254e+00

w[2,2]=3.485574e+00

w[2,3]=5.443434e+00

w[3,1]=-5.120963e+00

w[3,2]=-3.003381e+00

w[3,3]=-2.533489e-01

w[4,1]=1.072151e-01

w[4,2]=-4.017080e+00

w[4,3]=5.120281e+00

w[5,1]=5.281661e+00

w[5,2]=-4.188798e+00

w[5,3]=1.327247e-01

w[6,1]=-4.166501e+00

w[6,2]=3.666821e+00

w[6,3]=4.480010e+00

w[7,1]=4.666180e+00

w[7,2]=4.637388e+00

w[7,3]=-2.178645e+00

w[8,1]=3.595688e-01

w[8,2]=-1.660022e+00

w[8,3]=-5.989204e+00

隐藏层到输出层权值：

v[1,1]=-7.888675e+00

v[1,2]=7.121264e+00

v[1,3]=-1.422755e+01

v[1,4]=-1.645257e+00

v[1,5]=1.155231e+01

v[1,6]=-8.289016e+00

v[1,7]=8.183556e+00

v[1,8]=1.246045e+00

v[2,1]=6.724860e+00

v[2,2]=3.464005e+00

v[2,3]=-8.313719e+00

v[2,4]=-8.505718e+00

v[2,5]=-8.905993e+00

v[2,6]=4.500327e+00

v[2,7]=5.055143e+00

v[2,8]=-7.146627e+00

v[3,1]=-8.436705e+00

v[3,2]=7.793561e+00

v[3,3]=-2.065419e+00

v[3,4]=1.213004e+01

v[3,5]=-6.566507e-01

v[3,6]=7.878356e+00

v[3,7]=-8.415250e+00

v[3,8]=-1.719139e+01

对应着样本实际输出为:

第1个样本

输入样本

0 0 0 0 0 0 0 1

输出样本

Columns 1 through 7

0.0056 0.0000 0.0275 0.0001 0.0319 0.0000 0.0151

Column 8

0.9546

第2个样本

输入样本

0 0 0 0 0 0 1 0

输出样本

Columns 1 through 7

0.0154 0.0232 0.0000 0.0000 0.0055 0.0000 0.9731

Column 8

0.0207

第3个样本

输入样本

0 0 0 0 0 1 0 0

输出样本

Columns 1 through 7

0.0150 0.0234 0.0028 0.0144 0.0000 0.9735 0.0000

Column 8

0.0000

第4个样本

输入样本

0 0 0 0 1 0 0 0

输出样本

Columns 1 through 7

0.0000 0.0188 0.0000 0.0225 0.9645 0.0000 0.0094

Column 8

0.0229

第5个样本

输入样本

0 0 0 1 0 0 0 0

输出样本

Columns 1 through 7

0.0000 0.0163 0.0236 0.9647 0.0238 0.0178 0.0000

Column 8

0.0000

第6个样本

输入样本

0 0 1 0 0 0 0 0

输出样本

Columns 1 through 7

0.0046 0.0000 0.9598 0.0287 0.0003 0.0054 0.0000

Column 8

0.0280

第7个样本

输入样本

0 1 0 0 0 0 0 0

输出样本

Columns 1 through 7

0.0000 0.9647 0.0000 0.0034 0.0040 0.0110 0.0159

Column 8

0.0000

第8个样本

输入样本

1 0 0 0 0 0 0 0

输出样本

Columns 1 through 7

0.9768 0.0000 0.0130 0.0000 0.0000 0.0210 0.0191

Column 8

0.0122

4.实验总结

可见本次实验较好的完成了bp神经网络的建模，在学习率和误差精度上都达到了要求，通过这次实验深入的理解了神经网络的结构和各参数之间的作用，为以后的科研学习打下了一定基础，对于第二个任务要比第一个任务计算耗时大很多，可见bp神经网络是收敛速度比较慢。