AABB碰撞盒

矩形边界框（转）

另一种常见的用来界定物体的几何图元是矩形边界框，矩形边界框可以是与轴对齐的或是任意方向的。轴对齐矩形边界框有一个限制，就是它的边必须垂直于坐标轴。缩写AABB常用来表示axially aligned bounding box(轴对齐矩形边界框)，OBBoriented bounding box(方向矩形边界框)。轴对齐矩形边界框不仅容易创建，而且易于使用。

一个3D的AABB就是一个简单的六面体，每一边都平行于一个坐标平面。矩形边界框不一定是立方体，它的长、宽、高可以彼此不同。在图12.10中，画出了一些简单的3D物体和它们的AABB

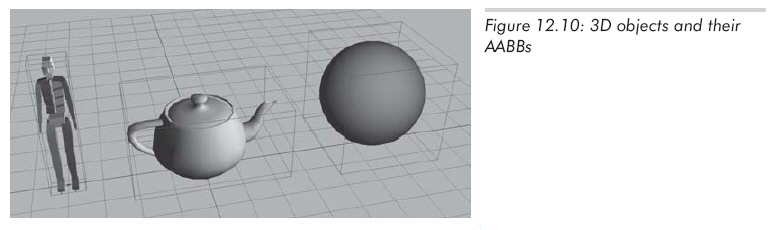
AABB的表达方法

先介绍AABB的一些重要性质和引用这些值时所用到的记法。AABB内的点满足下列等式：

xmin x xmax

ymin y ymax

zmin z zmax

特别重要的两个点为：

pmin = [xmin   ymin   zmin ]

pmax = [xmax   ymax   zmax ]

中心点c为：

c = (pmin + pmax) /2

""spminpmax的向量，包含了矩形边界的长、宽、高：

s = pmax - pmin

还可以求出矩形边界框的""r，它是从中心指向pmax的向量：

r = pmax - c = s/2

明确地定义一个AABB只需要pmin、pmaxcsr这5个向量中的两个（除sr不能配对外，它们中的任意两个都可配对）。在一些情况下，某些配对形式比其他的会更有用。我们建议用pmin和pmax表示一个边界框，因为实际应用中，使用它们的频率远高于csr。当然，由pmin和pmax计算其余三个中的任意一个都是很容易的。

在我们的C++代码中，使用下面的类表示AABB，这是一个缩略的代码清单。

    #ifndef AABB3_H
    #define AABB3_H

#include "vector3.h"

class cMatrix4x3;

//---------------------------------------------------------------------------
    // Implement a 3D axially aligned bounding box
    //---------------------------------------------------------------------------
    class cAABB3
    {
    public:
        cVector3 min, max;

public// query for dimentions
        cVector3 size() constreturn max - min; }
        float     x_size()            { return max.x - min.x; }
        float     y_size()            { return max.y - min.y; }
        float     z_size()            { return max.z - min.z; }
        cVector3 center() constreturn (min + max) * 0.5f; }

// fetch one of the eight corner points
        cVector3 corner(const// "Empty" the box, by setting the values to really large/small numbers.
     empty();

// add a point to the box
    const cVector3& p);

// add an AABB to the box
    const cAABB3& box);

// return true if the box is empty
     is_empty() const// return true if the box contains a point
     contains(const cVector3& p) const// transform the box and compute the new AABB
     set_to_transformed_box(const cAABB3& box, const cMatrix4x3& m);

// return the clostet point on this box to another point
        cVector3 clostet_point_to(const cVector3& p) const#endif

计算AABB

计算一个顶点集合的AABB是非常简单的，先将最小值和最大值设为"正负无穷大"或任何比实际中用到的数都大或小得多的数。接着，遍历全部点，并扩展边界框直到它包含所有点为止。

我们在cAABB类中引入了两个辅助函数，第一个函数负责""AABB

    //---------------------------------------------------------------------------
    // "Empty" the box, by setting the values to really large/small numbers.
    //---------------------------------------------------------------------------
     cAABB3::empty() 
    {
        constfloat big_number = 1e37f;

min.x = min.y = min.z = big_number;
        max.x = max.y = max.z = -big_number;
    }

第二个函数将单个点""到AABB中，并在必要的时候扩展AABB以包含每个点：

    //---------------------------------------------------------------------------
    // Add a point to the box
    //---------------------------------------------------------------------------
     cAABB3::add(const cVector3& p)
    {
        // expand the box as necessary to contain the point
    (p.x < min.x)        min.x = p.x;
        (p.x > max.x)        max.x = p.x;
        (p.y < min.y)        min.y = p.y;
        (p.y > max.y)        max.y = p.y;
        (p.z < min.z)        min.z = p.z;
        (p.z > max.z)        max.z = p.z;
    }

现在，从一个点集创建矩形边界框，可以使用下面的代码：

    Listing 12.1: Computing the AABB  of points

// Our list of points
    const n;
    Vector3 list[n];

// First, empty the box
    AABB3 box;
    box.empty();

// Add each point into the box
     i = 0 ; i < n ; ++i) 
      box.add(list[i]);

取得AABB的顶点：

    //--------------------------------------------------------------------------------------
    // Return one of the 8 corner points.  The points are numbered as follows:
    //
    //            6                                7
    //              ------------------------------
    //             /|                           /|
    //            / |                          / |
    //           /  |                         /  |
    //          /   |                        /   |
    //         /    |                       /    |
    //        /     |                      /     |
    //       /      |                     /      |
    //      /       |                    /       |
    //     /        |                   /        |
    //  2 /         |                3 /         |
    //   /----------------------------/          |
    //   |          |                 |          |
    //   |          |                 |          |      +Y
    //   |        4 |                 |          | 
    //   |          |-----------------|----------|      |
    //   |         /                  |         /  5    |
    //   |        /                   |        /        |       +Z
    //   |       /                    |       /         |
    //   |      /                     |      /          |     /
    //   |     /                      |     /           |    /
    //   |    /                       |    /            |   /
    //   |   /                        |   /             |  /
    //   |  /                         |  /              | /
    //   | /                          | /               |/
    //   |/                           |/                ----------------- +X
    //   ------------------------------
    //  0                              1
    //
    // Bit 0 selects min.x vs. max.x
    // Bit 1 selects min.y vs. max.y
    // Bit 2 selects min.z vs. max.z
    //--------------------------------------------------------------------------------------
    cVector3 cAABB3::corner(const
    {
        assert(i >= 0 && i <= 7);    // make sure index is in range
    return cVector3((i & 1) ? max.x : min.x,
                        (i & 2) ? max.y : min.y,
                        (i & 4) ? max.z : min.z);
    }

其他的相关函数，具体功能详见注释：

    //---------------------------------------------------------------------------
    // Add an AABB to the box
    //---------------------------------------------------------------------------
     cAABB3::add(const cAABB3& box)
    {
        // expand the box as necessary
    (box.min.x < min.x)    min.x = box.min.x;
        (box.min.x > max.x)    max.x = box.min.x;
        (box.min.y < min.y)    min.y = box.min.y;
        (box.min.y > max.y)    max.y = box.min.y;
        (box.min.z < min.z)    min.z = box.min.z;
        (box.min.z > max.z)    max.z = box.min.z;
    }

//---------------------------------------------------------------------------
    // Return true if the box is empty
    //---------------------------------------------------------------------------
     cAABB3::is_empty() const// check if we're inverted on any axis
    return (min.x > max.x) || (min.y > max.y) || (min.z > max.z);
    }

//---------------------------------------------------------------------------
    // Return true if the box contains a point
    //---------------------------------------------------------------------------
     cAABB3::contains(const cVector3& p) const// check for overlap on each axis
    return (p.x >= min.x) && (p.x <= max.x) &&
               (p.y >= min.y) && (p.y <= max.y) &&
               (p.z >= min.z) && (p.z <= max.z);
    }

//---------------------------------------------------------------------------
    // return the closest point on this box to another point
    //---------------------------------------------------------------------------
    cVector3 cAABB3::clostet_point_to(const cVector3& p) const// "push" p into the box, on each dimension.

cVector3 r;

(p.x < min.x)
            r.x = min.x;
        (p.x > max.x)
            r.x = max.x;

r.x = p.x;

(p.y < min.y) 
            r.y = min.y;
        (p.y > max.y) 
            r.y = max.y;

r.y = p.y;

(p.z < min.z)
            r.z = min.z;
        (p.z > max.z)
            r.z = max.z;

r.z = p.z;

return

AABB

很多情况下，AABB比边界球更适合于做定界球：

（1）计算一个点集的AABB，在编程上更容易实现，并能在较短的时间内完成。计算边界球则困难得多。

（2）对实际世界里的许多物体，AABB提供了一种""的边界。当然，对于某些物体，边界球更好（设想一个本身就是球形的物体）。在极端情况下，AABB的体积可能仅相当于边界球体积的1/2，大部分时候边界球的体积会比矩形框的体积大得多，比较一下电线杆的边界球和AABB就知道了。图12.11所示为不同物体的AABB与边界球的比较。

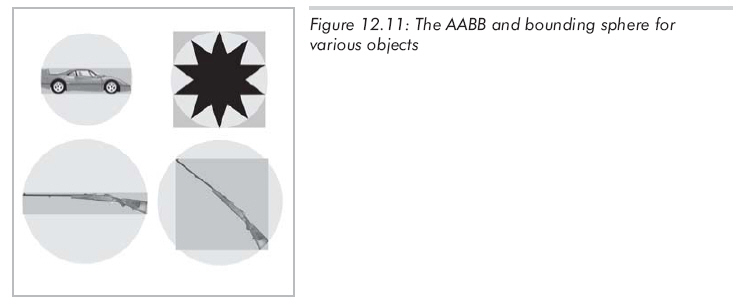
边界球的根本问题是它的形状只有一个自由度----半径，而AABB却有三个自由度----长、宽、高。因此，它可以调节这些自由度以适应不同物体。对图12.11中的大部分物体，除了右上角的星形体外，AABB都比边界球小。对这颗星，边界球也仅比AABB略小一些。通过图12.11，我们可以注意到AABB对物体的方向很敏感。比较下面两支枪的AABB，图中枪的大小都是相同的，只是方向不同而已；还应注意到在这一情况下边界球大小相同，因为边界球对物体方向不敏感。

变换AABB

当物体在虚拟世界中移动时，它的AABB也需要随之移动。此时我们有两个选择----用变换后的物体来重新计算AABB，或者对AABB做和物体同样的变换。所得到的结果不一定是轴对齐的（如果物体旋转），也不一定是盒状的（如果物体发生了扭曲）。不过，通过"变换后的AABB"进行计算要比通过"经过变换后的物体"计算AABB快得多，因为AABB只有8个顶点。

通过"变换后的AABB"计算不能只是简单地变换8个顶点，也不能通过转换原pminpmax来得到新的pminpmax ----这样可能会导致xin > xmax。为了计算新的AABB，必须先变换8个顶点，再从这8个顶点中计算一个新的AABB。

根据变换的不同，这种方法可能使新边界框比原边界框大许多。例如，在2D中，45度的旋转会大大增加边界框的尺寸，如图12.12

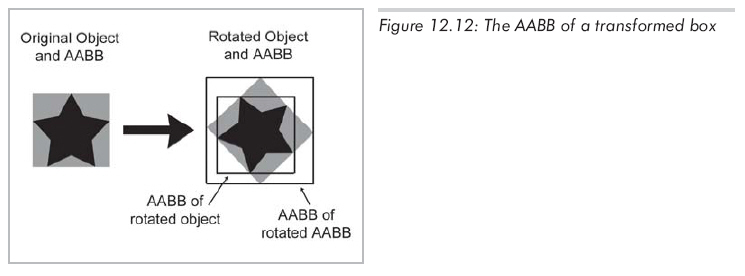
比较图12.12中原AABB（灰色框）和新AABB（右边较大的方框），它是通过旋转后的AABB计算的，新AABB几乎是原来的两倍。注意，如果从旋转后的物体而不是通过旋转后的AABB来计算新AABB，它的大小将和原来的AABB相同。

可以利用AABB的结构来加快新的AABB的计算速度，而不必先变换8个顶点，再从这8个顶点中计算新AABB。

让我们简单回顾一下3x3矩阵变换一个3D点的过程：

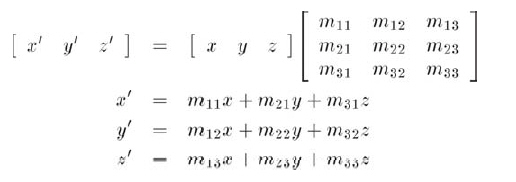
设原边界框为xminmaxymin...，新边界框计算将得到x'minx'maxy'min...。现在我们的任务就是想办法加快计算x'min的速度，换句话说，我们希望找到m11x+m21y+m31z的最小值，其中[x, y, z]是原8个顶点中的任意一个，我们所要做的就是找出这些点经过变换后谁的x坐标最小。看第一个乘积：m11x，为了最小化乘积，必须决定是用xminmax来代换其中的x。显然，如果m11>0xmin能得到最小化乘积；如果m11<0xmax能得到最小化乘积。比较方便的是，不管xminxmax中哪个被用来计算xmin，都可以用另外一个来计算xmax。可以对矩阵9个元素中的每个都应用这个计算过程，如下列代码所示：

    //---------------------------------------------------------------------------
    // Transform the box and compute the new AABB.  Remember, this always
    // results in an AABB that is at least as big as the origin, and may be
    // considerably bigger.
    //---------------------------------------------------------------------------
     cAABB3::set_to_transformed_box(const cAABB3& box, const cMatrix4x3& m)
    {
        // if we're empty, then bail.
    (box.is_empty())
        {
            empty();
            return// start with the translation portion
        min = max = get_translation(m);

// examine each of the 9 matrix elements and compute the new AABB
    (m.m11 > 0.0f)
        {
            min.x += m.m11 * box.min.x;
            max.x += m.m11 * box.max.x;
        }

{
            min.x += m.m11 * box.max.x;
            max.x += m.m11 * box.min.x;
        }

(m.m21 > 0.0f)
        {
            min.x += m.m21 * box.min.y; 
            max.x += m.m21 * box.max.y;
        }

{
            min.x += m.m21 * box.max.y; 
            max.x += m.m21 * box.min.y;
        }

(m.m31 > 0.0f)
        {
            min.x += m.m31 * box.min.z; 
            max.x += m.m31 * box.max.z;
        }

{
            min.x += m.m31 * box.max.z; 
            max.x += m.m31 * box.min.z;
        }

(m.m12 > 0.0f) 
        {
            min.y += m.m12 * box.min.x; 
            max.y += m.m12 * box.max.x;
        }

{
            min.y += m.m12 * box.max.x; 
            max.y += m.m12 * box.min.x;
        }

(m.m22 > 0.0f)
        {
            min.y += m.m22 * box.min.y; 
            max.y += m.m22 * box.max.y;
        }

{
            min.y += m.m22 * box.max.y; 
            max.y += m.m22 * box.min.y;
        }

(m.m32 > 0.0f)
        {
            min.y += m.m32 * box.min.z; 
            max.y += m.m32 * box.max.z;
        }

{
            min.y += m.m32 * box.max.z; 
            max.y += m.m32 * box.min.z;
        }

(m.m13 > 0.0f) 
        {
            min.z += m.m13 * box.min.x; 
            max.z += m.m13 * box.max.x;
        }

{
            min.z += m.m13 * box.max.x; 
            max.z += m.m13 * box.min.x;
        }

(m.m23 > 0.0f)
        {
            min.z += m.m23 * box.min.y; 
            max.z += m.m23 * box.max.y;
        }

{
            min.z += m.m23 * box.max.y; 
            max.z += m.m23 * box.min.y;
        }

(m.m33 > 0.0f)
        {
            min.z += m.m33 * box.min.z; 
            max.z += m.m33 * box.max.z;
        }

{
            min.z += m.m33 * box.max.z; 
            max.z += m.m33 * box.min.z;
        }
    }