图->连通性->无向图的连通分量和生成树
文字描述
对无向图进行遍历时,对于连通图,仅需从图中任一顶点出发,进行深度优先搜索或广度优先搜索,便可访问到图中所有顶点。但对非连通图,则需从多个顶点出发搜索,每一次从一个新的起始点出发进行搜索过程得到的顶点访问序列恰为其各个连通分量中的顶点集。
对于非连通图,每个连通分量中的顶点集,和遍历时走过的边一起构成若干棵生成树,这些连通分量的生成树组成非连通图的生成森林.
示意图
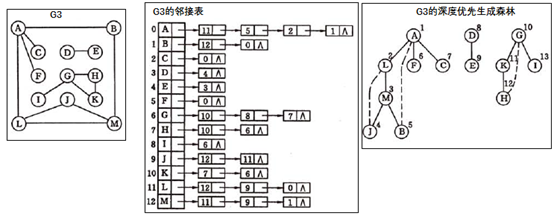

算法分析
求无向图的连通分量的生成森林的算法时间复杂度和遍历相同.
代码实现
//1.建立无向图
//2.建立无向图的深度优先生成森林, 森林转换成二叉树结构,并采用孩子兄弟链表存储
//https://www.cnblogs.com/tgycoder/p/5048898.html
//https://blog.csdn.net/qq_16234613/article/details/77431043 #include <stdio.h>
#include <stdlib.h>
#include <string.h> ///for debug start///
#include <stdarg.h>
#define DEBUG(args...) debug_(__FILE__, __FUNCTION__, __LINE__, ##args)
void debug_(const char* file, const char* function, const int line, const char *format, ...)
{
char buf[] = {};
sprintf(buf, "[%s,%s,%d]", file, function, line); va_list list;
va_start(list, format);
vsprintf(buf+strlen(buf), format, list);
va_end(list); printf("%s\n", buf); }
///for debug end/// #define INFINITY 100000
#define MAX_VERTEX_NUM 20
#define None -1
typedef enum {DG, DN, UDG, UDN} GraphKind;
typedef char VertexType;
typedef struct{char note[];}InfoType;
//弧结点
typedef struct ArcNode{
int adjvex;//该弧所指向的顶点的位置
struct ArcNode *nextarc;//指向下一条弧的结点
InfoType *info;//与该弧相关的其他信息
}ArcNode;
typedef struct VNode{
VertexType data;//顶点信息
ArcNode *firstarc;//指向第一条依附该顶点的弧的指针
}VNode, AdjList[MAX_VERTEX_NUM]; typedef struct{
AdjList vertices;//存放图的头结点的链表
int vexnum;//图的顶点数
int arcnum;//图的弧数
int kind;//图类型
}ALGraph; //返回图G中顶点信息委v的顶点位置
int LocateVex(ALGraph G, VertexType v)
{
int i = ;
for(i=; i<G.vexnum; i++){
if(G.vertices[i].data == v){
return i;
}
}
return -;
} //返回图G的顶点位置为loc的顶点信息
VertexType GetVex(ALGraph G, int loc)
{
return G.vertices[loc].data;
} //在链表L的头部插入顶点v
int InsFirst(ArcNode *L, int v)
{
ArcNode *n = (ArcNode *)malloc(sizeof(struct ArcNode));
n->adjvex = v;
n->nextarc = L->nextarc;
L->nextarc = n;
return ;
} //返回图G中与顶点v相连的第一个顶点在图中的位置
int FirstAdjVex(ALGraph G, int v)
{
return G.vertices[v].firstarc->nextarc->adjvex;
} //返回图G中与顶点v相邻的w的下一个相邻的定点在图中的位置
int NextAdjVex(ALGraph G, int v, int w)
{
ArcNode *arc = G.vertices[v].firstarc;
while(arc && arc->adjvex != w){
arc = arc->nextarc;
}
if(arc && arc->nextarc){
return arc->nextarc->adjvex;
}
return None;
} //创建一个无向图
int CreateUDG(ALGraph *G){
printf("!以邻接表作为图的存储结构创建无向图!\n");
G->kind = UDG;
int i = , j = , k = , IncInfo = ;
int v1 = , v2 = ;
char tmp[] = {};
printf("输入顶点数,弧数:");
scanf("%d,%d", &G->vexnum, &G->arcnum);
for(i=; i<G->vexnum; i++){
printf("输入第%d个顶点: ", i+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
G->vertices[i].data = tmp[];
G->vertices[i].firstarc = malloc(sizeof(struct ArcNode));
G->vertices[i].firstarc->adjvex = None;
G->vertices[i].firstarc->nextarc = NULL;
}
for(k=; k<G->arcnum; k++){
printf("输入第%d条弧(顶点1, 顶点2): ", k+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
sscanf(tmp, "%c,%c", (char *)&v1, (char *)&v2);
i = LocateVex(*G, v1);
j = LocateVex(*G, v2);
InsFirst(G->vertices[i].firstarc, j);
InsFirst(G->vertices[j].firstarc, i);
if(IncInfo){}
}
return ;
} //打印无向图G的邻接表信息
void printALG(ALGraph G)
{
int i = ;
ArcNode *p = NULL;
for(i=; i<G.vexnum; i++){
printf("%c\t", G.vertices[i].data);
p = G.vertices[i].firstarc;
while(p){
if(p->adjvex != None){
printf("%d\t", p->adjvex);
}
p = p->nextarc;
}
printf("\n");
}
return;
} typedef VertexType TElemType;
//采用孩子兄弟链表存储结构
typedef struct{
TElemType data;
struct CSNode *firstchild;
struct CSNode *nextsibling;
}CSNode, *CSTree; //先根遍历树T
void PreOrderTraverse(CSTree T){
if(T){
printf("%c\t", T->data);
PreOrderTraverse((CSTree)T->firstchild);
PreOrderTraverse((CSTree)T->nextsibling);
return ;
}else{
return ;
}
} //中根遍历树T
void InOrderTraverse(CSTree T){
if(T){
InOrderTraverse((CSTree)T->firstchild);
printf("%c\t", T->data);
InOrderTraverse((CSTree)T->nextsibling);
return ;
}else{
return ;
}
} int visited[MAX_VERTEX_NUM];
CSTree DFSTree_q = NULL;
int ISFirst = ;
//从第v个顶点出发深度优先遍历图G,建立以T为根的生成树
void DFSTree(ALGraph G, int V, CSTree *T)
{
int w = ;
CSTree p = NULL;
visited[V] = ;
for(w=FirstAdjVex(G, V); w>=; w=NextAdjVex(G, V, w)){
if(!visited[w]){
//分配孩子结点
p = (CSTree)malloc(sizeof(CSNode));
p->data = GetVex(G, w);
p->firstchild = NULL;
p->nextsibling = NULL;
if(ISFirst){
//w是v的第一个未被访问的邻接顶点
ISFirst = ;
(*T)->firstchild = (struct CSNode *)p;
}else{
//w是v的其它未被访问的邻接顶点
//是上一个邻接顶点的右兄弟结点
DFSTree_q->nextsibling = (struct CSNode *)p;
}
DFSTree_q = p;
//从第w个顶点出发深度优先遍历图G,建立子生成树DFSTree_q
DFSTree(G, w, &DFSTree_q);
}
}
} //建立无向图G的深度优先生成森林的孩子兄弟链表T
void DFSForest(ALGraph G, CSTree *T)
{
CSTree p = NULL;
CSTree q = NULL;
*T = NULL;
int v = ;
for(v=; v<G.vexnum; v++){
visited[v] = ;
}
for(v=; v<G.vexnum; v++){
if(!visited[v]){
//第v个顶点为新的生成树的根结点
p = (CSTree)malloc(sizeof(CSNode));
p->data = GetVex(G, v);
p->firstchild = NULL;
p->nextsibling = NULL;
if(!(*T)){
//是第一颗生成树的根
*T = p;
}else{
//是其他生成树的根(前一颗的根的“兄弟”)
q->nextsibling = (struct CSNode *)p;
}
//q指示当前生成树的根
q = p;
//建立以p为根的生成树
ISFirst = ;
DFSTree(G, v, &p);
}
}
} int main(int argc, char *argv[])
{
ALGraph G;
//创建一个无向图
CreateUDG(&G);
//打印无向图中的信息
printALG(G); CSTree T;
//依照无向图G,建立一颗生成森林,并将其转换成成二叉树存储,二叉树以孩子兄弟链表存储结构存储
DFSForest(G, &T);
//先根遍历该生成树
PreOrderTraverse(T);printf("\n");
//中根遍历该生成树
InOrderTraverse(T);printf("\n");
return ;
}
无向图的深度优先生成森林算法
代码运行
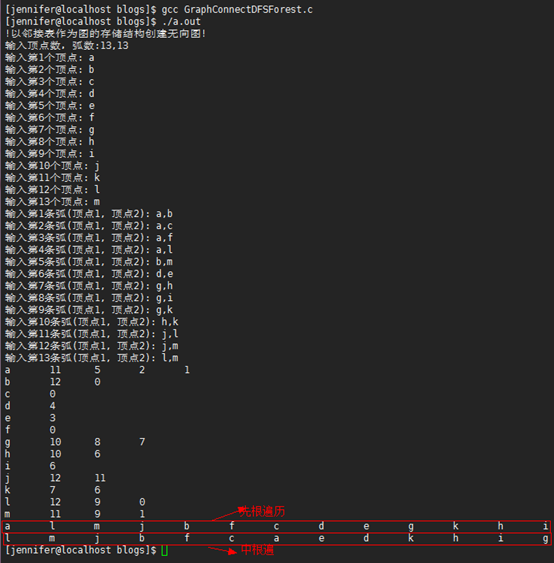
图->连通性->无向图的连通分量和生成树的更多相关文章
- 图连通性【tarjan点双连通分量、边双联通分量】【无向图】
根据 李煜东大牛:图连通性若干拓展问题探讨 ppt学习. 有割点不一定有割边,有割边不一定有割点. 理解low[u]的定义很重要. 1.无向图求割点.点双联通分量: 如果对一条边(x,y),如果low ...
- [LOJ#121]动态图连通性
[LOJ#121]动态图连通性 试题描述 这是一道模板题. 你要维护一张无向简单图.你被要求加入删除一条边及查询两个点是否连通. 0:加入一条边.保证它不存在. 1:删除一条边.保证它存在. 2:查询 ...
- BZOJ1050 [HAOI2006]旅行comf[并查集判图连通性]
★ Description 给你一个无向图,N(N<=500)个顶点, M(M<=5000)条边,每条边有一个权值Vi(Vi<30000).给你两个顶点S和T,求 一条路径,使得路径 ...
- SWUST OJ1065 无向图的连通分量计算
无向图的连通分量计算 5000(ms) 10000(kb) 2555 / 5521 假设无向图G采用邻接矩阵存储,编写一个算法求连通分量的个数. 输入 第一行为一个整数n,表示顶点的个数(顶点编号为0 ...
- LOJ121 「离线可过」动态图连通性
思路 动态图连通性的板子,可惜我不会在线算法 离线可以使用线段树分治,每个边按照存在的时间插入线段树的对应节点中,最后再dfs一下求出解即可,注意并查集按秩合并可以支持撤销操作 由于大量使用STL跑的 ...
- 【LOJ121】「离线可过」动态图连通性
[LOJ121]「离线可过」动态图连通性 题面 LOJ 题解 线段树分治的经典应用 可以发现每个边出现的时间是一个区间 而我们每个询问是一个点 所以我们将所有边的区间打到一颗线段树上面去 询问每个叶子 ...
- 【BZOJ4025】二分图(LCT动态维护图连通性)
点此看题面 大致题意: 给你一张图以及每条边的出现时间和消失时间,让你求每个时间段这张图是否是二分图. 二分图性质 二分图有一个比较简单的性质,即二分图中不存在奇环. 于是题目就变成了:让你求每个时间 ...
- POJ3177 Redundant Paths 图的边双连通分量
题目大意:问一个图至少加多少边能使该图的边双连通分量成为它本身. 图的边双连通分量为极大的不存在割边的子图.图的边双连通分量之间由割边连接.求法如下: 求出图的割边 在每个边双连通分量内Dfs,标记每 ...
- 图->连通性->关节点和重连通分量
文字描述 相关定义:假若在删去顶点v以及和v相关联的各边之后,将图的一个连通分量分割成两个或两个以上的连通分量,则称顶点v为该图的一个关节点.一个没有关节点的连通图称为重连通图. 在重连通图上,任意一 ...
随机推荐
- TCP中的KeepAlive与HTTP中的Keep-Alive
KeepAlive 与 Keep-Alive 前言 昨天被问到了HTTP中Keep-Alive的概念,看名字我只知道是保持连接用的,但是对于他怎么结束连接,为什么要用他这些就不是很清楚了,今天查了一下 ...
- golang:slice切片
一直对slice切片这个概念理解的不是太透彻,之前学习python的就没搞清楚,不过平时就用python写个工具啥的,也没把这个当回事去花时间解决. 最近使用go开发又遇到这个问题,于是打算彻底把这个 ...
- python开发-与其他语言的比较
1.关于函数 1)不需要指定返回类型,不需要指定是否有返回值,每个函数都有返回值,没有的话,就返回None 2)参数也可以不指定类型,可以有默认参数,但是必须放到最后,调用的时候指定参数的值,和顺序无 ...
- Oracle---number数据类型
NUMBER ( precision, scale) precision表示数字中的有效位;如果没有指定precision的话,Oracle将使用38作为精度. 如果scale大于零,表示数字精确 ...
- 【GMT43智能液晶模块】例程二:串口通信实验
实验原理: GMT43智能液晶模块的串口包括USB_UART(CH340),TTL,RS-232,RS-485/ RS-422等四部分,USB_UART部分通过CH340芯片与STM32F429的US ...
- 【css】zSass - 用 sass 编写 css
zSass 是自己整理的一个 sass 库,参考了 sassCore. 目录结构 variables.scss 默认值设置. reset.scss 重置浏览器样式.(参考:normalize) com ...
- Fedora Server 21 安装 搜狗拼音输入法
最新文章:Virson’s Blog 借鉴文章:博客园-怒杀神殿 ChinaUnix-firo 百度贴吧-fedora吧 方法一:解压deb安装包方式安装: 如果本机已安装ibus,需要先卸载, ...
- QTableView 二次整理
一.设置可视化的组件 参考: http://www.cnblogs.com/ribavnu/p/4810412.html 二.常用基本属性 http://www.cnblogs.com/ribavnu ...
- c# 根据字段名,得到对象中的属性值
public string GetModelValue(string FieldName, object obj) { try { Type Ts = obj.GetType(); object o ...
- Spark学习笔记——房屋价格预测
先翻译了一下给的房屋数据的特征,这里定义了一个case class,方便理解每个特征的含义, Kaggle的房价数据集使用的是Ames Housing dataset,是美国爱荷华州的艾姆斯镇2006 ...
