POJ 2369 Permutations(置换群概念题)

Description

We remind that the permutation of some final set is a one-to-one mapping of the set onto itself. Less formally, that is a way to reorder elements of the set. For example, one can define a permutation of the set {1,2,3,4,5} as follows: 
 
This record defines a permutation P as follows: P(1) = 4, P(2) = 1, P(3) = 5, etc. 
What is the value of the expression P(P(1))? It’s clear, that P(P(1)) = P(4) = 2. And P(P(3)) = P(5) = 3. One can easily see that if P(n) is a permutation then P(P(n)) is a permutation as well. In our example (believe us) 
 
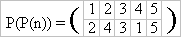
It is natural to denote this permutation by P2(n) = P(P(n)). In a general form the defenition is as follows: P(n) = P1(n), Pk(n) = P(Pk-1(n)). Among the permutations there is a very important one — that moves nothing: 
 
It is clear that for every k the following relation is satisfied: (EN)k = EN. The following less trivial statement is correct (we won't prove it here, you may prove it yourself incidentally): Let P(n) be some permutation of an N elements set. Then there exists a natural number k, that Pk = EN. The least natural k such that Pk = EN is called an order of the permutation P. 
The problem that your program should solve is formulated now in a very simple manner: "Given a permutation find its order."

Input

In the first line of the standard input an only natural number N (1 <= N <= 1000) is contained, that is a number of elements in the set that is rearranged by this permutation. In the second line there are N natural numbers of the range from 1 up to N, separated by a space, that define a permutation — the numbers P(1), P(2),…, P(N).

Output

You should write an only natural number to the standard output, that is an order of the permutation. You may consider that an answer shouldn't exceed 10⁹.

Sample Input

5
4 1 5 2 3

Sample Output

6

启发博客：http://blog.csdn.net/tc_to_top/article/details/48132609

题目大意：求将一个排列p(n)还原成En(1,2,3,4...)的最小置换次数

题目分析：计算置换中每个循环节内元素的个数，答案就是这个数的最小公倍数，很好理解，假设某个循环节包含3个元素，则这个循环节还原需要3次，另一个循环节包含2个元素，需要2次置换还原，因此我要让全部序列都还原，只需要取它们的最小公倍数即可

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<string.h>
 using namespace std;

 int a[];
 bool vis[];
 long long gcd(long long b,long long c)//计算最大公约数
 {
 return c==?b:gcd(c,b%c);
 }

 long long lcm(long long b,long long c)//计算最小公倍数
 {
 return b * c/ gcd(b, c);
 }

 int main()
 {
     int n,i,tmp,j;
     long long res;
     while(~scanf("%d",&n))
     {
         for(i=;i<=n;i++)
             scanf("%d",&a[i]);
         memset(vis,false,sizeof(vis));
         res=;
         for(i=;i<=n;i++)
         {
             if(!vis[i])
             {
                 j=i;
                 tmp=;
                 while(!vis[j])
                 {
                     vis[j]=true;
                     tmp++;
                     j=a[j];
                 }
             }
             res=lcm(res,(long long)tmp);
         }
         printf("%lld\n",res);
     }
     return ;
 }