线性代数与Python

1.向量
1.1向量例子
1.2向量加法与减法
1.3向量的乘法
2.矩阵
2.1矩阵例子
2.2矩阵的形状
2.3矩阵的创建函数

1.向量

向量是指可以加总（以生成新的向量），可以乘以标量（即数字），也可以生成新的向量的对象。

向量是有限维空间的点。

1.1向量例子

如果你有很多人的身高、体重、年龄数据，就可以把数据记为三维向量(height, weight, age)。

如果你教的一个班有四门考试，就可以把学生成绩记为四维向量(exam1, exam2, exam3, exam4)。

1.2向量加法与减法

向量以分量方式（componentwise）做运算。这意味着，如果两个向量v 和w 长度相同，那它们的和就是一个新的向量，其中向量的第一个元素等于v[0] + w[0]，第二个元素等于v[1] + w[1]，以此类推。（如果两个向量长度不同，则不能相加。）

• 向量加法函数

def vector_add(v, w):
    retrun [v_i + w_i for v_i, w_i in zip(v,w)]

• 向量减法函数

def vector_add(v, w):
    retrun [v_i - w_i for v_i, w_i in zip(v,w)]

• 多个向量的加法运算

def vector_sum(*vectors):
    result = vectors[0]
    for vector in vectors[1:]:
        result = vector_add(result, vector)
     return result

#方法2
import functools import reduce
def vector_sum(*vectors):
    return reduce(vector_add, vectors)

1.3向量的乘法

• 标量与向量的乘法

def scalar_multiply(c,v):
    return [c * v_i for v_i in v]

• 系列向量的均值

def vector_mean(*vectors):
    n = len(vectors)
    return scalar_multiply(1/n, vector_sum(vectors))

• 点乘

def dot(v,w):
    return sum(v_i * w_i for v_i, w_i in zip(v,w))

• 向量的平方和

def sum_of_squares(v)
    return dot(v,v)

• 向量的长度

import math
def magnitude(v)
    return math.sqrt(sum_of_squares(v))

• 两点间的距离
  
  

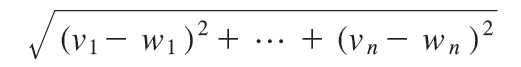
def squared_distance(v,w):
    return sum_of_squares(vector_subtract(v,w))

def distance(v,w):
    return math.squrt(squared_distance(v,w))
    # return magnitude(vector_subtract(v,w))

2.矩阵

矩阵是一个二维的数据集合。我们将矩阵表示为列表的列表，每个内部列表的大小都一样，表示矩阵的一行。如果A是一个矩阵，那么A[i][j]就表示第i行第j列的元素。按照数学表达的惯例，我们通常用大写字母表示矩阵。

2.1矩阵例子

2.2矩阵的形状

def shape(A):
    num_rows = len(A)
    num_cols = len(A[0] if A else 0)
    return num_rows, num_cols

如果一个矩阵有n 行k 列，则可以记为n×k 矩阵。我们可以把这个n×k 矩阵的每一行都当作一个长度为k 的向量，把每一列都当作一个长度为n 的向量：

2.3矩阵的创建函数

def make_matrix(num_rows, num_cols, entry_fn):
    return [[entry_fn(i, j) for j in range(num_cols)] for i in range(num_rows)]

def is_diagonal(i, j):
    return 1 if i == j else 0

make_matrix(5, 5, is_diagonal)
[[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1]]

参考《数据科学入门》