L1比L2更稀疏

1. 简单列子：

一个损失函数L与参数x的关系表示为：

则 加上L2正则化，新的损失函数L为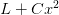：（蓝线）

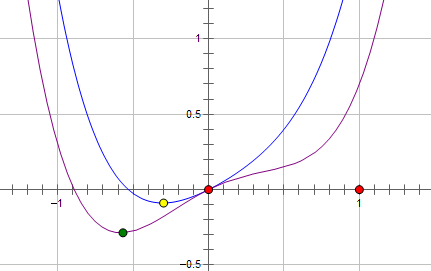
最优点在黄点处，x的绝对值减少了，但依然非零。

如果加上L1正则化，新的损失函数L为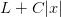：（粉线）

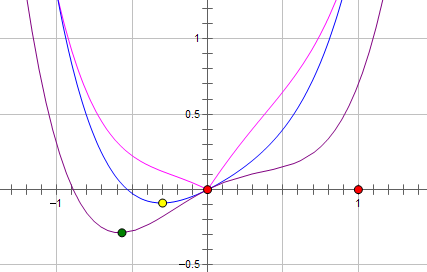
最优点为红点，变为0，L1正则化让参数的最优值变为0，更稀疏。

L1在江湖上人称Lasso，L2人称Ridge。

两种正则化，能不能将最优的参数变为0，取决于最原始的损失函数在0点处的导数，如果原始损失函数在0点处的导数不为0，则加上L2正则化之后（+2Cx），导数依然不为0。而加上L1正则化（导数为-C），如果C大于原先损失函数在0点处的导数的绝对值，x=0就变成了极小值。

2. 概念上理解：

加上正则化约束，要达到最小化损失函数，就是不能随心所欲的取参数的值了，要保证在满足的限制之内。假设有一个参数，L2的限制条件为|w|^2<c,为上图的红线，而L1的限制条件为|w|<c; L1 有角，L2无角

对于L1和L2规则化的代价函数来说，我们可以写成以下形式：

也就是说，我们将模型空间限制在w的一个L1-ball 中。为了便于可视化，我们考虑两维的情况，在(w1, w2)平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：

可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，而目标函数的测地线除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性，例如图中的相交点就有w1=0，而更高维的时候（想象一下三维的L1-ball 是什么样的？）除了角点以外，还有很多边的轮廓也是既有很大的概率成为第一次相交的地方，又会产生稀疏性。

相比之下，L2-ball 就没有这样的性质，因为没有角，所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性，而L2-regularization 不行的原因了。

因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

3. 概率上理解

如果认为数据是来自高斯密度函数，取对数后就剩一个平方项，这就是L2范式（数据来自高斯分布，应该在代价函数中加入数据先验的高斯密度函数---L2范数）

如果数据稀疏，认为来自于laplace分布，

laplace数据分布时稀疏的，laplace概率密度函数

去对数，剩下一个一次项就是L1范式。加入laplace先验作为正则项的代价函数，说明数据是稀疏的。

L2正则化相当于假设我们所求w的分布为高斯分布，L1对应的先验概率函数为拉普拉斯分布。 高斯分布对大w的概率低，对于小w的概率高，所以它限制w到一个小数，但不为0. 拉普拉斯分布对小w的概率低，希望逼近为0， 对于大w的概率比高斯分布高。

L1 更 容易稀疏化。

为什么正则化能防止过拟合：

过拟合表现在训练数据上的误差非常小，而在测试数据上误差反而增大。其原因一般是模型过于复杂，过分得去拟合数据的噪声和outliers. 正则化则是对模型参数添加先验，使得模型复杂度较小，对于噪声以及outliers的输入扰动相对较小。

我们相当于是给模型参数w 添加了一个协方差为1/alpha 的零均值高斯分布先验。 对于alpha =0，也就是不添加正则化约束，则相当于参数的高斯先验分布有着无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练数据，w可以变得任意大不稳定。alpha越大，表明先验的高斯协方差越小，模型约稳定， 相对的variance也越小。

因此为了解决过度拟合，有以下两个办法。

&amp;lt;img src="https://pic3.zhimg.com/811f033c45950d743426b9e0d2ab9bce_b.png" data-rawwidth="772" data-rawheight="322" class="origin_image zh-lightbox-thumb" width="772" data-original="https://pic3.zhimg.com/811f033c45950d743426b9e0d2ab9bce_r.png"&amp;gt;

方法一：尽量减少选取变量的数量

具体而言，我们可以人工检查每一项变量，并以此来确定哪些变量更为重要，然后，保留那些更为重要的特征变量。至于，哪些变量应该舍弃，我们以后在讨论，这会涉及到模型选择算法，这种算法是可以自动选择采用哪些特征变量，自动舍弃不需要的变量。这类做法非常有效，但是其缺点是当你舍弃一部分特征变量时，你也舍弃了问题中的一些信息。例如，也许所有的特征变量对于预测房价都是有用的，我们实际上并不想舍弃一些信息或者说舍弃这些特征变量。

方法二：正则化

正则化中我们将保留所有的特征变量，但是会减小特征变量的数量级（参数数值的大小θ(j)）。

优化目标，也就是说我们需要尽量减少代价函数的均方误差。因为，如果你在原有代价函数的基础上加上 1000 乘以 参数这一项 ，那么这个新的代价函数将变得很大，所以，当我们最小化这个新的代价函数时， 我们将使 参数 的值接近于 0，就像我们忽略了这个值一样。这种思路就是，如果我们的参数值对应一个较小值的话（参数值比较小），那么往往我们会得到一个形式更简单的假设。