P1192 台阶问题

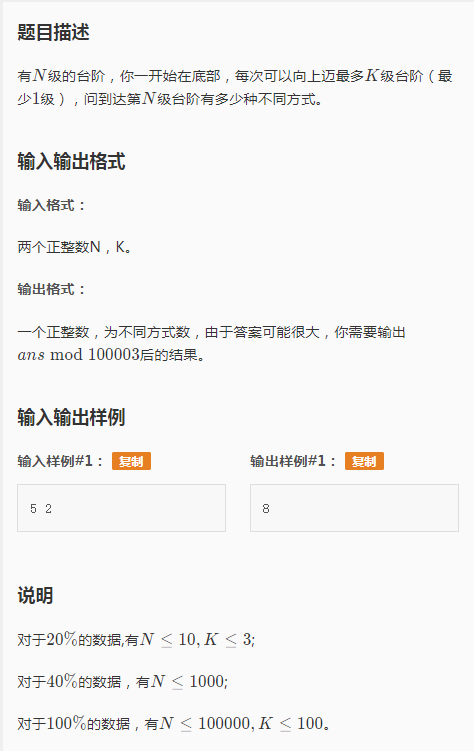
递推问题，要用到递推式：

设f(n)为n个台阶的走法总数，把n个台阶的走法分成k类：
第1类：第1步走1阶，剩下还有n-1阶要走，有f(n-1)种方法；

第2类：第1步走2阶，剩下还有n-2阶要走，有f(n-2)种方法；

第3类：第1步走3阶，剩下还有n-3阶要走，有f(n-3)种方法；

..........                    ...........

第k类：第1步走k阶，剩下还有n-k阶要走，有f(n-k)种方法；

根据加法原理：f(n)=f(n-1)+f(n-2)+.......+f(n-k)

程序如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
using namespace std;
int f[];
int main()
{
    int n,k;
    cin>>n>>k;
    f[]=;
    for(int i=;i<=n;i++)
      for(int j=;j<=k&&i-j>=;j++)     //i-j>=0必须要有
      {
          f[i]+=f[i-j];
          f[i]%=;
      }
    cout<<f[n];
    return ;
}