排序算法之NB三人组

快速排序

思路:

例如：一个列表[5,7,4,6,3,1,2,9,8],

1.首先取第一个元素5,以某种方式使元素5归位,此时列表被分为两个部分,左边的部分都比5小,右边的部分都比5大,这时列表变成了[2,1,4,3,5,6,7,9,8]
2.再对5左边进行递归排序,取5左边部分的第一个元素2,使2归位,这时5左边的部分变成了[1,2,4,3]
3.2归位后再对2右边5左边的部分即[4,3]进行排序,然后整个列表中5左边的部分就完成了排序
4.再使用递归方法对5右边的部分进行递归排序,直到把列表变成有序列表

列表就变成有序列表了.

代码实现:

def _quick_sort(data,left,right):
	if left < right:
		mid=partition(data,left,right)
		_quick_sort(data,left,mid-1)
		_quick_sort(data,mid+1,right)

def partition(li,left,right):
	print("befor sort:",li)
	tmp=li[left]

	while left <right:
		while left <right and tmp < li[right]:
			right -=1
		li[left]=li[right]

		while left <right and li[left] < tmp:
			left += 1
		li[right]=li[left]

	li[left]=tmp
	print("after sort:",li)

	return left

def quick_sort(li):
	_quick_sort(li,0,len(li)-1)

li=[5,7,4,6,3,1,2,9,8]
print(quick_sort(li))

打印结果:

befor sort: [5, 7, 4, 6, 3, 1, 2, 9, 8]
after sort: [2, 1, 4, 3, 5, 6, 7, 9, 8]
after sort: [1, 2, 4, 3, 5, 6, 7, 9, 8]
after sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
after sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
befor sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
befor sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
after sort: [1, 2, 3, 4, 5, 6, 7, 8, 9]

快排的最坏情况:

如果一个列表完全是倒序的,递归的次数为最大,等于len(li)*log(len(li))

此时可以随机取列表中的一个元素进行排序.

堆排序

树与二叉树

树是一种数据结构,比如linux的目录是呈倒树状结构
树是一种可以递归定义的数据结构
树是由n个节点组成的集合
	如果n=0,那这是一棵空树
	如果n>0,那存在1个节点作为树的根节点,其他节点可以分为m个集合,每个集合本身又是一棵树

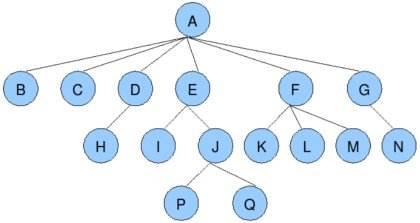
关于树的一些概念

根节点						例如 A节点
叶子节点					例如 B,C,H,I,P,Q等不再分叉的节点
树的深度(高度)				例如 上图中的树共有4层,所以这棵树的深度为4
子节点/父节点				例如 A,D,E,J等为父节点,B,C,H,I,P为子节点
子树

二叉树:度不超过2的树(节点最多有两个叉)

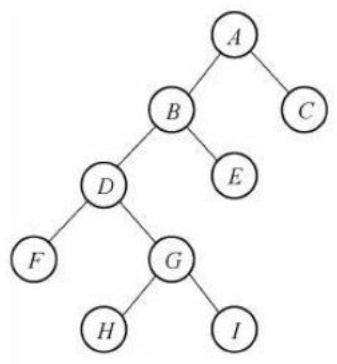
两种特殊的二叉村
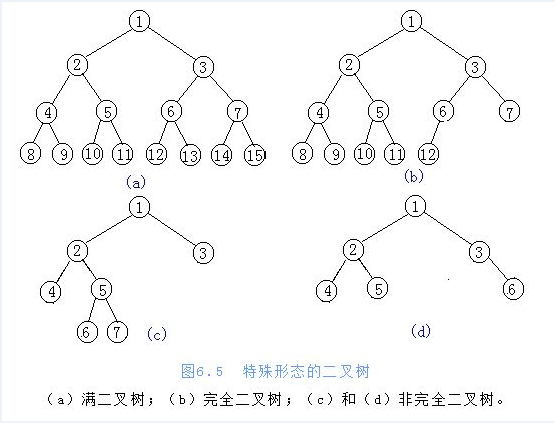
	满二叉树:除了叶子节点,所有节点都有两个子节点,且所有叶子节点的深度都相同
	完全二叉树:从满二叉树的后边拿走几个节点,就变成了完全二叉树,中间不能缺少节点

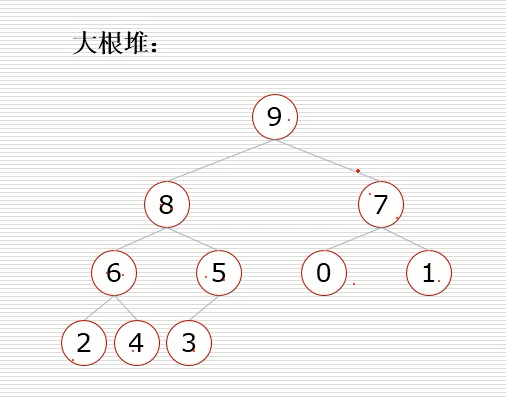
堆排序

大根堆:一棵完全二叉树,满足任一节点都比其子节点大

小根堆:一棵完全二叉树,满足任一节点都比其子节点小

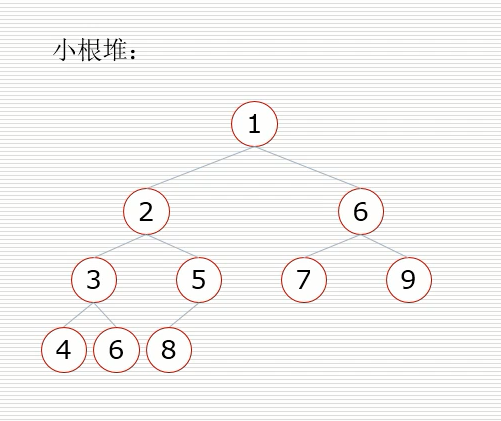
假设节点的左右子树都是堆,但自身不是堆,

当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变换成一个堆

构造堆

首先有这样一棵二叉树,

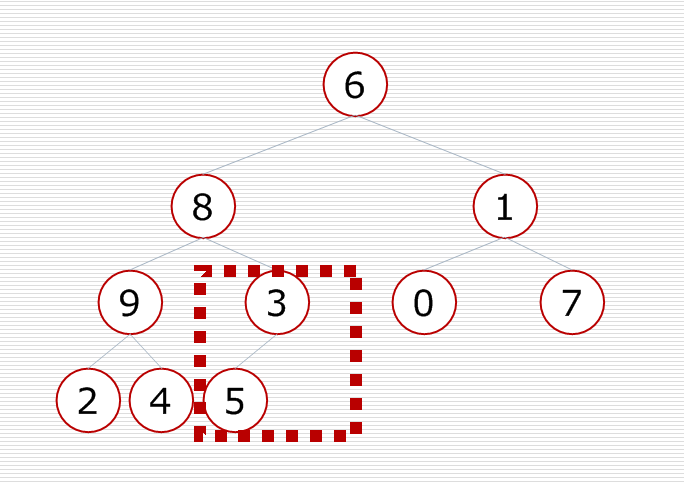
先调整最后一个小子树,把大的元素放到这个小子树的顶部,使小子树变成一个堆

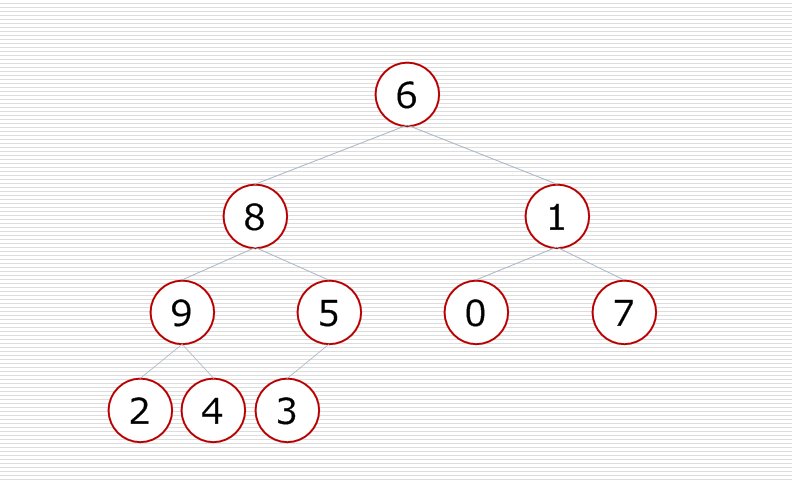
再对倒数第二个小子树进行调整,使这个小子树变成一个堆

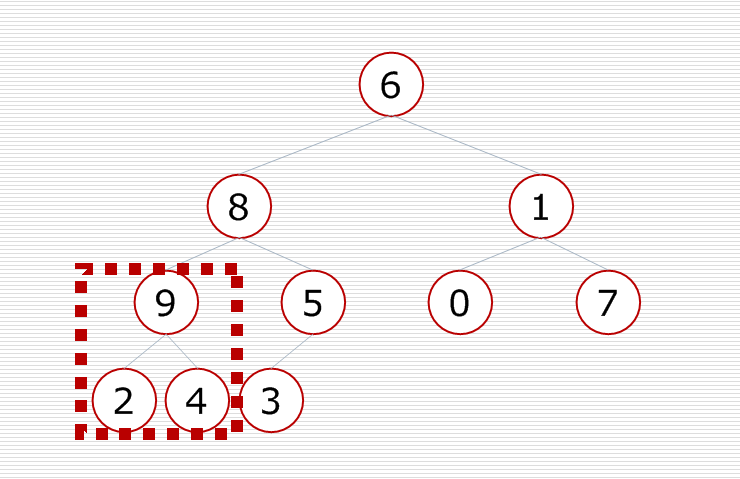
再对倒数第三个小子树进行调整,使这个小子树变成一个堆

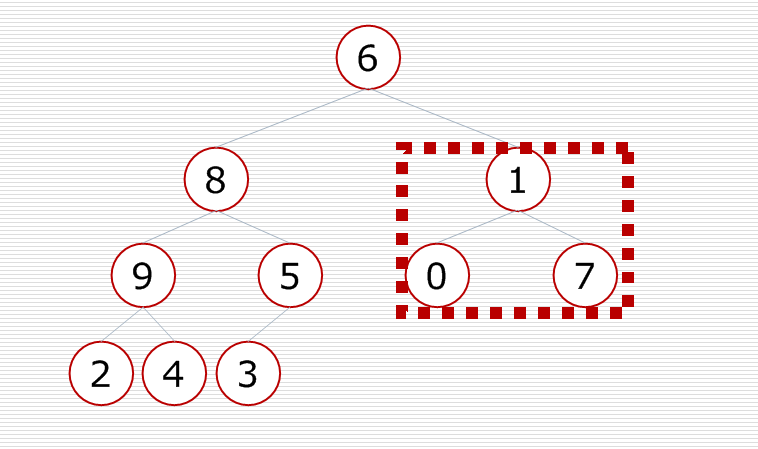
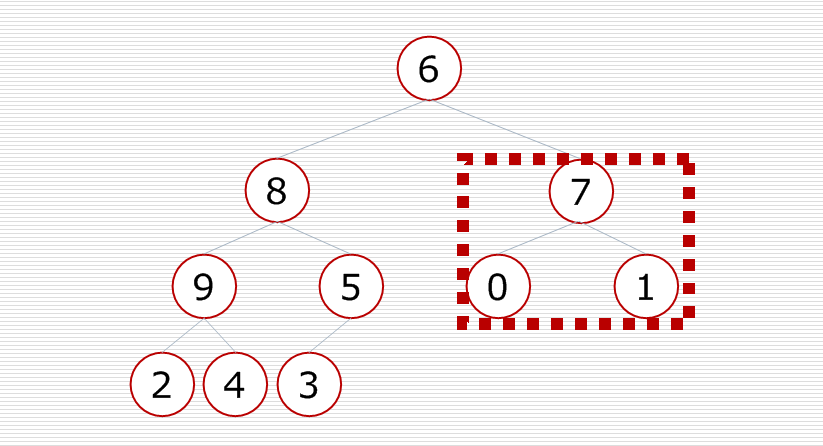
对这棵树中的每一个小子树都进行调整,最后这棵二叉树就变成了一个大根堆.

堆排序过程:

1.建立堆
2.得到堆顶元素,为最大元素
3.去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序
4.这时堆顶元素为堆中的第二大元素
5.重复3步骤,直到堆变空

代码实现:

def sift(li,left,right):
	i=left
	j= 2 *i +1
	tmp=li[left]

	while j <=right:
		if j < right and li[j] < li[j+1]:
			j += 1

		if tmp < li[j]:
			li[i] = li[j]
			i  = j
			j = 2 * i + 1
		else:
			break
	li[i] = tmp

def heap_sort(li):
	n = len(li)

	for i in range(n//2-1 , -1 ,-1):
		sift(li,i,n-1)
		print(li)

	for j in range(n-1,-1,-1):
		li[0],li[j]=li[j],li[0]
		sift(li,0,j-1)
		print(li)

li=[2,9,7,8,5,0,1,6,4,3]

sift(li,0,len(li)-1)

heap_sort(li)
print(li)

输出打印为:

[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[8, 6, 7, 4, 5, 0, 1, 2, 3, 9]
[7, 6, 3, 4, 5, 0, 1, 2, 8, 9]
[6, 5, 3, 4, 2, 0, 1, 7, 8, 9]
[5, 4, 3, 1, 2, 0, 6, 7, 8, 9]
[4, 2, 3, 1, 0, 5, 6, 7, 8, 9]
[3, 2, 0, 1, 4, 5, 6, 7, 8, 9]
[2, 1, 0, 3, 4, 5, 6, 7, 8, 9]
[1, 0, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

归并排序

把两段有序列表合并成一个有序列表

例如现在有列表li=[2,5,7,8,9,1,3,4,6]

1.这个列表以9为分割线,将列表分为两个部分,左边的部分[2,5,7,8,9]是一个有序列表,右边部分[1,3,4,6]也是一个有序列表
2.分别取这两段有序列表中的第一个元素,分别是2和1,由于1比2小,所以先把1排入一个新列表tmp中
3.再取右边部分的第二个元素3,3比2大,把2排入tmp中1元素的右边
4.再取左边部分的第二个元素5,5比3大,把3排入tmp中2元素右边
5.再取右男家部分的第三个元素4,再对4进行排序
6.直到这两段有序列表中的元素都排入tmp中,这时tmp就是li的有序状态

代码:

def merge(li, left, mid, right):
	i = left
	j = mid + 1

	ltmp = []

	while i <= mid and j <= right:
		if li[i] <= li[j]:
			ltmp.append(li[i])
			i += 1
		else:
			ltmp.append(li[j])
			j += 1

	while i <= mid:
		ltmp.append(li[i])
		i += 1

	while j <= right:
		ltmp.append(li[j])
		j += 1

	li[left:right + 1] = ltmp

def mergesort(li, left, right):
	if left < right:
		mid = (left + right) // 2
		mergesort(li, left, mid)
		mergesort(li, mid + 1, right)
		print(li[left:right + 1])

		merge(li, left, mid, right)
		print(li[left:right + 1])

li = [10, 4, 6, 3, 8, 2, 5, 7, 1, 9]

mergesort(li, 0, len(li) - 1)

print(li)

输出打印:

[10, 4]
[4, 10]
[4, 10, 6]
[4, 6, 10]
[3, 8]
[3, 8]
[4, 6, 10, 3, 8]
[3, 4, 6, 8, 10]
[2, 5]
[2, 5]
[2, 5, 7]
[2, 5, 7]
[1, 9]
[1, 9]
[2, 5, 7, 1, 9]
[1, 2, 5, 7, 9]
[3, 4, 6, 8, 10, 1, 2, 5, 7, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

归并排序将列表越分越小,直至分成一个元素,

一个元素是有序的

将两个有序列表归并,列表越来越大.

希尔排序

希乐排序是一种分组插入的排序算法

希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序

最后一次排序使得所有的数据有序

希尔排序代码:

def shell_sort(li):
	gap=len(li) //2
	while gap > 0:
		for i in range(gap,len(li)):
			tmp = li[i]
			j = i - gap
			while j >=0 and tmp < li[j]:

				li[j + gap] = li[j]
				j -=gap
			li[j + gap] = tmp
			print(li)

		gap /= 2

li=[10,4,6,3,8,2,5,7,1,9]

shell_sort(li)

print(li)

输出打印:

[2, 4, 6, 3, 8, 10, 5, 7, 1, 9]
[2, 4, 6, 3, 8, 10, 5, 7, 1, 9]
[2, 4, 6, 3, 8, 10, 5, 7, 1, 9]
[2, 4, 6, 1, 8, 10, 5, 7, 3, 9]
[2, 4, 6, 1, 8, 10, 5, 7, 3, 9]
[2, 4, 6, 1, 8, 10, 5, 7, 3, 9]
[2, 1, 6, 4, 8, 10, 5, 7, 3, 9]
[2, 1, 6, 4, 8, 10, 5, 7, 3, 9]
[2, 1, 6, 4, 8, 10, 5, 7, 3, 9]
[2, 1, 5, 4, 6, 10, 8, 7, 3, 9]
[2, 1, 5, 4, 6, 7, 8, 10, 3, 9]
[2, 1, 3, 4, 5, 7, 6, 10, 8, 9]
[2, 1, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 6, 7, 9, 8, 10]
[1, 2, 3, 4, 5, 6, 7, 9, 8, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]