『线段树 Segment Tree』

<更新提示>

<第一次更新> 更新了基础部分

<第二次更新>更新了\(lazytag\)标记的讲解

<正文>

线段树 Segment Tree

今天来讲一下经典的线段树。

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

简单的说，线段树是一种基于分治思想的数据结构，用来维护序列的区间特殊值，相对于树状数组，线段树可以做到更加通用，解决更多的区间问题。

性质

1.线段树的每一个节点都代表了一个区间
2.线段树是一棵二叉树，具有唯一的根节点，其中，根节点代表的是整个区间\([1,n]\)
3.线段树的每一个叶节点代表的是长度为\(1\)的元区间\([x,x]\)
4.对于每一个节点\([l,r]\)，它的左儿子被定义为\([l,mid]\)，右儿子被定义为\([mid+1,r]\)

如图，这就是一棵维护了区间\([1,10]\)的线段树。

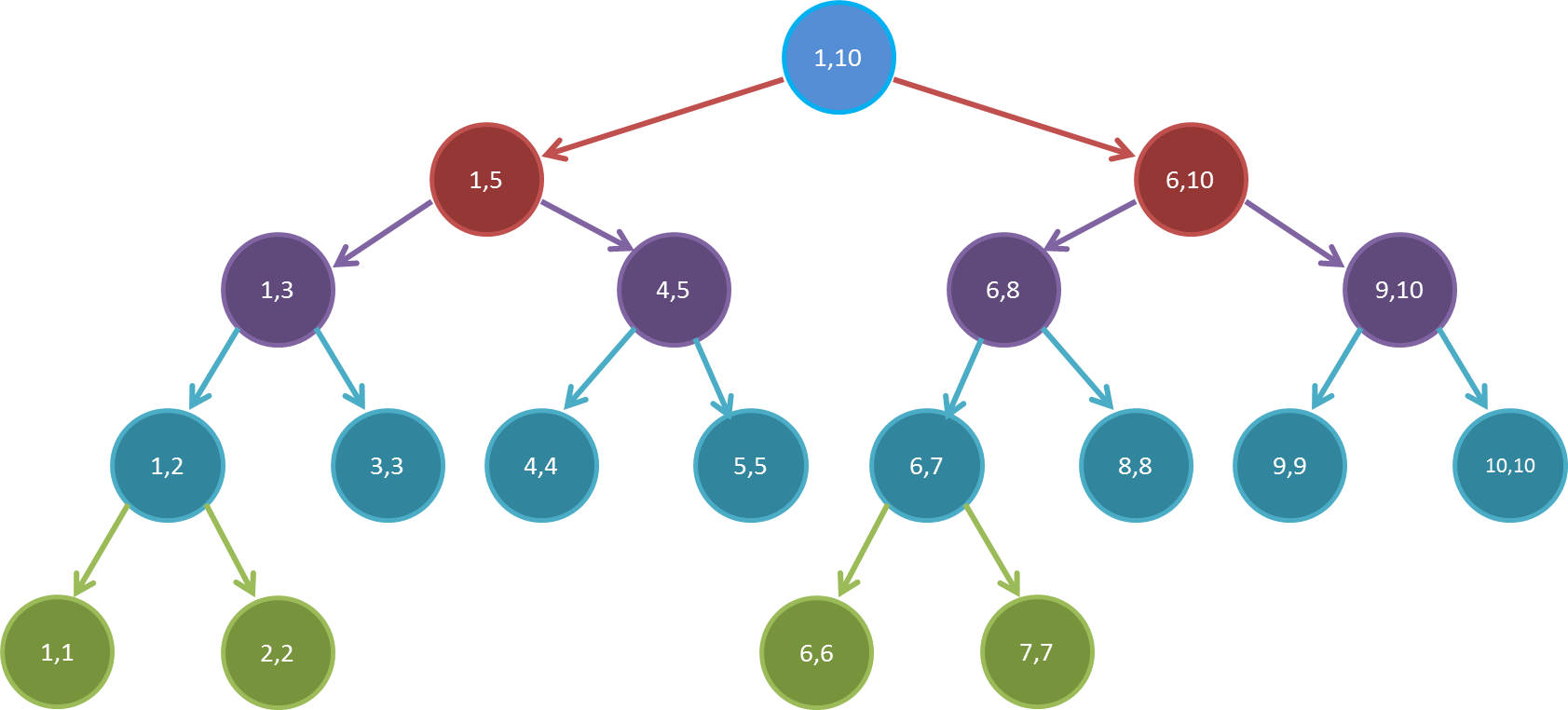
我们还可以发现，线段树层数为\(log_2n\)层，除去最后一层，线段树是一棵完全二叉树。

建树 (build)

我们来考虑一下如何储存并建立一棵线段树。

由于线段树是二叉树，所以我们可以直接用数组存储结点的编号，即对于节点\(x\)储存在\(a[p]\)处，我们令\(x\)的左儿子储存在\(a[p*2]\)处，右儿子储存在\(a[p*2+1]\)处，这样就可以快速地找到节点之间的父子关系。

理想状态下，\(n\)个叶节点的满二叉树有\((\sum_{i=0}^{2^i=n}2^i)=2n-1\)个节点，但由于最后一层至多还可能有\(2n\)个节点，所以数组空间要开到\(4n\)大小。

我们先来看一个维护区间最大值的例子。

对于线段树的每一个节点，我们可以额外的设置一个变量\(Max\)代表该节点所代表区间中的最大值，显然有:\(Max(p)=\max(Max(p*2),Max(p*2+1))\)，那么我们可以用如下方法建树。

\(Code:\)

struct SegmentTree

{

	int p,l,r,Max;

	#define l(x) tree[x].l

	#define r(x) tree[x].r

	#define p(x) tree[x].p

	#define Max(x) tree[x].Max

}tree[N*4];

inline void build(int p,int l,int r)//对于节点p，代表的区间为[l,r]

{

	l(p)=l,r(p)=r;//左右边界赋值

	if(l==r){Max(p)=0;return;}//如果为叶节点，直接赋值为权值

	int mid=(l+r)/2;

	//递归构建子树

	build(p*2,l,mid);

	build(p*2+1,mid+1,r);

	Max(p)=max(Max(p*2),Max(p*2+1));//回溯更新最大值

}

修改 (modify)

线段树支持节点的动态修改。

对于如 "将节点\(x\)修改权值为\(v\)" 的指令，线段树可以以自下向上的方式修改。具体地，可以从根节点作为入口进入，递归向下找到需要修改的节点，再在回溯过程中更新沿路祖先节点的最值信息。时间复杂度\(O(log_2n)\)。

\(Code:\)

inline void modify(int p,int x,int v)

{

	if(l(p)==r(p))//如果已经找到叶节点，更新权值

	{

		Max(p)=v;

		return;

	}

	int mid=(l(p)+r(p))/2;

	if(x<=mid)modify(p*2,x,v);//如果在左子树中，则递归左子树寻找

	if(x>mid)modify(p*2+1,x,v);//如果在右子树中，则递归右子树寻找

	Max(p)=max(Max(p*2),Max(p*2+1)); //回溯更新

}

查询 (query)

线段树还需要能够解决区间最值查询问题。

对于如 "查询区间\([l,r]\)的最大值" 的指令，线段树可以递归查找得到最大值。具体地，从根节点开始，递归执行以下过程：

1.若\([l,r]\)完全覆盖了当前结点所代表的区间，返回当前结点区间中的最大值作为备选答案
2.若左子节点与\([l,r]\)有重合部分，递归访问左子节点
3.若右子节点与\([l,r]\)有重合部分，递归访问右子节点

可以证明，区间查询的时间复杂度至多为\(O(2log_2n)\)。

\(Code:\)

inline int query(int p,int l,int r)

{

	if(l<=l(p)&&r>=r(p))return Max(p);//如果完全包含这个区间，返回这个区间的最大值作为备选答案

	int mid=(l(p)+r(p))/2;

	int res=-INF;

	//递归查询有重合部分的左右区间

	if(l<=mid)res=max(res,query(p*2,l,r));

	if(r>mid)res=max(res,query(p*2+1,l,r));

	return res;

}

至此，线段树的基本模型已经构成，我们通过一道模板题展示一下代码。

Description

给定一个包含n个数的序列，初值全为0，现对这个序列有两种操作：

操作1：把给定第k1 个数改为k2;

操作2：查询从第k1个数到第k2个数得最大值。（k1<=k2<=n）

所有的数都 <=100000

Input Format

第一行给定一个整数n，表示有n个操作。

以下接着n行，每行三个整数，表示一个操作。

第一个树表示操作序号，第二个数为k1，第三个数为k2

Output Format

若干行，查询一次，输出一次。

Sample Input

Sample Output

\(Code:\)

#include<bits/stdc++.h>

using namespace std;

const int N=100000+200,INF=0x3f3f3f3f;

int n;

struct SegmentTree

{

	int p,l,r,Max;

	#define l(x) tree[x].l

	#define r(x) tree[x].r

	#define p(x) tree[x].p

	#define Max(x) tree[x].Max

}tree[N*4];

inline void build(int p,int l,int r)

{

	l(p)=l,r(p)=r;

	if(l==r){Max(p)=0;return;}

	int mid=(l+r)/2;

	build(p*2,l,mid);

	build(p*2+1,mid+1,r);

	Max(p)=max(Max(p*2),Max(p*2+1));

}

inline void modify(int p,int x,int v)

{

	if(l(p)==r(p))

	{

		Max(p)=v;

		return;

	}

	int mid=(l(p)+r(p))/2;

	if(x<=mid)modify(p*2,x,v);

	if(x>mid)modify(p*2+1,x,v);

	Max(p)=max(Max(p*2),Max(p*2+1));

}

inline int query(int p,int l,int r)

{

	if(l<=l(p)&&r>=r(p))return Max(p);

	int mid=(l(p)+r(p))/2;

	int res=-INF;

	if(l<=mid)res=max(res,query(p*2,l,r));

	if(r>mid)res=max(res,query(p*2+1,l,r));

	return res;

}

inline void input(void)

{

	scanf("%d",&n);

	build(1,1,n);

}

inline void solve(void)

{

	for(int i=1;i<=n;i++)

	{

		int index,k1,k2;

		scanf("%d%d%d",&index,&k1,&k2);

		if(index==1)modify(1,k1,k2);

		else printf("%d\n",query(1,k1,k2));

	}

}

int main(void)

{

	input();

	solve();

	return 0;

}

延迟标记 (lazytag)

在实现了简单的线段树后，我们考虑一下拓展。

我们以上实现的线段树是支持区间查询和单点修改的，如果需要区间修改呢？

如果用之前的线段树直接做的话，每一次修改的时间复杂度是\(O(log_2n)\)，那么区间修改的时间复杂度将会达到至多\(O(nlog_2n)\)，这是我们无法承受的。

我们可以考虑一下这种情况:对于一次区间修改指令\([l,r,delta]\)(将\([l,r]\)内的所有元素加\(delta\))，如果在之后的区间询问中完全没有调用到区间\([l,r]\)，那么这次\(O(nlog_2n)\)的修改就是完全无用的。

这样，我们对于每一个线段树中的节点引入一个变量\(lazytag\)延迟标记，\(lazytag(x)\)代表\(x\)被已经某一次区间操作修改，但是\(x\)的子节点暂时还未修改，其修改的变化量为\(lazytag(x)\)。然后，我们对于每一个区间修改操作，只对一个点做更新，并修改其\(lazytag\)值。需要查询时，我们再下传\(lazytag\)标记，顺带更新每一个沿路节点的关键值，就可以保证查询可以得到正确答案。

那么，每一次区间修改操作就只需要对\(log_2n\)个节点做修改，时间复杂度就优化到了\(O(log_2n)\)，对于子节点的更新，只需要在查询时顺带更新即可。

\(Code:\)

struct SegmentTree

{

	int p,l,r,Max,lazytag;

	#define l(x) tree[x].l

	#define r(x) tree[x].r

	#define p(x) tree[x].p

	#define Max(x) tree[x].Max

	#define lazytag(x) tree[x].lazytag

}tree[N*4];

inline void spread(int p)

{

	if(lazytag(p))//将有标记节点的子节点更新，并下传标记

	{

		Max(p*2)+=lazytag(p);

		Max(p*2+1)+=lazytag(p);

		lazytag(p*2)+=lazytag(p);

		lazytag(p*2+1)+=lazytag(p);

		lazytag(p)=0;

	}

}

inline void modify(int p,int l,int r,int d)

{

	if(l<=l(p)&&r>=r(p))//包含修改区间，进行标记

	{

		Max(p)+=d;

		lazytag(p)+=d;

		return;

	}

	spread(p);//下传标记

	int mid=(l(p)+r(p))/2;

	if(l<=mid)modify(p*2,l,r,d);

	if(r>mid)modify(p*2+1,l,r,d);

	Max(p)=max(Max(p*2),Max(p*2+1));

}

inline int query(int p,int l,int r)

{

	if(l<=l(p)&&r>=r(p))return Max(p);

	spread(p); //下传标记

	int mid=(l(p)+r(p))/2;

	int res=-INF;

	if(l<=mid)res=max(res,query(p*2,l,r));

	if(r>mid)res=max(res,query(p*2+1,l,r));

	return res;

}

通过一道例题展示一下区间修改线段树的代码。

Description

给定一个包含n个数的序列，初值全为0，现对这个序列有两种操作：

操作1：将第k1 个数到第k2 个数加1；

操作2：查询从第k1个数到第k2个数得最大值。（k1<=k2<=n）

所有的数都 <=100000

Input Format

第一行给定一个整数n，表示有n个操作。

以下接着n行，每行三个整数，表示一个操作。

Output Format

若干行，查询一次，输出一次。

Sample Input

Sample Output

\(Code:\)

#include<bits/stdc++.h>

using namespace std;

const int N=100000+200,INF=0x3f3f3f3f;

int n;

struct SegmentTree

{

	int p,l,r,Max,lazytag;

	#define l(x) tree[x].l

	#define r(x) tree[x].r

	#define p(x) tree[x].p

	#define Max(x) tree[x].Max

	#define lazytag(x) tree[x].lazytag

}tree[N*4];

inline void build(int p,int l,int r)

{

	l(p)=l,r(p)=r;

	if(l==r){Max(p)=0;return;}

	int mid=(l+r)/2;

	build(p*2,l,mid);

	build(p*2+1,mid+1,r);

	Max(p)=max(Max(p*2),Max(p*2+1));

}

inline void spread(int p)

{

	if(lazytag(p))

	{

		Max(p*2)+=lazytag(p);

		Max(p*2+1)+=lazytag(p);

		lazytag(p*2)+=lazytag(p);

		lazytag(p*2+1)+=lazytag(p);

		lazytag(p)=0;

	}

}

inline void modify(int p,int l,int r,int d)

{

	if(l<=l(p)&&r>=r(p))

	{

		Max(p)+=d;

		lazytag(p)+=d;

		return;

	}

	spread(p);

	int mid=(l(p)+r(p))/2;

	if(l<=mid)modify(p*2,l,r,d);

	if(r>mid)modify(p*2+1,l,r,d);

	Max(p)=max(Max(p*2),Max(p*2+1));

}

inline int query(int p,int l,int r)

{

	if(l<=l(p)&&r>=r(p))return Max(p);

	spread(p);

	int mid=(l(p)+r(p))/2;

	int res=-INF;

	if(l<=mid)res=max(res,query(p*2,l,r));

	if(r>mid)res=max(res,query(p*2+1,l,r));

	return res;

}

inline void input(void)

{

	scanf("%d",&n);

	build(1,1,n);

}

inline void solve(void)

{

	for(int i=1;i<=n;i++)

	{

		int index,k1,k2;

		scanf("%d%d%d",&index,&k1,&k2);

		if(index==1) modify(1,k1,k2,1);

		else printf("%d\n",query(1,k1,k2));

	}

}

int main(void)

{

	input();

	solve();

	return 0;

}

<后记>