Apriori算法-频繁项集-关联规则

计算频繁项集：

首先生成一个数据集

def loadDataSet():
    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

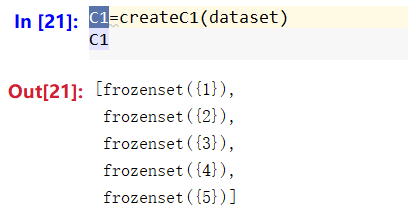
测试数据集dataset有了，第一步，我们要根据数据集dataset得到一个集合C1，集合C1中包含的元素为dataset的无重复的每个单元素，候选项集。

def createC1(dataset):
    C1 = []
    for transaction in dataset:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()
    return map(frozenset, C1)

返回的数据map计算得到一个元素为frozenset的集合。

为什么要转成frozenset?

原因两个：

1.  这个集合是从dataset中抽取出所有无重复的数据集，是固定的，应该是不可变的类型。

2.  frozenset可以作字典

可以看一下返回结果：

第二步，计算C1<key>每个元素key的支持度。

       支持度= count(key) / sizeof(C1)

def scanD(D, Ck, minSupport):
    ssCnt = {}
    for tid in D:
        for can in Ck:
            if can.issubset(tid):
                if not ssCnt.has_key(can):
                    ssCnt[can] = 1
                else:
                    ssCnt[can] += 1
    numitems = float(len(D))  # 数据集长度
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key] / numitems
        if support >= minSupport:
            retList.insert(0, key)
        supportData[key] = support
    return retList, supportData

调用返回结果：

先把dataset转成元素为集合的类型。

这里设置支持度为0.5。当key在dataset中出现的集合个数超过一半即认为是频繁项。

L1是根据计算C1中每个元素是否满足支持度规则过滤得到的C1的子集。

L1的元素两两组合构成C2，再根据C2中每个元素是否满足支持度规则过滤得到的C1的子集L2。依次类推，直到Lk是单元素集合。

添加如下代码，可以得到一个完整的找频繁项集的代码：

def aprioriGen(Lk, k):
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            L1 = list(Lk[i])[:k - 2];
            L2 = list(Lk[j])[:k - 2]
            L1.sort()
            L2.sort()
            if L1 == L2:
                retList.append(Lk[i] |
Lk[j])
    return retList
def apriori(dataset, minsupport=0.5):
    C1 = createC1(dataset)  # 候选项集
    D = map(set, dataset)  # 数据集
    L1, supportData =
scanD(D, C1, minsupport)  # 频繁项集与支持度
    L = [L1]
    k = 2
    while (len(L[k - 2]) > 0):
        Ck = aprioriGen(L[k - 2], k)
        Lk, supK = scanD(D, Ck,
minsupport)
        supportData.update(supK)
        L.append(Lk)
        k += 1
    return L, supportData

apriori是主函数，这里对Lk进行了合并，如果Lk的两个元素（都是集合，假设分别是Lk1,Lk2）的[0:k-2]是一样的，（k是什么？k是Lk1的长度加1）比方说：

example1:

{a},{c} k=2    

[0:k-2]分别是{}=={}，需要进行合并。得到{a,c}

注意：[0:0]意思是从0开始取（含0），直到0（不含0），所以是{}

example2:

{a,c},{a,d}   k=3

[0:k-2]分别是{a}=={a}，合并得到{a,c,d}

注意：[0:1]意思是从0开始取（含0），直到1（不含1），所以是{a}

应该能理解怎么合并的了。

为什么要合并？

上面解释了怎么合并，以及合并的规则。我们拿到的数据是由C1生成的L1，L1是单元素中符合支持度的构成的集合。所以我们只需要对L1进行组合，就能得到二元素集合C2，并根据支持度过滤得到其中符合支持度的二元素的频繁项集L2。由L1得到C2，这就是为什么要合并的理由。

为什么用这种合并规则呢？

L1={[frozenset([1]), frozenset([3]),

        frozenset([2]), frozenset([5])]}

很明显，我们可以组合得到

Ck[k=2]={[frozenset([1, 3]), frozenset([1, 2]), frozenset([1, 5]), frozenset([2, 3]), frozenset([3, 5]), frozenset([2, 5])]}

scanD(D, Ck, minsupport)执行该函数得到我们想要的

Lk[k=2]= {[frozenset([1, 3]), frozenset([2, 5]), frozenset([2, 3]), frozenset([3, 5])]}。

接着看：

接下来我们就要对Lk[k=2]进行组合了。按照我们的规则：

[1,3]没有与之可以合并的。

[2,5][2,3]可以合并。得到[2,3,5]

[3,5]没有与之合并的。

所以Ck[k=3]={[frozenset([2, 3, 5])]}

假如我们不按照该规则来：

[1,3][2,5]=>[1,2,3,5]，三元素集合这点规则是必须要遵守的。

[1,3][2,3]=>[1,2,3]出现[1,2]该子集不满足支持度。

[1,3][3,5]=>[1,3,5]出现[1,5]该子集不满足支持度。

[2,5][2,3]=>[2,3,5]

[2,5][3,5]=>[2,3,5]

[2,3][3,5]=>[2,3,5]出现三个重复的[2,3,5]，还需要我们添加去重规则，相对比较麻烦。而且按照我们的规则，可以减少集合的数目，省去遍历去重的过程，降低算法的时间复杂度。

根据规则生成的Ck，是建立在不违背最小支持度的基础之上的，至于生成的Ck是否符合最小支持度，接下来要使用scanD算法来进行验证，并丢掉不符合最小支持度的项集。

有一个问题：

k-2的操作，到底是怎么做到的，避免出现类似[1,2,3]这种含有[1,2]子集是之前已经被抛弃的集合。还是说，这里就是一个巧合？。

挖掘关联规则：

1.  # 下面是关联规则   默认最小置信度为0.7

2.  # 主函数

3.  def generateRules(L, supportData, minConf=0.7):

4.      bigRuleList = []

5.      for i in range(1, len(L)):  # 不处理单元素集合L[0]

6.          for freqSet in L[i]:

7.              H1 = [frozenset([item]) for item in freqSet]

8.              if (i > 1):  # 当集合中元素的长度大于2的时候，尝试对集合合并。

9.                  # 比如：[2,3,5]=>{[2,3],5}

10.                ŒrulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)

11.            else:  # 对于2元组，直接计算置信度

12.                calConf(freqSet, H1, supportData, bigRuleList, minConf)

13.    return bigRuleList

14.

15.

16.def calConf(freqSet, H, supportData, brl, minConf=0.7):

17.    prunedH = []

18.    for conseq in H:

19.        conf = supportData[freqSet] / supportData[freqSet - conseq]  # 置信度

20.        if conf >= minConf:

21.            print freqSet - conseq, "--->", conseq, "conf", conf

22.            brl.append((freqSet - conseq, conseq, conf))

23.            prunedH.append(conseq)

24.        if (len(freqSet) > 2):

25.            conf = supportData[freqSet] / supportData[conseq]  # 置信度

26.            if conf >= minConf:

27.                print conseq, "--->", freqSet - conseq, "conf", conf

28.                brl.append((conseq, freqSet - conseq, conf))

29.                prunedH.append(freqSet - conseq)

30.    return prunedH

31.

32.

33.def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):

34.    m = len(H[0])

35.    if (len(freqSet) > (m + 1)):

36.        Hmp1 = aprioriGen(H, m + 1)

37.        Hmp1 = calConf(freqSet, Hmp1, supportData, brl, minConf)

38.        if (len(Hmp1) > 1):

39.            rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)

40.

41.

42.ruleList = generateRules(L, supportData)

43.# print ruleList

对rulesFromConseq解释一下：

在主函数generateRules中的Œ标记处，此时freqSet是三元组[2,3,5]，尝试对其元素进行合并。调用rulesFromConseq，执行aprioriGen(H, m + 1)得到Hmp1={[frozenset([2, 3]), frozenset([2, 5]),

               frozenset([3, 5])]}

然后调用calConf计算置信度。

这里对calConf补充了如下代码：

1.          if (len(freqSet) > 2):

2.              conf = supportData[freqSet] / supportData[conseq]  # 置信度

3.              if conf >= minConf:

4.                  print conseq, "--->", freqSet - conseq, "conf", conf

5.                  brl.append((conseq, freqSet - conseq, conf))

6.                  prunedH.append(freqSet - conseq)

理由：原代码，如果freqSet =[2,3,5] H={[frozenset([2, 3]), frozenset([2, 5]), frozenset([3, 5])]}

[2,3,5]去计算对[2][3][5]的置信度均不符合最小要求，返回[]，无法继续对[2,3][2,5][3,5]进行置信度验证。

源代码：https://files.cnblogs.com/files/simuhunluo/Apriori%E7%AE%97%E6%B3%95%E4%BB%A3%E7%A0%81.zip