[Luogu 3902]Increasing

Description

Input

Output

Sample Input

3
1 3 2

Sample Output

1

HINT

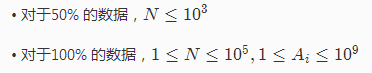
题解

由于题目要求我们求严格递增的数列，即：

$$A[i]>A[i-1],1<i<=N$$

我们不妨令B[i]=A[i]-i，那么我们容易得到

$$B[i]>=B[i-1],1<i<=N$$

两式是等价的。

那么我们可以将原数列处理一下，我们只需要求出$B[i]$的最长不下降子序列，把不在序列中的那些数$B[i]$都改成符合条件的数（比如说和左边最近一个在最长不下降子序列中的$B[j]$相等）就能满足题意了。

当然，我们并不需要求出具体的修改方案，我们只需要求出最长不下降的长度$K$，输出$N-K$即可。

注意：

由于数据为$10^5$显然我们要用二分优化求最长不下降子序列长度。同时由于减去了$i$，我们需要将数组初始化为极小值。

 #include<map>
 #include<set>
 #include<ctime>
 #include<cmath>
 #include<queue>
 #include<stack>
 #include<cstdio>
 #include<string>
 #include<vector>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #define LL long long
 #define RE register
 #define IL inline
 using namespace std;
 const int N=1e5;

 int n,x;
 int f[N+],maxn;

 IL int Dev(int x)
 {
     int l=,r=maxn,mid,ans;
     while(l<=r)
     {
         mid=(l+r)>>;
         if (f[mid]<=x) ans=mid,l=mid+;
         else r=mid-;
     }
     return ans;
 }
 IL int Min(int a,int b) {return a<b ? a:b;}

 int main()
 {
     memset(f,,sizeof(f));
     scanf("%d",&n);
     for (RE int i=;i<=n;i++)
     {
         scanf("%d",&x);
         x-=i;
         int tmp=Dev(x);
         if (tmp==maxn) f[++maxn]=x;
         else f[tmp+]=Min(f[tmp+],x);
     }
     printf("%d\n",n-maxn);
     return ;
 }