HASH方法课下补分博客

课堂要求：利用除留余数法为下列关键字集合的存储设计hash函数，并画出分别用开放寻址法和拉链法解决冲突得到的空间存储状态（散列因子取0.75）关键字集合：85，75，57，60，65，（你的8位学号相加值），98，74，89，12，5，46，97，13，69，52，92。完成计算并提交计算过程。

实践要点：通过课上对hash方法以及散列函数的学习，了解散列冲突的机制，并学习解决散列冲突的方法。主要学习和实践的方法是开放地址法和拉链法，首先需要理解这两种方法的实现过程，然后运用到实际的题目中去解决问题。

散列函数的构造：

散列函数的选择有两条标准：简单和均匀简单指散列函数的计算简单快速；

均匀指对于关键字集合中的任一关键字，散列函数能以等概率将其映射到表空间的任何一个位置上。也就是说，散列函数能将子集k随机均匀地分布在表的地址集{0，1，…，m-1}上，以使冲突最小化。

实验过程：首先是开放地址法

1.基本思想：在散列表中形成一个探查序列，沿此序列逐单元进行查找，直到找到一个空的单元时将新结点放入。当发生地址冲突后，求解下一个地址用:ND =( D+di)%m i=1,2,…,k(k<= m-1)；关于开放地址法的key值问题：H i ( key ) = ( H ( key )+ d i ) mod m ( i = 1,2,…… ， k ( k ≤ m – 1)) ，其中： H ( key ) 为关键字 key 的直接哈希地址， m 为哈希表的长度， di 为每次再探测时的地址增量。

采用这种方法时，首先计算出元素的直接哈希地址 H ( key ) ，如果该存储单元已被其他元素占用，则继续查看地址为 H ( key ) + d 2 的存储单元，如此重复直至找到某个存储单元为空时，将关键字为 key 的数据元素存放到该单元。

对应到题目中的内容：首先是关键字集合，85，75，57，60，65，（你的8位学号相加值），98，74，89，12，5，46，97，13，69，52，92，学号为20162309，则累加学号为23，则关键字集合为85，75，57，60，65，23，98，74，89，12，5，46，97，13，69，52，92。因为长度为17，散列因子为0.75，则计算出的n值为23（实际为22.667），距离其最近的且不大于23的最小质数为19，本题也可以用key值除以23.

则可以得到散列函数为： H(key)=key%23

结合散列地址的计算方法，相同余数后进一位法则，得到散列表的储存空间状态。在散列地址的求解中，共有四个关键字余数为0，则按照从大到小的顺序依次占据了散列地址的前四个位置。

由此可以列出散列图：

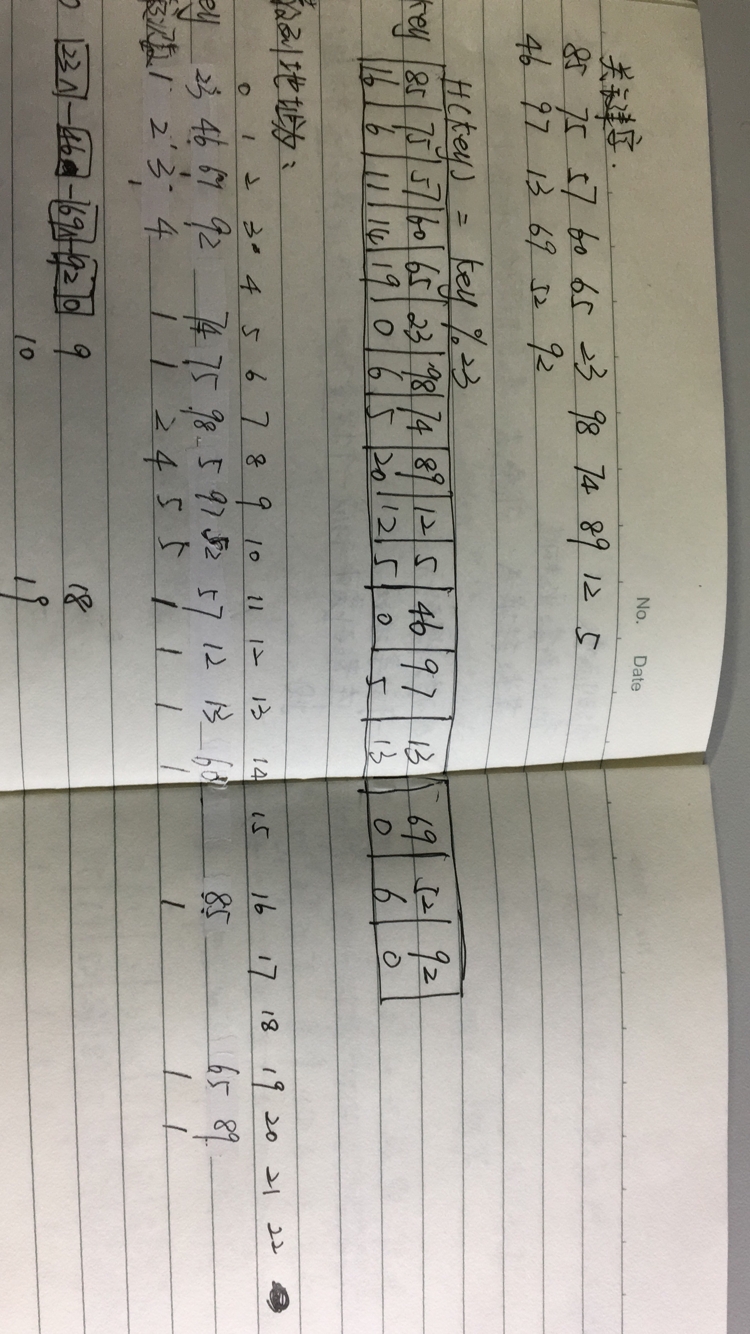
相关开发地址法的信息补充：

开放地址法的双散列法，是另一种开放地址的取值方法，首先使用第一个散列函数H1(key)及逆行那个散列，一旦发生冲突，则使用第二个函数H2(key)计算改项到达下一个存储地址的增量，其取值p和key有关，范围在1和m之间，并且与m互质的正整数。

双散列的取值自然需要两个key值，可取D = H1(key);p = H2(key);则ND = (D+p)%m。

哈希方法下的元素删除问题：删除的数据所在位置需做标记，对利用开放地址法查了冲突所产生的哈希表中删除一个元素，不能简单地直接删除，因为这样将截断其它具有相同哈希地址的元素的查找地址，所以应设定一个特殊的标志以表明该元素已被删除。

第二个方法是拉链法：

1.基本思想：拉链法解决冲突的做法是：将所有关键字为同义词的结点链接在同一个单链表中。若选定的散列表长度为m，则可将散列表定义为一个由m个头指针组成的指针数组t[0..m-1]。凡是散列地址为i的结点，均插入到以t为头指针的单链表中。t中各分量的初值均应为空指针。在拉链法中，装填因子α可以大于1，但一般均取α≤1。

如果拉链法没有出现堆积，则可以直接删除。

具体到题目上，因为已经得到了散列地址和储存空间，则拉链法的图就比较容易得到了。

则：

拉链法需要列出重复的量，且要按进入的顺序列出。