[Codeforces]663E Binary Table

　　某变换好题。不过听说还有O(2^n*n^2)DP的……

Description

　　给定一个n*m的01矩阵，你可以选择对任意行和任意列取反，使得最终“1”的数量尽量少。

Input

　　第一行两个整数n,m。
　　接下来n行，每行m个字符，描述一个01矩阵。

Output

　　一个整数表示最少的1的数量。

Sample Input

　　3 4
　　0110
　　1010
　　0111

Sample Output

　　2

HINT

　　1 <= n <= 20，1 <= m <= 100000。

Solution

　　首先发现矩阵只有20行，经过一番脑补，可以把这二十行压成一个数。

　　然后我们就得到了m个数。

　　然后在行上的取反就相当于将这m个数同时异或上同一个数。

　　然后我们要求的就是，找出一个数，使得这m个数同时异或上这个数后，每个数的二进制位中的0和1的个数的最小值总和最小。

　　我们设ans[x]为当异或的数为x时的答案，a数组用来存放m个数，d[x]为x的二进制位中0和1的个数的最小值。

　　所以：

　　　　，

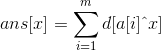　　我们稍微改一改，用w[x]表示在m个数中，为x的数有多少个：

　　　　。

　　等等，是不是发现了什么？这不就是卷积FWT的式子吗？

　　　　。

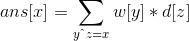　　时间复杂度O(nm+2^n*n)。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define MS 23
#define MN 100005
#define MM 1100005
using namespace std;
char c[MS][MN];
int a[MN];
ll A[MM],B[MM],C[MM];
int n,m,ans;

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

void FWT(ll* a,int len,bool g)
{
    register int wt,st,i;
    ll x,y;
    for (wt=;wt<len;wt<<=)
        for (st=;st<len;st+=wt<<)
            for (i=;i<wt;++i)
            {
                x=a[st+i]; y=a[st+wt+i];
                a[st+i]=x+y; a[st+wt+i]=x-y;
                if (g) a[st+i]>>=,a[st+wt+i]>>=;
            }
}

int main()
{
    register int i,j;
    n=read(); m=read(); ans=n*m;
    for (i=;i<n;++i) scanf("%s",c[i]+);
    for (i=n-;i>=;--i)
        for (j=;j<=m;++j) a[j]=(a[j]<<)+c[i][j]-'';
    for (i=;i<=m;++i) ++A[a[i]];
    for (i=;i<(<<n);++i) B[i]=B[i>>]+(i&);
    for (i=;i<(<<n);++i) B[i]=min(B[i],n-B[i]);
    FWT(A,<<n,false); FWT(B,<<n,false);
    for (i=;i<(<<n);++i) C[i]=A[i]*B[i];
    FWT(C,<<n,true);
    for (i=;i<(<<n);++i) ans=min(ans,(int)C[i]);
    printf("%d",ans);
}

Last Word

　　如果把FWT中的if语句改成(x+y)/g，(x-y)/g，效率会慢5倍，除法真是个可怕的东西。