计蒜客NOIP模拟赛(2) D1T2 表演艺术

凡和邻家男孩玩完了纸牌，兴致很高，于是准备了一场表演艺术对抗赛。他特意请来了很多表演艺术家，分成绿黑两队，进行名为 PK，实则捞金的表演。

凡为了捞金，开设了一个赌局，在比赛开始之前招揽人们来押注谁能胜出，在所有人进行投注之后，凡需要告诉大家绿方和黑方的单位返还金额都是多少。

举个例子，如果绿方的单位返还金额为 555，那么我每押 111 块钱绿方胜，如果成真就能拿回 555 块钱，但是如果结果绿方输了，我就拿不回来任何钱。

凡决定将单位返还金额设得更具有吸引力，所以他要求“绿方胜的单位返还金额+黑方胜的单位返还金额=T”，并且为了赚更多的钱，凡可以在中间某两个投注的人之间更改单位返还金额，但是要求双方的总和仍然为 T，并且只能更改一次。

不幸的是，凡突然发现自己请来的表演艺术家竟然和众多投注人是一伙的，也就是说，在凡定下单位返还金额之后，那些艺术家会操纵比赛结果，从而让凡拿出更多的钱来。

这下凡有些慌了，于是他来询问你应该怎么制定单位返还金额。

输入格式

第一行一个整数 NNN，代表投注的人的个数。

接下来 NNN 行，每行两个实数 ai,bia_i,b_iai,bi 代表第 iii 个人投注黑方胜和绿方胜的资金。

最后一行一个实数 TTT，含义如题目中所示。

输出格式

一个实数，代表你最少返还的金额(保留两位小数)。

数据范围与约定

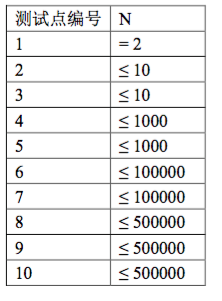
对于所有数据，0≤ai,bi,T≤1000\le a_i,b_i,T \le 1000≤ai,bi,T≤100，且至多精确到两位小数。

样例解释 1

一种最优方案是:

第一次投注及之前，单位返还金额为 101010 和 000。

第二次投注及之后，单位返还金额为 000 和 101010

这样无论哪方胜利，你都不会返还任何金钱。

样例解释 2

一种最优方案是:

第一次投注及之前，单位返还金额为 0.50.50.5 和 0.50.50.5。

第二次投注及之后，单位返还金额为 0.50.50.5 和 0.50.50.5

这样无论哪方胜利,你的返还金额都为 555。

样例输入1

样例输出1

0.00

样例输入2

样例输出2

5.00
题解：
因为无论如何都是最差情况,所以让两方胜利之后返还金额相等是最好的
先枚举在哪里分段,设分段之前押黑方胜的资金为 A,绿方胜资金为 C,之后押黑方胜资金为 B,绿方胜资金为 D,分段之前黑方胜单位返还金额为 p,分
段之后为 q,则有式子:(A+C)p+(B+D)q=(C+D)T
在满足上述式子的前提下要求 Ap+Bq 最小
稍作分析可知q，p值在某一个极值最优，意思是：要么p尽可能大，要不q尽可能大

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<cmath>

 using namespace std;

 double a[],b[],tota,totb,A,B,C,D,p,q,T,ans=2e9;

 int n;

 int main()

 {int i;

   cin>>n;

   for (i=;i<=n;i++)

     {

       scanf("%lf%lf",&a[i],&b[i]);

       if (a[i]<=1e-&&b[i]<=1e-) n--,i--;

       tota+=a[i];totb+=b[i];

     }

    cin>>T;

    A=;B=tota;C=;D=totb;

    for (i=;i<n;i++)

      {

        A+=a[i];B-=a[i];C+=b[i];D-=b[i];

        if (A<=D) p=T;

        else p=T*(C+D)/(A+C);

        q=(T*(C+D)-(A+C)*p)/(B+D);

        if (A*p+B*q<ans) ans=A*p+B*q;

        if (B<=C) q=T;

        else q=T*(C+D)/(B+D);

        p=(T*(C+D)-(B+D)*q)/(A+C);

        if (A*p+B*q<ans) ans=A*p+B*q;

      }

    printf("%.2lf",ans);

 }