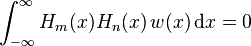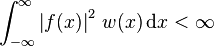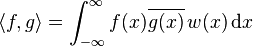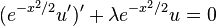数值分析:Hermite多项式
http://blog.csdn.net/pipisorry/article/details/49366047
Hermite埃尔米特多项式
在数学中,埃尔米特多项式是一种经典的正交多项式族,得名于法国数学家夏尔·埃尔米特。概率论里的埃奇沃斯级数的表达式中就要用到埃尔米特多项式。在组合数学中,埃尔米特多项式是阿佩尔方程的解。物理学中,埃尔米特多项式给出了量子谐振子的本征态。
前4个(概率论中的)埃尔米特多项式的图像
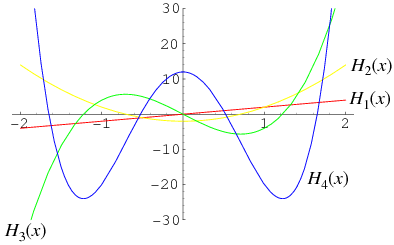
The Hermite polynomials 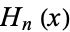 are set of orthogonal polynomials over the domain
are set of orthogonal polynomials over the domain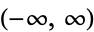
with weighting function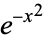 , illustrated above for
, illustrated above for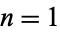 ,
,
2, 3, and 4. Hermite polynomials are implemented in the Wolfram Language asHermiteH[n,x].
The Hermite polynomial 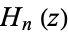 can be defined by the contour integral
can be defined by the contour integral
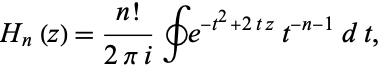 |
(1)
|
where the contour encloses the origin and is traversed in a counterclockwise direction (Arfken 1985, p. 416).
Hermite多项式,其正交域为(-∞, +∞),其一维形式是
其中,Hk(x)前面的乘式为正交归一化因子,为计算简便可省略。
前10个Hermite多项式
H_0(x) =
1
H_1(x) =
2x
H_2(x) =
4x^2-2
H_3(x) =
8x^3-12x
H_4(x) =
16x^4-48x^2+12
H_5(x) =
32x^5-160x^3+120x
H_6(x) =
64x^6-480x^4+720x^2-120
H_7(x) =
128x^7-1344x^5+3360x^3-1680x
H_8(x) =
256x^8-3584x^6+13440x^4-13440x^2+1680
H_9(x) =
512x^9-9216x^7+48384x^5-80640x^3+30240x
H_(10)(x) =
1024x^(10)-23040x^8+161280x^6-403200x^4+302400x^2-30240
The values 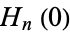 may be called Hermite numbers.When ordered from smallest to largest powers, the triangle
may be called Hermite numbers.When ordered from smallest to largest powers, the triangle
of nonzero coefficientsis 1; 2; -2, 4; -12, 8; 12, -48, 16; 120, -160, 32; ... (OEISA059343).
Hermite多项式的性质
多项式Hn 是一个n次的多项式。概率论的埃尔米特多项式是首一多项式(最高次项系数等于1),而物理学的埃尔米特多项式的最高次项系数等于2n。
正交性
多项式Hn 的次数与序号n 相同,所以不同的埃尔米特多项式的次数不一样。对于给定的权函数w,埃尔米特多项式的序列将会是正交序列。
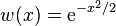 (概率论)
(概率论)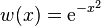 (物理学)
(物理学)
也就是说,当m ≠ n 时:
除此之外,还有:

(概率论)
(物理学)
其中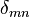 是克罗内克函数。
是克罗内克函数。
从上式可以看到,概率论中的埃尔米特多项式与标准正态分布正交。
完备性
在所有满足
的函数所构成的完备空间中,埃尔米特多项式序列构成一组基。其中的内积定义如下:
埃尔米特微分方程
概率论中的埃尔米特多项式是以下微分方程的解:
方程的的边界条件为: 应在无穷远处有界。
应在无穷远处有界。
其中 是这个方程的本征值,是一个常数。要满足上述边界条件,应取
是这个方程的本征值,是一个常数。要满足上述边界条件,应取 ∈
∈ 。对于一个特定的本征值
。对于一个特定的本征值 ,对应着一个特定的本征函数解,即
,对应着一个特定的本征函数解,即 。
。
而物理学中的埃尔米特多项式则是以下微分方程的解:
其本征值同样为 ∈
∈ ,对应的本征函数解为
,对应的本征函数解为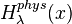 。
。
以上两个微分方程都称为埃尔米特方程。
from:http://blog.csdn.net/pipisorry/article/details/49366047
ref:mathworld Hermite Polynomial
wikipedia 埃尔米特多项式
数值分析:Hermite多项式的更多相关文章
- 数值计算方法实验之Hermite 多项式插值 (Python 代码)
一.实验目的 在已知f(x),x∈[a,b]的表达式,但函数值不便计算,或不知f(x),x∈[a,b]而又需要给出其在[a,b]上的值时,按插值原则f(xi)= yi(i= 0,1…….,n)求出简单 ...
- Hermite WENO 重构格式
Hermite WENO 单元重构 本文主要介绍采用 Hermite WENO 重构方法作为斜率限制器应用于二维或高维单元中. 1.简介[1] ENO格式最早由 Harten 等[2]提出,ENO格式 ...
- Matlab插值函数
x=0:2*pi; y=sin(x); xx=0:0.5:2*pi; %interp1对sin函数进行分段线性插值,调用interp1的时候,默认的是分段线性插值 y1=interp1(x,y,xx) ...
- Line Search and Quasi-Newton Methods 线性搜索与拟牛顿法
Gradient Descent 机器学习中很多模型的参数估计都要用到优化算法,梯度下降是其中最简单也用得最多的优化算法之一.梯度下降(Gradient Descent)[3]也被称之为最快梯度(St ...
- Line Search and Quasi-Newton Methods
Gradient Descent 机器学习中很多模型的参数估计都要用到优化算法,梯度下降是其中最简单也用得最多的优化算法之一.梯度下降(Gradient Descent)[3]也被称之为最快梯度(St ...
- 基于 Mathematica 的机器人仿真环境(机械臂篇)[转]
完美的教程,没有之一,收藏学习. 目的 本文手把手教你在 Mathematica 软件中搭建机器人的仿真环境,具体包括以下内容(所使用的版本是 Mathematica 11.1,更早的版本可能缺少某些 ...
- Image Processing and Analysis_8_Edge Detection:The Design and Use of Steerable Filters——1991
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:Finding Edges and Lines in Images by Canny——1983
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Java实现 蓝桥杯VIP 算法训练 非递归(暴力)
试题 算法训练 非递归 问题描述 当x>1时,Hermite多项式的定义见第二版教材125页.用户输入x和n,试编写"非递归"函数,输出对应的Hermite多项式的值.其中x ...
随机推荐
- 使用PHP脚本远程部署git项目
准备工作: 1.coding.net创建私有项目 2.安装了Web服务 Git服务的服务器 服务器端: 1.nginx.php-fpm统一用www用户 www 目录,这个可以通过修改配置文件实现. [ ...
- form submit提交
form内控件参数自动添加到url后,而自定义的url参数则不能添加到url后 $('#fm').form('submit', { url: 'Data/Diary.ashx?dt=' + new D ...
- 初识Redis系列之一:简单介绍
一:Redis是什么? Redis全称:REmote DIctionary Server(Redis) .Redis是一个由Salvatore Sanfilippo写的key-value存储系统,AN ...
- 使用redis做缓存
redis常本用来作为缓存服务器.缓存的好处是减少服务器的压力,数据查询速度快.解决数据响应慢的问题. 添加缓存:只用redis的Hash数据类型添加缓存. 例如:需要在查询的业务功能中,添加缓存 1 ...
- 学习ASP.NET Core Razor 编程系列七——修改列表页面
学习ASP.NET Core Razor 编程系列目录 学习ASP.NET Core Razor 编程系列一 学习ASP.NET Core Razor 编程系列二——添加一个实体 学习ASP.NET ...
- MeshCollider双面化脚本
由于MeshCollider组件可以挂载多个,所以不需要Mesh重新合并了. 除了反转法线还需要反转所有三角面的顺序 脚本如下: using System.Collections; using Sys ...
- python笔记七(递归函数)
在介绍递归函数之前,我们先介绍以下递归函数的使用有以下特征: 1.递归函数就是函数在函数体内部调用本身 2.递归函数的运算规模要不断减小,这样才是可以运算的 3.递归的层数不要超过999,因为函数调用 ...
- 进程间通信——XSI IPC之消息队列
进程间通信XSI IPC有3种:消息队列.共享内存.信号量.它们之间有很多相似之处,但也有各自的特殊的地方.消息队列作为其中比较简单的一种,它会有些什么东西呢,来一起探讨探讨.. 消息队列结构 消息队 ...
- Jmeter(七)_if控制器+循环控制器+计数器控制接口分支
最近查阅了一下网上关于if控制器的文章,大同小异,几乎找不到原创,于是决定自己写一篇 下午测试接口,遇到了一个审核的流程.逻辑很简单,就是审核不通过之后返回去继续修改再提交,然后再审核,直到通过为止. ...
- 分布式服务框架Dubbo
随着互联网的发展,网站应用的规模不断扩大,常规的垂直应用架构已无法应对,分布式服务架构以及流动计算架构势在必行,亟需一个治理系统确保架构有条不紊的演进. 单一应用架构 当网站流量很小时,只需一个应用, ...