剑指Offer 7. 斐波那契数列 （递归）

题目描述

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。

n<=39

题目地址

https://www.nowcoder.com/practice/c6c7742f5ba7442aada113136ddea0c3?tpId=13&tqId=11160&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

思路

斐波那契数列公式为：

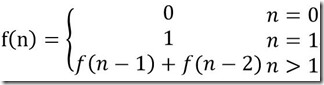
这道题递归很好写，但是存在很严重的效率问题。我们以求解f(10)为例类分析递归的求解过程。想求f(10)，需要先求得f(9)和f(8)。同样，想求得f(9)，需要先求的f(8)和f(7)....我们可以用树形结构来表示这种依赖关系，如下图所示：

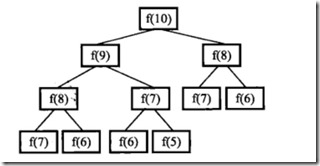
我们不难发现在这棵树中有很多结点是重复的，而且重复的结点数会随着n的增加而急剧增加，这意味计算量会随着n的增加而急剧增大。事实上，递归方法计算的时间复杂度是以n的指数的方式递增的。

所以，使用简单的循环方法来实现。

Python

# -*- coding:utf-8 -*-
class Solution:
    def Fibonacci(self, n):
        # write code here
        if n <= 1:
            return n
        a, b = 0,1
        for i in range(1,n):
            c = a + b
            a, b = b, c
        return c

if __name__ == '__main__':
    result = Solution().Fibonacci(6)
    print(result)